因果之间求发散
——例谈初中几何解题实践中发散思维的培养
江苏省如皋市高新区实验初中 程红卫
因果之间求发散
——例谈初中几何解题实践中发散思维的培养
江苏省如皋市高新区实验初中 程红卫
发散思维也叫作求异思维,是通过对信息的了解与分析,向着不同的方向探索多样化解决问题途径的思维过程,从而开拓学生的思路、培养学生思维的灵活性与变通性,在创造性思维中占有重要地位。初中数学中的几何教学,是培养学生发散思维的良好载体,在不断向外扩展的过程帮助学生在尝试摸索、反复变通中锻炼数学思维能力。
一、执因求果,在一题多解中培养发散兴趣
在初中数学几何解题实践中,学生思维僵化、循规蹈矩且缺乏活力是培养发散思维的主要障碍,因此激发学生对于新方法的认知热情、对新思路的探究欲望,就成为培养发散思维的首要环节。一题多解通过启发学生依据已知条件,从不同角度、不同途径解答同一道数学问题,从而多方面地获取该问题的正确结论,能够让学生的思维在各种新颖思路逐一展现的过程中,变得活跃起来;同时,在执因求果的多样化解答中,会促动学生进行主动交流、积极合作,在个体智慧的碰撞中得到各知识点之间的有效整合。
如在进行“添加辅助线”这一专项练习指导过程中,教师出示下题:
如图①,在四边形ABCD中,已知∠A=60°、
∠B=∠D=90°,BC=2、CD=3,求AB的长度。
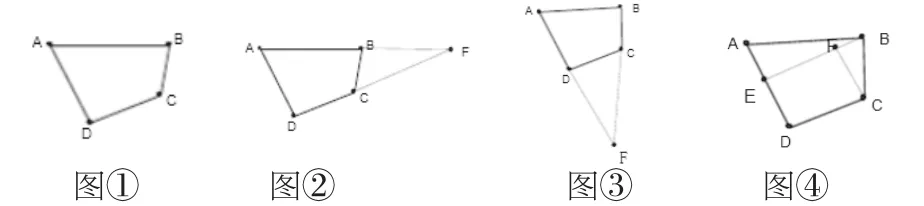
通过组织学生分组讨论和集体汇报,学生从不同角度进行了思考,得出如下多种解法:
解法一:如图②,延长AB、CD交于F;解法二:如图③,延长AD、BC交于F;解法三:如图④,分别过点B、C作BE⊥AD、CF⊥BE……随着解法越来越多,学生的热情愈发高涨,在一题多解中唤起强烈的发散兴趣,加深了有效添加辅助线这一几何解题策略的认知水平。
二、倒果为因,在角度转换中拓展发散思路
培养学生的发散思维,可以通过“反向推理”、“倒过来想”等倒果为因的举措,实现正向思维与逆向思维之间的互补,不但促进了学生几何解题策略的灵活性,更因为思维的双向互通,促进他们对于几何相关概念、定理以及公式的全面理解,形成完整、立体的知识印记。
如在指导学生解答下题时,教师就采用了逆向思考的方式拓展学生的发散思路:如右图(图⑤),一张长方形纸片ABCD,沿对角线AC把△ACD翻至△ACD',AD'与BC相交于点E,判断△AEC的形状并说明理由。
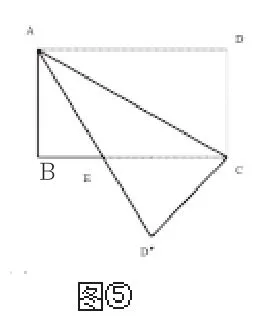
通过教师启发,学生倒果为因展开思考:如果△AEC是等腰三角形,则∠EAC=∠ECA即可,而△ACD'是△ACD沿AC翻折的,可知∠DAC=∠EAC,同长方形纸片ABCD可得AD∥BC,则有∠DAC=∠ECA,所以∠EAC=∠ECA,△AEC为等腰三角形;如果是等腰直角三角形,∠AEC=∠ABE+∠BAE,而∠ABE=90°,∠AEC不可能是90°,所以不可能是等腰直角三角形;等边三角形呢?条件不成立。通过这样的梳理,帮助学生逆向思想理顺了思路。
三、知果索因,在变式引申中提升发散能力
变式练习是数学教学中不可或缺的组成部分,是学生巩固既有认知、锻炼实践能力的重要途径,对于提升发散能力更是具有积极的推动作用。通过对同一类型的题目进行引申和变换,变化其非本质特征而保留本质特征,让学生从不同的层面和不同的角度知果索因,围绕着其中“变”与“不变”展开分析和思考。教师可以改变题目的条件、替换题目的结论以及转换题目的情境等多种变式方法,引导学生在反复探究中深化对于基本知识的理解和基础技能的掌握,使得他们的发散能力得以有效提升。
如教师在指导解答下题时,运用了变式的方法提升学生发散思维能力:如下图(图⑥),已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG。求证:EG=CG。
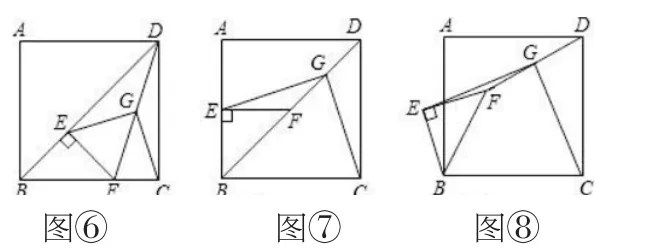
变式一:将图⑥中△BEF绕B点逆时针旋转45°,如图⑦所示,取DF中点G,连接EG,CG。EG=CG的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
变式二:将图⑥中△BEF绕B点旋转任意角度,如图⑧所示,再连接相应的线段,问原结论是否仍然成立?通过观察你还能得出什么结论。
四、收因结果,在梳理建构中巩固发散成果
归纳和梳理是学生数学学习所必备的一项基本素质,也是他们实现自我建构的必经之路,通过将分散、零碎的知识点进行分类和总结,从而形成一套适合他们个体使用的知识网络。这不但是对于几何解题练习中发散思维成果的巩固,更为他们后继数学学习提供了可持续发展的基石。
如在“证明两条直线互相平行”的复习整理中,教师指导学生展开回顾,将相关内容整理如下:①垂直于同一直线的两条直线平行;②同位角相等(或内错角相等,或同旁内角互补),两条直线平行;③平行四边形的对边平行;④三角形的中位线平行于第三边;⑤梯形的中位线平行于梯形的两底;⑥平行于同一直线的两条直线平行……帮助学生在解答此类问题时,做到心中有底、脑中有法。
发散性思维以其积极性、求异性、广阔性、联想性等,对于初中几何教学效率的提升和效果的彰显具有重要意义,每一个初中数学教学工作者都应当给予足够的重视,以此与诸君共勉。

