Ω-凸Fuzzy集

傅小波

(无锡职业技术学院 基础部,江苏 无锡 214121)



Ω-凸Fuzzy集

傅小波

(无锡职业技术学院 基础部,江苏 无锡 214121)

给定一个参数集，将Ω-模糊集与凸集相结合，提出了一种新的Ω-凸Fuzzy集，并研究了Ω-凸Fuzzy集的一些基本性质。

Ω-模糊集；Ω-凸Fuzzy集

自1965年L.A.Zadeh 在文献[1]中首次提出Fuzzy集和凸Fuzzy 集概念以来, Fuzzy集的思想和方法已经被广泛应用于各个领域，极大地促进了有关不确定性信息问题的研究和发展。随后众多学者对凸Fuzzy集作了进一步的研究, 获得了许多有意义的结果[2-10]。本文在上述研究工作的基础上，将文献[11]中的Ω-模糊集的思想应用于凸集，提出了更为广泛的Ω-凸Fuzzy集。

1 预备知识

定义1.1[1]设X为论域,A⊂X,若∀x,y∈A,∀λ∈[0,1],有λx+(1-λ)y∈A，则称A为凸集。

定义1.1[1]设X为论域，映射A:X→[0,1]称为X的模糊集。

定义1.1[11]设X为论域，Ω为非空给定集合,映射A:X×Ω→[0,1]称为X的Ω-模糊集。

论域X上的全体Fuzzy集记作Ω-F(X)。

2 Ω-凸Fuzzy集

定义3.1 设A∈Ω-F(X),∀x,y∈X, ∀δ∈Ω,∀λ∈[0,1]，若

则称A为Ω-凸Fuzzy集。

定理3.1 若A,B是Ω-凸Fuzzy集，则A∩B是Ω-凸Fuzzy集。

证明 ∀x,y∈X,∀δ∈Ω,∀λ∈[0,1]，若A,B是Ω-凸Fuzzy集，则有

(A∩B)(λx+(1-λ)y,δ)

=A(λx+(1-λ)y,δ)∧B(λx+(1-λ)y,δ)

≥(A(x,δ)∧A(y,δ)∧(B(x,δ)∧B(y,δ))

=(A(x,δ)∧B(x,δ)∧(A(y,δ)∧B(y,δ))

=(A∩B)(x,δ)∧(A∩B)(y,δ),

从而可知，A∩B是Ω-凸Fuzzy集。

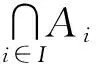
定义3.2 设Α∈Ω-F(X)是Ω-凸Fuzzy集，若∀α∈[0,1],

则称Aα为Α的关于Ω的水平上截集。

定义3.3 设Α∈Ω-F(X)是Ω-凸Fuzzy集，若∀α∈[0,1],

则称Aα>为Α的关于Ω的水平上截集。

定理3.3 设Α(∈Ω-F(X))是Ω-凸Fuzzy集，当且仅当Aα为凸集。

证明 “⟹” 若Α是Ω-凸Fuzzy集，则∀α∈[0,1],∀x,y∈Aα,因为A(x,δ)≥α,A(y,δ)≥α.从而∀λ∈[0,1],有

所以λx+(1-λ)y∈Aα,即Aα为凸集。

“⟸” 若Α不是Ω-凸Fuzzy集，则∃x0,y0∈X,使

令α0∈[0,1]满足下列条件：

则A(x,δ)≥α0,A(y,δ)≥α0,且A(λx0+(1-λ)y0,δ)<α0,从而有α0∈[0,1],x0,y0∈Aα0,且λx0+(1-λ)y0∉Aα0.又Aα0是凸集,于是有λx0+(1-λ)y0∈Aα0,与λx0+(1-λ)y0∉Aα0矛盾。所以Α是Ω-凸Fuzzy集。

类似与定理3.3的证明，可得下列定理3.4。

定理3.4 设Α(∈Ω-F(X))是Ω-凸Fuzzy集，当且仅当Aα>为凸集。

定理3.5 设Α∈Ω-F(X)，若∃α∈(0,1)，使A(αx+(1-α)y,δ)≥A(y,δ),∀x,y∈X,则B={α∈[0,1]|A(αx+(1-α)y,δ)≥A(x,δ)∧A(y,δ),∀x,y∈X}在[0,1]上是稠密的。

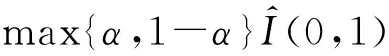
设α′=αβ1+(1-α)β2，则

α′x+(1-α′)y

=[αβ1+(1-α)β2]x+[1-αβ1-(1-α)β2]y

=α[β1x+(1-β1)y]+(1-α)[β2x+(1-β2)y]

于是，

A(α′x+(1-α′)y,δ)

=A{α[β1x+(1-β1)y]+(1-α)[β2x+(1-β2)y],δ}

≥A[β1x+(1-β1)y,δ]∧A[β2x+(1-β2)y,δ]

≥(A(x,δ)∧A(y,δ))∧(A(x,δ)∧A(y,δ))

=A(x,δ)∧A(y,δ),

因此，α′∈B.

1) 若α′≥α0，则有0≤β2≤α2≤α1≤α′≤1，从而α′-β2≥α1-α2，又因为

α′-β2

=αβ1+(1-α)β2-β2

=α(β1-β2)

<α1-α2，

与α′-β2≥α1-α2矛盾。

2)若α′<α0，则有0≤α′≤α2≤α1≤β1≤1，从而β1-α′≥α1-α2，又因为

β1-α′=β1-(αβ1+(1-α)β2)

=(1-α)(β1-β2)<α1-α2，

与α′-β2≥α1-α2矛盾。

综上所述，B在[0,1]上是稠密的。

定义3.3 设Α∈Ω-F(X)， ∀ε>0, ∃δ>0，若∀y∈X且∥y-x∥<σ,有

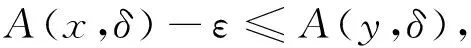
则称Α关于Ω是下半连续的。

定理3.6 设Α∈Ω-F(X)关于Ω是下半连续的，若∃α∈(0,1),∀x,y∈X,∀δ∈Ω，有

则Α是Ω-凸Fuzzy集。

证明 若Α不是Ω-凸Fuzzy集，则∃x,y∈X,α′∈(0,1)，使

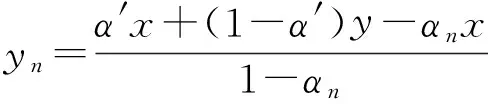
因为Α关于Ω是下半连续的，且yn→y(n→∞)，从而可知，

其中N>0，所以

A(α′x+(1-α′)y,δ)

=A[(1-αn)yn+αnx,δ]

≥A(yn,δ)∧A(x,δ)

≥A(E(y)-ε,δ)∧A(x,δ),

由ε的任意性可知，

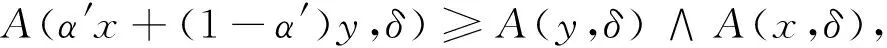
与A(α′x+(1-α′)y,δ)

综上所述，Α是Ω-凸Fuzzy集。

[1] Zadeh L A.Fuzzy sets[J].Information and Control, 1965, 8:338-353.

[2] Liu Y M．Some properties of convex fuzzy sets[J].Journal of Mathematical Analysis and Applications,1965,111(1): 119-129．

[3] Smon S. The sequence spacesl(pv)andm(pv)[J]. Proceedings of the London Mathematical Society,1965, 8(3): 422-436.

[4] 方锦暄．Fuzzy凸集的分离定理[J].科学通报, 1983,28(21): 1289-1291．

[5] Youness E A．E-convex sets，E-convex functions，and E -convex programming[J].Journal of Optimization Theory and Applications, 1999, 102(2): 439-450.

[6] Yang X M．On E-convex set，E-convex functions，and E -convex programming[J].Journal of Optimization Theory and Applications,2001,109(3): 699-704.

[7] Jian J B．Incorrect result for E-convex functions，and E- convex programming[J].Mathematical Research and Exposition,2003,23(3): 461-466．

[8] 鞠红梅,袁学海,陈图云．凸模糊子集的再定义[J].模糊系统与数学,2001,15(1): 68- 70．

[9] 顾惠,廖祖华．广义Fuzzy凸集[J].模糊系统与数学， 2004,18: 153-156．

[10] Gu H，Liao Z H．(∈,∈∨q(λ,μ))-convex fuzzy set[J].模糊系统与数学,2007,21(1): 92 - 96．

[11] Young B J, Kyung H K, Zhang Q. On Ω-fuzzy ideals of BCK/BCI algebras[J]．The Journal of Fuzzy Mathematics, 2001, 9(1):173-180.

责任编辑 俞 林

Ω-Invex Fuzzy Set

FUXiaobo

(Department of Basic Courses, Wuxi Institute of Technology, Wuxi 214121， China)

LetΩbe a parameter set.By combining theΩ- fuzzy sets and the invex set, the concepts of invexΩ-fuzzy set is proposed, and some related properties are studied.

Ω- Fuzzy Sets；Ω- Invex fuzzy sets

2016-09-01

傅小波(1980— )，男，江苏无锡人，讲师，研究方向：模糊代数，人工智能。

10.13750/j.cnki.issn.1671-7880.2016.06.017

O 15

A

1671-7880(2016)06-0061-03