多视角 真本质——2016年浙江省数学高考理科试题第16题解读*

●庄迁福

(温州第二高级中学 浙江温州 325000)



多视角 真本质
——2016年浙江省数学高考理科试题第16题解读*

●庄迁福

(温州第二高级中学 浙江温州 325000)

高考“考什么，怎么考”直接影响了教学中“教什么，怎么教”.文章以2016年浙江省数学高考理科试题第16题为例，探寻出题者的意图，分析考生答题情况，多视角探究解三角形常见的解法，绘制成解三角的思维网图，多方位关注学生的发展.

解三角形；视角；边角转化；齐次式

解三角形是高考的重要考点之一，也是连接平面图形与代数运算的一个纽带.近几年，浙江省数学高考文、理科多以解答题的形式出题，主要考查三角形边角转换与三角化简等知识与方法，难度不大，是考生必争之分，怎样做得好对考生意义重大[1]．

题目 在△ABC中，内角A，B，C所对的边分别是a,b,c，已知b+c=2acosB.

1)证明：A=2B；

(2016年浙江省数学高考理科试题第16题)

命题组给出的参考答案如下：

1)证法1 由正弦定理得

sinB+sinC=2sinAcosB，

从而 sinB+sinC= sinB+sin(A+B)=

sinB+sinAcosB+cosAsinB，

于是

sinB=sin(A-B),

因此，A=π(舍去)或A=2B，故A=2B.

得

sinC=cosB.

又B,C∈(0,π)，于是

解得

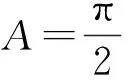
1 命题思路探寻

本题紧扣高考大纲要求：能够应用正弦定理、余弦定理实现三角形中边与角的转化.本题叙述简洁明了，条件中边角关系式朴实，让考生能很快上手，考查了借助定理转换边角关系、三角诱导公式与三角两角和差公式的应用.第1)小题以证明题的形式给出，注重推理能力的应用；第2)小题结合三角形面积，用角或边关系求角的值，化简过程中让考生充分感悟三角解题技巧的灵活性.

2 考生答题反馈

本题答题总体良好，表达基本规范，较多的学生运用解法1和证法1完成，反馈出考生解三角形的基本功扎实.第1)小题，学生思路明确，多以化边为角的方法完成，有的学生错用sinC=-sin(A+B)，也能根据结论进行检查修正；第2)小题，有些学生化简思路不明确，缠绕其中，越化越复杂，无法完成，有些学生三角转换中出现漏解情况.3 巧妙解题方法

解三角形以边角转换的灵活多变为特征，解题过程中常遇见学生方法单一，一遇到困难就无法完成的情况，需多视角去探寻边角关系，以三角形可解所需条件分析为本质，数形结合，不惧繁琐.

3.1 第1)小题的解题视角

视角1 角的变形

证法2 由已知得sinB+sinC=2sinAcosB，

右边2sinAcosB可拆解为

2sinAcosB= sin(A+B)+sin(A-B)=

sinC+sin(A-B),

从而

sinB=sin(A-B).

证法3 由已知得sinB+sinC=2sinAcosB，也可先寻找B,C之间的关系

sinB+sinC= 2sinAcosB=2sin(B+C)cosB=

2sinBcosBcosC+2cos2BsinC=

sin2BcosC+cos2BsinC+sinC=

sin(2B+C)+sinC,

从而

sinB=sin(2B+C).

因为B≠2B+C，所以

B+2B+C=π，

故

A=2B.

点评 证法2巧妙运用了2A=(A+B)+(A-B)，2B=(A+B)-(A-B)，这也是三角恒等变形中拆角的一种方法.证法3利用三角形中A+B+C=π之间的关系，成功将B与C的关系转化为A与B之间的关系.

视角2 角的构造

从而

sin2B=sinA，

于是

A=2B.

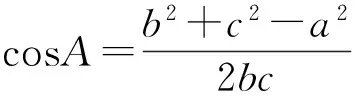
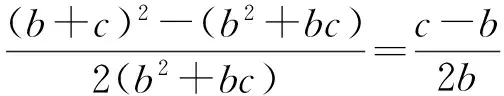
从而

cos2B=cosA，

解得

A=2B.

点评 上述2种证法从结论出发，用分析法得到sin2B=sinA或cos2B=cosA，再从边角关系进行构造.

视角3 线的添加

证法6 如图1，过点C作CO⊥AB于点O，延长BA使得OD=OB，联结CD，易知CO是BD的中垂线，则∠B=∠D.又BO=acosB，从而

BD=2acosB.

对于b+c=2acosB，结合图形可知

AC+BA=BD=BA+AD，

从而

AC=AD，

于是

∠ACD=∠CDA,

因此∠CAB=∠ACD+∠CDA=2∠CDA=2∠B，

故

A=2B.

图1 图2

从而

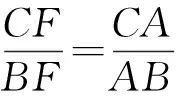
由角平分线定理可知，AF是角A的平分线，则∠CAF=∠FAB, ∠CAB=∠CAF+∠FAB=2∠B,故

A=2B.

点评 证法6将b+c=2acosB关系转化为折线段的关系，将代数式以直观的图像呈现，使边角关系更加清晰.证法7由A=2B联想到角平行线，将图形中角度关系用代数运算进行验证，体现了数形结合思想在解三角形中的运用.

3.2 第2)小题的解题视角

视角1 方程思想的运用

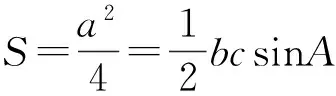
a2=2bcsinA.

将所有的边转化角A的关系，即

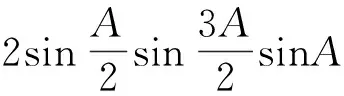
化简得

从而

sinA=2sinBsinC,

再化简成角A的关系式，即

sinA= 2sinBsin(A+B)=

sin2BsinA+2sin2BcosA=

sin2A-cos2A+cosA,

从而

(sinA-cosA)(sinA+cosA-1)=0，

即

解得

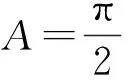
点评 上述2种解法都是将等式化简为关于角A的一个方程式或一个等式，从而求得自变量，显得更加自然，当然也可以其他角表示.解法2有助于sinC=cosB三角关系的理解，解法3避免了解法1中出现漏解的情况.

视角2 齐次式的计算

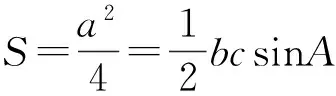
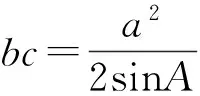
sinA+2sinAcosA-1,

下同解法3.

解法5 在解法1中利用cosB=sinC进行化简，也可用sinC=sin3B和sin3B=3cos2BsinB-sin3B进行化简，再通过齐次式转为正切计算，即

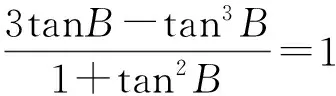
点评 三角形的余弦定理本身就是关于边长a,b,c的一个齐次式，是转为函数、方程或不等式求值或最值常用的桥梁之一.将“1”变形为“1=sin2A+cos2A”是三角计算常用的一个技巧.

视角3 同角的计算

(t2-1)(t2+2t-1)=0，

点评 本题中的三角可以确定角度，可构成一组相似的三角形，边长的比值可以确定.

4 教学思考启示

教学中应处理好学生“学什么，教师教什么，考试考什么”这3者的关系，教学过程中围绕着知识点，通过数学思想方法的领悟揭示数学的本质，既发展了学生的思维，又不失数学的工具性，增加应用意识.因此，要让学生参与到解题的探究过程中来，注重双基，积累归纳，感悟提升.

4.1 注重双基，形成网络

解三角所覆盖的知识点很多，所涉及的公式定理也很多，可以使知识点连成线，形成“三角化简一条线，边角转化一条线，向量具体一条线，基本不等式结合一条线”等，再由线构网[2]，让学生在解题过程中可进可退，提高信心与成功率.

4.2 积累归纳，画龙点睛

解三角常见的问题有2个：一是计算过程出错，需要学生积累易错点，比如三角化简的符号出错，错用cosA=cos(B+C)，不具备正弦定理转化条件，如将a2=b+c转化为sin2A=sinB+sinC；二是方法使用不当、化简不出或者没有思路，需要学生对解题进行归纳，例如已知角A与边a，求b+c范围的问题，学生常用余弦定理结合基本不等式的思路完成，只求一半的范围，实需再考虑b+c>a，同时引进将边化为角的方法，用正弦定理转为角B或C的函数求范围，教学中可归纳为一组对边对角类型.

4.3 感悟提升，灵活转化

解题教学中，应该重视学生的感悟，在完成某一种方法的时候，既要总结、谈感受、点评，又要鼓励学生去变式、去多解、去特殊到一般，达到“解一题,会一类”的目标，将演绎推理与数学思想方法运用于解题的每一环节.

[1] 杨建三．理解基础知识 掌握基本方法 运用解题策略——2010年浙江省数学高考文科试题第18题解读[J]．中学教研(数学)，2010(8)：20-21.

[2] 蔡明．2010年浙江省数学高考理科试题第18题解读[J]．中学教研(数学)，2010(8)：12-13.

�2016-06-16；

2016-07-20

庄迁福(1986-)，男，浙江温州人，中学一级教师.研究方向：数学教育.

O124.1

A

1003-6407(2016)11-37-04