貌离神合 同源切线——全国数学高考Ⅰ卷文、理科第20题评析与思考*

●洪剑林

(潮安区教育局教研室 广东潮州 515600)



貌离神合 同源切线
——全国数学高考Ⅰ卷文、理科第20题评析与思考*

●洪剑林

(潮安区教育局教研室 广东潮州 515600)

文章分别对2016年全国I卷数学文、理科第20题进行评析、探源、推广.2道试题貌离神合、同源于圆锥曲线的切线问题，并思考数学教学的有效性,如何构建知识体系与形成思想方法体系.

全国卷;高考题;评析;教学;类比探究

1 理科试题评析

1.1 试题

例1 如图1,设圆x2+y2+2x-15=0的圆心为A,直线l过点B(1,0)且与x轴不重合,l交⊙A于点C,D,过点B作AC的平行线交AD于点E.

1)证明：|EA|+|EB|为定值,并写出点E的轨迹方程；

2)设点E的轨迹为曲线C1,直线l交C1于点M,N,过点B且与l垂直的直线与⊙A交于点P,Q,求四边形MPNQ面积的取值范围.

(2016年全国数学高考理科I卷第20题)

1.2 解法

1)证明 ⊙A的方程为

(x+1)2+y2=16,

圆心A(-1,0),半径AC=AD=4,从而

∠ACB=∠ADB.

由已知得BE∥AC,从而

∠ACB=∠EBD,

进而

∠ADB=∠EBD,

得

EB=ED,

故

|EA|+|EB|=|AD|=4.

评注 从问题设置分2步来看,思路单一但起点低,命题人应是有意放低门槛,带有提示之意,也可以避免走弯路.

图1 图2

2)解法1 如图2，设直线l的方程为

x=my+1,

(3m2+4)y2+6my-9=0,

从而

直线PQ的方程为

y=-m(x-1),

且P(x3,y3),Q(x4,y4),由

得

(m2+1)x2+(2-2m2)x+m2-15=0,

从而

四边形MPNQ的面积为

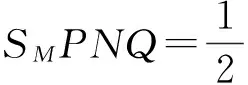
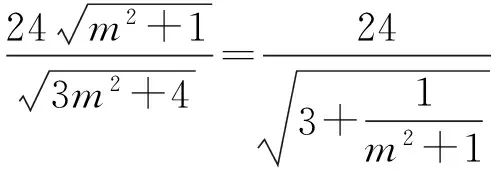
又m2≥0,得

即

从而

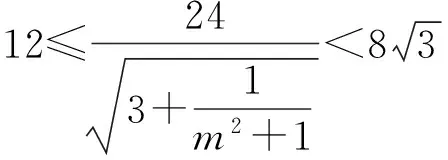
评注 本解法中直线方程不采用斜截式,避免斜率是否存在的讨论,而且直线l的方程为x=my+1与直线PQ的方程为y=-m(x-1)，这2个方程式使弦长公式的计算简洁得多.

解法2 设BN的倾斜角为α(其中0<α<π),而|NA|+|NB|=4,|AB|=2,在△NAB中,由余弦定理得|NA|2=|NB|2+|AB|2-2|NB|·|AB|cos(π-α),从而 (4-|NB|)2=|NB|2+4+4|NB|cosα,

得

同理可得

于是

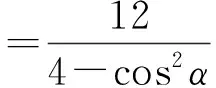
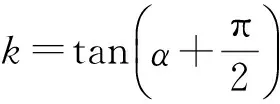
直线PQ的方程为

y=k(x-1),

即

kx-y-k=0,

故圆心A(-1,0)到弦PQ的距离为

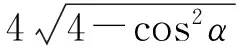
四边形MPNQ的面积为

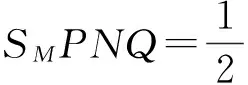
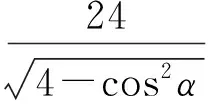
由0≤cos2α<1,得

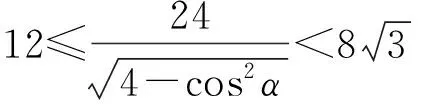
评注 本解法利用焦距与二焦半径围成的△NAB,结合余弦定理求得焦半径NB、过焦点的弦长MN,在圆中利用半径与弦特有的直角三角形,求得弦长,进而运用三角函数的有界求取值范围,取得范围的求解较解法1简单、快捷.

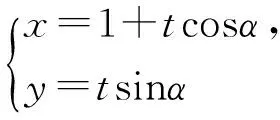
(3+sin2α)t2+6t·cosα-9=0.

设方程的2个解为t1,t2,则

由参数t的几何意义得

|MN|= |t1-t2|=

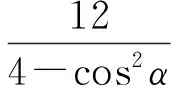
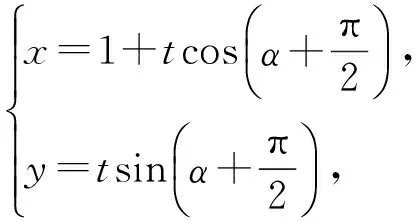
即

代入圆方程x2+y2+2x-15=0得

t2-4tsinα-12=0.

设方程的2个解为t3,t4,则

t3+t4=4sinα,t3t4=-12,

由参数t的几何意义得

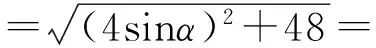
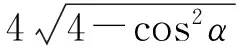
下同解法2.

评注 解法3运用直线的参数方程,利用参数t的几何意义直接求解,运算更为简洁、明了.

1.3 探源与点评

图3

如图3，试题中记BD的中点为K,结合椭圆的光学性质易得EK为椭圆上点E处的切线.显然该题利用椭圆上任一点切线的几何作法逆向而命制.

本题解答从几何证明入手,考查逻辑推理能力,凸显解析几何的学科本质.解析几何首先是几何,“代数”只是我们解决几何问题时用到的工具.第2)小题以直线与圆、直线与椭圆为背景,与几何图形面积的最值相结合,考查学生对圆锥曲线知识的掌握,也与函数、方程、不等式等主干知识链接.近年来全国卷试题中求四边形面积取值范围的很多.

试题给考生平易近人之感,但却有很好的区分度,梯度明显,需要考生有较强的数学能力,通过题海战术并不能赢得高分.

2 文科试题评析

2.1 试题

例2 在直角坐标系xOy中,直线l:y=t(其中t≠0)交y轴于点M,交抛物线C：y2=2px(其中p>0)于点P,且点M关于点P的对称点为N,联结ON并延长交C于点H.

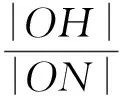
2)除点H以外,直线MH与C是否有其他公共点?说明理由.

(2016年全国数学高考文科I卷试题第20题)

2.2 解法

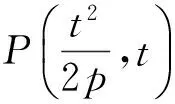
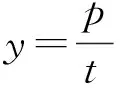
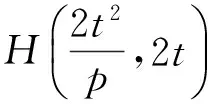
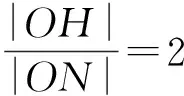
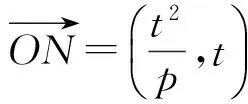
即

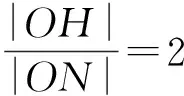
2)直线MH与抛物线C除H外没有其他公共点.理由如下:

解法1 (判别式法)由第1)小题知直线MH的斜率为

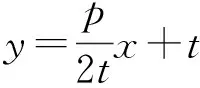
代入抛物线方程y2=2px得

y2-4ty+4t2=0,

从而Δ=0,方程只有1个解,故直线MH与C只有1个公共点,除H外没有其他公共点.

解法2 (导数法)由第1)小题知直线HM的斜率为

在x轴上方抛物线弧方程为

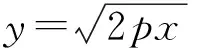
求导得

故抛物线在点H处的切线斜率为

可知直线HM恰好是抛物线的切线.故判断成立.

2.3 探源与点评

该题利用阿基米德三角形的这个性质命制,而且将直线特殊为过原点,使求解代数运算简单得多.阿基米德三角形有很多有趣的性质,近年来全国各地高考解析几何题以阿基米德三角形为背景命制的很多.

该题背景经典、意境深广,设计平凡又简洁,解法常规而多样,全面考查解析几何的基本思想与方法,常规中考能力,平实中考思维,是文科考生熟悉的题型.同时,也是一道值得研究的好题,深入思考,内涵丰富,提供了一种求作圆锥曲线切线的几何方法.

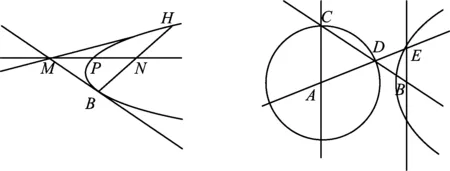
图4 图5

3 联想探究,获得新知

3.1 类比探究理科题

由理科题目出发,把点B移到⊙A外部,同理可得：

问题1 如图5,已知⊙A及圆外一点B,直线l过点B且与直线AB不重合,l交⊙A于点C,D,过点B作AC的平行线交AD于点E,则点E的轨迹是以AB的中点为中心、A，B为焦点、以⊙A的半径为实轴长的双曲线的一支(除去与直线AB的交点).

问题2 在问题1的条件下,记BD的中点为K,易得直线EK为双曲线上点E的切线.

3.2 类比探究文科题

由文科题目出发,我们可以利用y轴或顶点的切线,轻松地作出抛物线上任一点的切线,并将其推广到圆、椭圆和双曲线[2].

定理1 如图6,已知O是抛物线C：y2=2px(其中p>0)的顶点,过抛物线上任意一点P(不同于点O)作PQ⊥y轴于点Q.记OQ的中点为M,则PM是抛物线上点P的切线.

注 定理1的证明与例2基本一致,在此不再赘述.根据定理1,可以作抛物线上不同于点O的任一点P的切线,而点O处的切线是y轴,这样我们利用y轴可以作抛物线上任一点的切线.

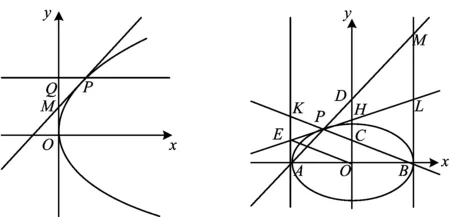
图6 图7

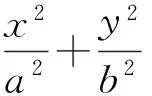
即

解得

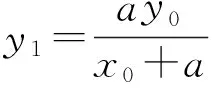
即

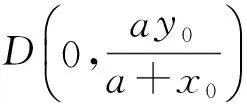
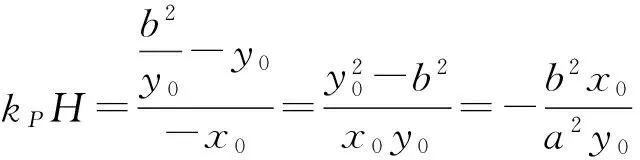
命题得证.

注 由图7可知,点E为AK的中点,点L为BM的中点,而且点E,AP的中点与椭圆中心3个点共线.根据定理2,利用y轴可以作椭圆上不是顶点的任一点P的切线,左、右顶点处切线平行于y轴,上、下顶点处切线垂直于y轴,这样我们利用y轴可以作椭圆上任一点的切线.圆可由椭圆变换得到,显然此定理在圆上成立.

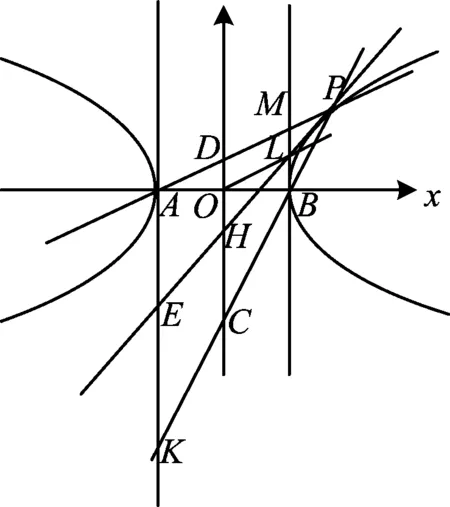
图8

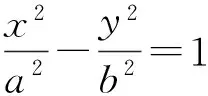
注 定理3的证明方法与定理2相似,此处不再说明.由图8可知,点E为AK的中点,点L为BM的中点,而且点L、BP的中点与双曲线中心3个点共线.根据定理3,利用y轴可以作双曲线上任一点P的切线.

4 教学思考

题海茫茫,教材是岸.学生接触最早、最多的是教材,不管是高一、高二的教学,还是高三的备考复习教学,教师都应当重视教材的示范作用.教材应当成为学生构建知识体系的主阵地、形成数学思想方法体系的主阵地,从而培养数学素养.

4.1 如何构建知识体系

重视基础,回归课本,纵横整合课本,突出数学基本概念和基本原理的教学,有效构建知识体系.在学生按照教材内容顺序掌握知识的基础上,指导学生对课本进行专题整理、深挖与研究.

学生在课本范围内开展研究,高三复习可扩大范围到近年高考题,可操作性强,效果好.通过不同内容的联系,强调对命题推广、特殊化、类比等,学生数学地思考、研究课本,形成结构化的知识体系.

4.2 如何形成数学思想方法体系

突出数学思想方法教学,注重提高学生数学思维能力.函数与曲线是贯穿中学数学的一对孪生姐妹,解析几何用的是代数方法研究几何问题.如圆锥曲线在纯几何研究的基础上,要求学生感受、形成“数形结合”的基本思想,更要明确“坐标方法”下有那些工具[3]：

1)用代数方法研究直线、圆锥曲线:用数、代数式、方程表出点、距离、直线、圆锥曲线,用数及其运算为工具进行讨论,把结果给予几何解释使问题得以解决.

2)用向量来研究几何:用向量表示出问题中的点、线,用向量及其运算为工具,进行向量计算而得到结果,把结果给予几何解释使问题得以解决.

3)用微分方法研究平面曲线:函数对应曲线,导数就是曲线切线的斜率,用导数为工具,用分析法研究曲线.

4)用三角函数解三角形.

多种方法就有了多种选择,也就可以多角度地开展研究,开阔了思维空间.“代数方法研究圆锥曲线”是最熟悉的,应当常常思考“能否用向量法研究圆锥曲线”“能否用综合法研究圆锥曲线”……以上4个工具在前面的研究中都有用武之地.利用不同内容的内在联系,使之呈现异曲同工之妙,从而提高学生对数学思想方法的整体认识.

[1] 姚汉兵,王怀明.立足课本,在制高点思考[J].中学数学研究：上半月,2013(11):22-24.

[2] 张翼飞.圆的一个优美性质在圆锥曲线中的推广及应用[J].中学数学研究：上半月,2012(2):26.

[3] 中学数学室.高中数学[M].北京：人民教育出版社,2007.

�2016-06-15；

2016-07-15

洪剑林(1976-),男,广东潮州人,中学数学高级教师.研究方向：数学教育.

O123.1

A

1003-6407(2016)11-20-05