结合Total-Bregman距离的模糊聚类算法*

超木日力格，于　剑+，朱　杰,2

1.北京交通大学 计算机与信息技术学院 交通数据分析与挖掘北京市重点实验室，北京 100044

2.中央司法警官学院 信息管理系，河北 保定 071000

结合Total-Bregman距离的模糊聚类算法*

超木日力格1，于剑1+，朱杰1,2

1.北京交通大学 计算机与信息技术学院 交通数据分析与挖掘北京市重点实验室，北京 100044

2.中央司法警官学院 信息管理系，河北 保定 071000

Chaomurilige,YU Jian,ZHU Jie.Fuzzy clustering algorithm based on Total-Bregman divergence.Journal of Frontiers of Computer Science and Technology,2016,10(2):220-229.

模糊C均值（fuzzy C-means,FCM）聚类算法是一种常用的基于目标函数最小化的聚类算法。目前已经提出了相当数量的聚类算法是对模糊C均值聚类算法的改进，例如AFCM算法、GK算法等。对最近发表的基于Bregman距离的模糊聚类算法进行了改进，通过在FCM模糊聚类框架中引入Total-Bregman距离提升了聚类算法的聚类性能。同时对基于Total-Bregman距离的模糊聚类算法的收敛性质进行了理论分析。实验部分对来自UCI数据库的几个数据集进行了聚类，证明了算法的有效性和收敛性。

聚类算法；模糊聚类；Total-Bregman距离

1　引言

近年来，随着网络和多媒体的蓬勃发展，收集到的海量文本信息、图像信息、视频信息、音频信息等数据使得人工处理这些数据变得越来越难。机器学习研究的崛起使得人们有可能通过机器学习的方式处理这些数据。机器学习研究中，聚类作为一种无监督学习方式，得到了来自各个领域研究者的关注。数据聚类算法在许多领域受到广泛应用，包括机器学习、数据挖掘、模式识别、图像分析和生物信息。在聚类算法的发展历程中，研究工作者们尝试从不同角度来描述聚类问题，并提出了许多基于不同理论且适用于不同应用的聚类算法[1]。

相对于有监督的分类问题，聚类是一种在没有任何先验信息的条件下将无标记数据进行归类的过程。对于聚类算法，迄今为止都没有一个学术界公认的定义。Everitt[2]于1974年给出了关于聚类的定义：一个类簇内的样例是相似的，不同类簇的样例是不相似的；一个类簇是测试空间中点的会聚，同一类簇的任意两个点间的距离小于不同类簇的任意两个点间的距离；类簇可以描述一个包含密度相对较高的点集的多维空间中的联通区域，它们借助包含密度相对较低的点集的区域与其他区域（类簇）相分离。由聚类算法的定义可知，聚类的关键问题是相似度或相异度的度量[3]，即怎样计算点（样例为测试空间中的一点）与点间的距离。只要定义了相似度或相异度的度量，就可以挖掘出数据的内在结构，为进一步的数据分析提供信息。因此，聚类结果直接依赖于相似度或相异度度量，对于模糊聚类算法亦是如此。

模糊集的概念由Zadeh于1965提出之后[4]，即成为软划分聚类有力的分析工具。软划分聚类算法中，数据可能同时属于若干个类，而其隶属于某个类的程度是根据隶属度来定义的。模糊C均值算法（fuzzy C-means,FCM）自Dunn在1973年提出[5-6]之后随即成为了应用最广、最灵活的一种模糊聚类算法，它是对硬C均值聚类算法的一种改进算法。之后为了克服FCM算法只对球形数据的聚类结果较为理想的缺点，Gustafson和Kessel等人将马氏距离引入模糊C均值聚类算法框架中，给出了GK模糊聚类算法[7-8]。该算法的优点在于，对非球形的簇，尤其是椭圆形的簇，聚类效果非常好。Yang等人在FCM模糊聚类算法的框架中引入高斯核，使得算法对于离群点和噪声更加鲁棒[9]。之后，Yang等人又在FCM算法的框架下结合类间离散度和类内紧致度提出了另一种模糊聚类算法[10]。2012年，Xiong等人提出，所有适用于FCM算法框架的距离表达均可由连续可微的凸函数导出。文章核心思想为，当且仅当距离为P2C-D距离（即Bregman距离）时，该距离适用于FCM聚类算法框架[11]。这类算法称之为基于Bregman距离的模糊聚类算法。

本文将Total-Bregman距离与FCM模糊聚类框架相结合，提出了结合模糊C均值聚类框架与Total-Bregman距离的模糊聚类算法，并证明了该算法的收敛性等性质。

本文组织结构如下：第2章重点回顾FCM算法；第3章重点介绍基于Bregman距离的模糊聚类算法；第4章介绍Total-Bregman距离和结合模糊C均值聚类框架与Total-Bregman距离的模糊聚类算法；最后给出一些实验结果，并展望未来的工作。

2　模糊C均值聚类算法

模糊C均值聚类算法由Dunn在1973年提出，目前在很多领域得到了广泛的应用。该聚类算法允许数据点同时属于两个甚至多个类，而每个数据点属于某个类的程度用隶属度进行约束，从而达到数据分类的目的。

首先，定义X数据集中第k个样本xk和第i个聚类中心vi之间的误差平方和（欧式距离）：

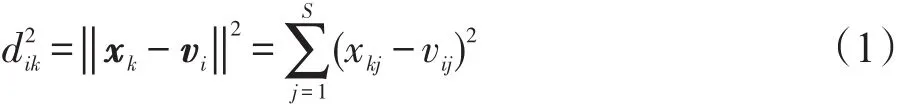
在FCM算法中，样本到聚类中心的距离是通过欧氏距离定义的。

Dunn对每个数据点与每个聚类中心的距离用其隶属度平方加权，得到类内加权平方和目标函数为：

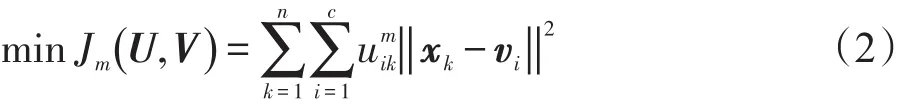
受限条件为：

式（2）中，m为模糊指数，用以控制聚类结果的模糊程度。将满足所有受限条件的矩阵集合记为：

通过使用拉格朗日乘数法，可以得到FCM算法的迭代公式如下：

模糊C均值聚类算法是一个简单的迭代过程，具体的实现框架如下：

算法1 FCM模糊聚类算法框架

上述算法也可以先初始化聚类中心，然后再执行迭代过程。不论采用何种方法，整个计算过程就是反复更新聚类中心和划分矩阵，因此这种方法又称为动态聚类或交替优化聚类法。

模糊C-均值算法是目前应用较广的一种聚类算法，但也存在着很多的问题。例如FCM算法需要事先确定数据集的分类数c；需要初始化聚类中心和加权指数m等。但与此相比，FCM聚类算法最大的挑战在于，算法采用欧几里德距离作为相似度度量，该距离度量只适用于处理类内紧密、类间分散的数据以及球形数据，不能处理非凸形状的数据。文献中很多的聚类算法均是通过改进FCM聚类算法框架中的距离度量方式，从而提升算法的性能。例如，Gustafson和Kessel等人将欧式距离度量方式改为马氏距离度量方式，提出了GK模糊聚类算法使得算法对非球形尤其是椭圆形的簇聚类效果更佳[7-8]。Yang等人利用高斯核对于离群点和噪声鲁棒的特性，结合FCM模糊聚类算法的框架，提出了AFCM聚类算法[9]。类似的例子数不胜数，这里不多做赘述。下文着重描述基于Bregman距离的模糊聚类算法，并给出了适用于FCM交替优化过程的距离函数的一般定义。

3　基于Bregman距离的模糊聚类算法

上文主要介绍了FCM算法及交替迭代优化框架。根据文中给出的交替迭代方式，可以得到目标函数的极小值。但这个结果建立在一个重要的前提下：距离的度量方式为平方欧式距离（例如二范数）或者其直接扩展得到的内积度量（例如马氏距离）等。自然地，就会有以下两个问题：（1）还有没有其他的距离度量方式适用于FCM聚类框架中，并且可以使得目标函数达到极小值；（2）这种距离的充分必要条件是什么。

针对以上问题，Xiong等人[11]将FCM算法推广到更为一般的情况。假设FCM算法框架中的距离度量方式为任意的距离函数 f(xk,vi)，可以得到基于广义距离的FCM目标函数（general-distance based fuzzy clustering algorithm,GD-FCM）[11]：

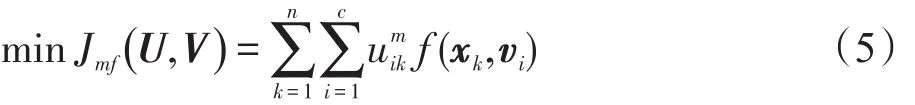
受限条件为：

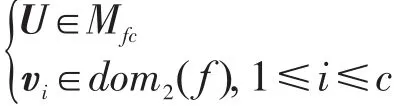
其中，f为距离函数；dom2(f)为函数 f的值域；Mfc为矩阵集合；m为模糊指数，。那么当且仅当距离 f使得目标函数单调下降时，该距离度量可以直接在FCM模糊距离框架中使用。

定理1S⊆Rd为一个非空凸集。假设连续可微函数 f:S×S↦R+满足：（1）f(x,x)=0,∀x∈S；（2）fyj(x,y)在xl上连续可微，1≤j,l≤d。如果距离 f(x,y)适用于GD-FCM，该距离度量满足 f(x,y)=φ(x)-φ(y)-(x-y)T∇φ(y)，即Bregman距离，其中φ(·)为任意凸函数。

证明 首先，证明d=1时的情形。令λk≡umik，当距离度量适用于GD-FCM时，应存在极值点：

当且仅当y*=xk时∇yf(xk,y*)=0，因此当且仅当存在唯一的λk＞0。假设存在两个不同的系数λ1,λ2＞0，那么令，有：

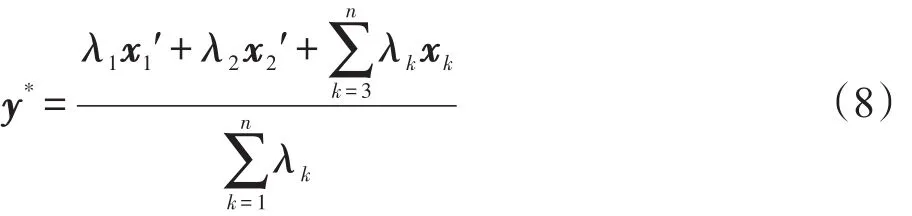
由Δ+=Δ-且∇yf在x上连续可微，对于任意k≠k′，得到。记∇y∇xf(x,y)=-h(y)，对其积分得到∇yf(x,y)=-h(y)x+I(y)。带入式（7）得到 I(y)=h(y)y。因此得到

上述只是对一维情况下的推导。若将其扩展到高维的情况，则得到距离 f(x,y)适用于GD-FCM，那么它应该满足 f(x,y)=φ(x)-φ(y)-(x-y)T∇φ(y)，其中φ(·)为任意凸函数。

与FCM算法一样，优化目标函数minJmf(U,V)得到隶属度矩阵U和聚类中心V的迭代公式（与式（3）、式（4）相同）。此时，通过迭代更新隶属度及聚类中心，可以达到目标函数的极小化。

固定聚类中心V，Jmf(U)的全局最小可以通过式（4）的隶属度迭代更新得到。在文献[12]中，Bezdek等人已证明上述命题在欧式距离条件下是成立的。同理，在给定凸函数的情况下，也可给出类似证明。

上述的分析，是在固定聚类中心或者隶属度的情况下，迭代更新公式可以取得最优解。因此，在实际中，可以通过迭代更新（即固定一个更新另一个）的方式，对目标函数进行优化。但一般算法会收敛至局部最优解，有时会收敛至鞍点。

综上所述，Bregman距离测度可以直接用于FCM聚类框架，并且通过迭代更新保证算法可以找到目标函数的局部最小值。除此之外，Bregman距离也在其他聚类算法中得到了广泛应用[13-15]。但结合FCM聚类框架与Bregman距离测度的聚类算法，即基于Bregman距离的模糊聚类算法，也存在一些的缺点，例如对噪声和异常点不鲁棒等。下文介绍的结合模糊C均值聚类框架与Total-Bregman距离的模糊聚类算法，是对基于Bregman距离的模糊聚类算法的改进。

4　Total-Bregman距离和结合FCM聚类框架与Total-Bregman距离的模糊聚类算法

4.1Total-Bregman距离

与Bregman距离不同，Total-Bregman距离通过衡量两点间的正交距离作为两点间的距离测度。Total-Bregman距离源于总体最小二乘法，与最小二乘法不同，总体最小二乘法是通过最小化正交距离的平方和寻找数据的最佳函数匹配[16]。相对于欧氏距离来说，正交距离不会随着坐标系的尺度变化或旋转而改变，稳定性优于Bregman距离。

图1给出了Total-Bregman距离和Bregman距离间差别的几何图解。其中 f(x,y)为点到线的Bregman距离，δ(x,y)为点到线的Total-Bregman距离。当坐标轴发生旋转，如图1右图所示时，Total-Bregman距离对旋转更为鲁棒。

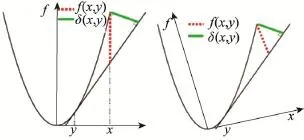
Fig.1　Total-Bregman and Bregman divergences图1　Total-Bregman距离与Bregman距离

Total-Bregman距离的定义如下：φ(·)为任意凸函数，点x与y间的Total-Bregman距离δ(x,y)等于：

与Bregman距离一样，Total-Bregman距离也可直接用于FCM算法框架（或GD-FCM算法）中。

4.2结合FCM聚类框架与Total-Bregman距离的模糊聚类算法

假设FCM算法框架中的距离度量方式为Total-Bregman距离δ(xk,vi)，那么可以得到基于Total-Bregman距离的FCM聚类算法（Total-Bregman divergence based fuzzy clustering algorithm,TBD-FCM）的目标函数如下：

受限条件为：

通过采用拉格朗日乘子法最小化目标函数，可得新的目标函数如下：

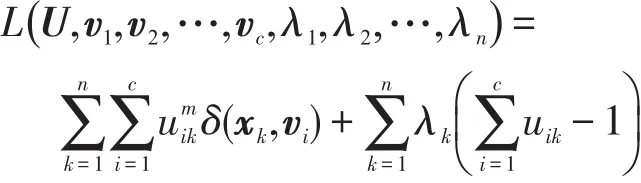
其中λ1,λ2,...,λn是拉格朗日乘子，通过求导，可得到聚类中心vk和隶属度U的迭代公式如下：

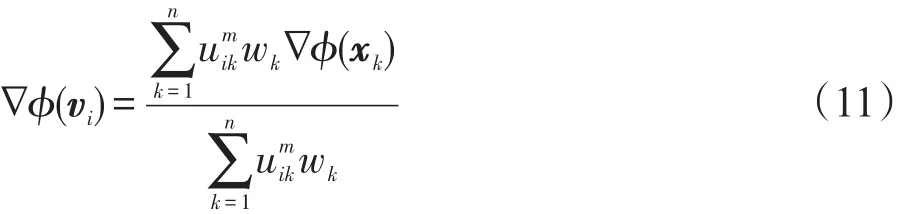
下面来证明通过式（11）、式（12）的迭代优化，可以得到目标函数的极小值。首先，给出两个定理。

定理2固定聚类中心V，Jmδ(U)的全局最小可以通过式（12）的隶属度迭代更新得到。

证明 TBD-FCM算法的隶属度迭代更新公式与FCM算法的迭代更新公式一样。但在凸函数没有给定的情况下，无法给出统一的证明。在欧氏距离条件下，该证明与FCM算法的证明类似[11-12]。□

定理3固定隶属度U，Jmδ(V)的全局最小可以通过式（11）的迭代更新公式得到。

因此，通过式（11）、式（12）的迭代优化，可以得到目标函数的极小值。换句话说，通过固定隶属度或聚类中心，其中一个更新另一个逐步减小目标函数值直至其最小值，一般算法会收敛至目标函数的局部最优解（或鞍点）。

最后，给出结合模糊C均值聚类框架与Total-Bregman距离的模糊聚类算法的实现框架。

算法2 TBD-FCM聚类算法

其中，不同的凸函数φ(·)将导致不同的聚类算法。例如当φ(x)=xTx，则得到聚类中心的迭代更新公式为v。下文将给出一些实验结果，以证明算法的有效性。

5　实验分析

本文将展示一些实验结果。实验主要围绕两个主题：（1）TBD-FCM算法的收敛性质；（2）算法的聚类结果分析。

5.1实验设置

实验数据：使用一些来自UCI数据库的实际数据。UCI数据库是加州大学欧文分校（University of California Irvine）提出的用于机器学习的数据库，这个数据库是一个常用的标准测试数据集。表1列出了实验中使用的数据集。其中“CV”表示数据集的变异系数，该系数表示数据的类不平衡度。

实验工具：用Matlab作为实验平台。首先，对随机初始化隶属度矩阵、随机初始化聚类中心和用户指定聚类中心这3种初始化方式进行筛选，最终决定随机初始化隶属度矩阵，而后通过迭代更新对隶属度和聚类中心进行求解。其次，对于算法的迭代停止条件，采用Bezdek提出的迭代停止条件[17]，当时，迭代停止。其中ε为迭代停止阈值，一般设为10-5或10-6。本文用Matlab R2010a作为编程环境实现算法。

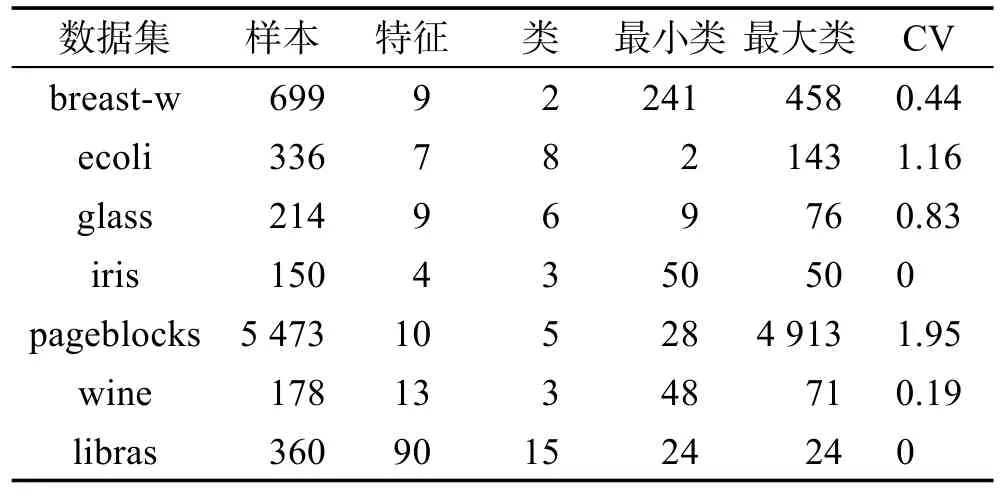
Table 1　Data sets used in experiment表1　实验中使用数据集

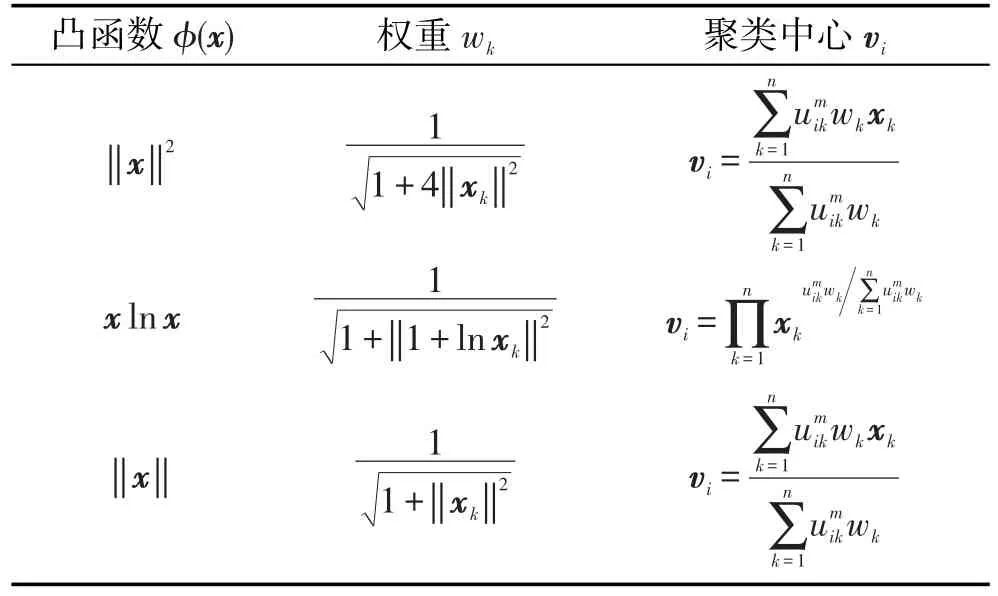
Table 2　Distance measure used in experiment表2　实验中使用距离度量

聚类结果度量：使用来自UCI数据库的一些实际数据集，因此这些数据是有类标的。目前通过一个普遍适用的NVI指数（normalized variation of information）可以衡量聚类结果的准确率[18]。假设包含n个数据的数据集X本身包含c′个类，实验中指定分类个数为c。根据得到的划分矩阵U*，求解求和矩阵Z*：

其中，Cj′表示实际的第j类。令，NVI指数定义为：

5.2收敛性质的分析

第4章从理论角度分析了TBD-FCM算法的收敛性质。从结论中可以看出，在FCM聚类框架中使用Total-Bregman距离可以保证算法收敛到局部最优值。本节通过实验验证TBD-FCM算法的收敛性。采用来自UCI数据库的数据集（如表1所示）进行验证。实验中主要验证凸函数为||x||2、xlnx和||x||时的TBD-FCM算法的收敛性。为了减少随机初始化聚类中心带来的影响，实验中对于每个凸函数每个数据集聚类10次，选择最优的聚类结果。实验最大迭代次数为50，模糊指数m=2。

表3显示了目标函数随着迭代次数变化的趋势。表中用不同颜色的曲线表示使用不同凸函数时TBD-FCM算法的目标函数。例如，凸函数为||x||2时使用蓝色线条，而凸函数为xlnx时使用红色线条。

从表3中可以看出，TBD-FCM算法的目标函数在这些数据集上均表现出单调下降的趋势。实验中，对每个数据集每种凸函数均聚类10次，每次结果中，目标函数都呈单调递减趋势。这也表示，TBD-FCM算法对于大多数的数据而言，具有较好的收敛性。

5.3TBD-FCM算法的聚类结果分析

上节从实验角度证明了TBD-FCM算法具有收敛性，可以通过迭代更新收敛到局部最优点。但在实际的聚类过程中，人们更为关心算法的聚类结果。

下面对TBD-FCM算法的聚类结果进行分析。仍然采用表3中的数据集进行聚类分析。然后用式（14）给出的NVI指数对聚类结果进行评价，NVI越大表明聚类结果越差。结果在表4中展示。通过对比基于Bregman距离的模糊聚类算法以及结合模糊C均值聚类框架与Total-Bregman距离的模糊聚类算法的聚类结果可以看出，通过将Bregman距离改为Total-Bregman距离，可以提升聚类的精确度。在大多数情况下，使用同样的凸函数对同样的数据集进行聚类，TBD-FCM算法聚类结果的NVI值比GD-FCM算法聚类结果的NVI值小，说明使用Total-Bregman距离比使用Bregman距离有更好的聚类效果。

Table 3　Convergence properties of TBD-FCM algorithm表3　TBD-FCM算法收敛性质分析

Table 4　Clustering result of TBD-FCM algorithm and GD-FCM algorithm表4　TBD-FCM算法和GD-FCM算法聚类结果分析

6　结束语

聚类算法在很多科学领域均得到了非常广泛的应用，同时，怎样提升聚类结果的精确度，也成为机器学习研究的热点。近年来，专家学者们对原有的聚类算法进行改进或提出新的聚类算法，为更好地对数据进行聚类做出了显著的贡献。本文旨在介绍结合模糊C均值聚类框架与Total-Bregman距离的模糊聚类算法，分析其优劣性质，并从理论和实验角度证明算法的收敛性，为更好地应用该聚类算法提供参考。并且通过实验验证了提出的TBD-FCM算法较GD-FCM算法有更好的聚类效果。当然，本文没有对所有的结合模糊C均值聚类框架与Total-Bregman距离的模糊聚类算法进行分析，只对其中一部分的算法进行了分析和实验验证，以后会继续研究结合模糊C均值聚类框架与Total-Bregman距离的模糊聚类算法，对更多的距离度量下的算法性能进行分析。

References:

[1]Bai Xue,Luo Siwei,Huang Yaping.Similarity measures in cluster analysis and its applications[D].Beijing:Beijing Jiaotong University,2012.

[2]Everitt B S.Cluster analysis[M].London:Halstead Press, 1974.

[3]Zhang Li,Zhou Weida,Jiao Licheng.Kernel clustering algorithm[J].Chinese Journal of Computers,2002,25(6):587-590.

[4]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8 (3):338-353.

[5]Dunn J C.A fuzzy relative of the ISODATA process and its use in detecting compact well separated clusters[J].Journal of Cybernetics,1974,3(3):32-57.

[6]Lu Qiugen.The research and realization of fuzzy clustering algorithm[J].Computer Knowledge and Technology,2008, 3(9):1987-1990.

[7]Gustafson D E,Kessel W C.Fuzzy clustering with a fuzzy covariance matrix[C]//Proceedings of the 1978 IEEE Conference on Decision and Control,San Diego,USA,Jan 10-12,1979.Piscataway,USA:IEEE,1979:761-766.

[8]Krishnapuram R,Kim J.A note on the Gustafson-Kessel and adaptive fuzzy clustering algorithms[J].IEEE Transactions on Fuzzy Systems,1999,7(4):453-461.

[9]Wu K L,Yang M S.Alternative C-means clustering algorithms[J].Pattern recognition,2002,35(10):2267-2278.

[10]Yang M S,Wu K L,Yu J.Anovel fuzzy clustering algorithm [C]//Proceedings of the 2003 IEEE International Symposium on Computational Intelligence in Robotics and Automation.Piscataway,USA:IEEE,2003,2:647-652.

[11]Wu Junjie,Xiong Hui,Liu Chen,et al.A generalization of distance functions for fuzzy C-means clustering with centroids of arithmetic means[J].IEEE Transactions on Fuzzy Systems,2012,20(3):557-571.

[12]Hathaway R,Bezdek J,Tucker W.An improved convergence theory for the fuzzy C-means clustering algorithms[J]. Analysis of Fuzzy Information,1987,3:123-131.

[13]Shen Guowei,Yang Wu,Wang Wei,et al.Agglomerative hier-archical co-clustering based on bregman divergence[M]// Recent Advances on Soft Computing and Data Mining.Berlin:Springer International Publishing,2014:389-398.

[14]Nielsen F,Nock R.Optimal interval clustering:application to Bregman clustering and statistical mixture learning[J]. arXiv:1403.2485,2014.

[15]Iyer R,Bilmes J A.The Lovász-Bregman divergence and connections to rank aggregation,clustering,and Web ranking[J]. arXiv:1408.2062,2014.

[16]Groen P D.An introduction to total least squares[J].Nieuw Archief voor Wiskunde,1996,14(4):237-253.

[17]Bezdek J C.Pattern recognition with fuzzy objective function algorithms[M].[S.l.]:Springer US,1981. [18]Wu Junjie,Xiong Hui,Chen Jian.Adapting the right measures for k-means clustering[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Paris,France,Jun 28-Jul 1, 2009.New York,USA:ACM,2009:877-886.

附中文参考文献：

[1]白雪,罗四维,黄雅平.聚类分析中的相似性度量及其应用研究[D].北京:北京交通大学,2012.

[3]张莉,周伟达,焦李成.核聚类算法[J].计算机学报,2002, 25(6):587-590.

[6]卢秋根.模糊聚类算法的研究与实现[J].电脑知识与技术,2008,3(9):1987-1990.

Chaomurilige was born in 1988.She is a Ph.D.candidate at School of Computer and Information Technology,Beijing Jiaotong University.Her research interests include machine learning and clustering analysis,etc.

超木日力格（1988—），女，内蒙古通辽人，北京交通大学计算机与信息技术学院博士研究生，主要研究领域为机器学习，聚类分析等。

于剑（1969—），男，山东人，2000年于北京大学应用数学专业获得博士学位，现为北京交通大学计算机与信息技术学院教授、博士生导师，交通数据分析与挖掘北京市重点实验主任，CCF高级会员，主要研究领域为机器学习，图像处理，模式识别等。

ZHU Jie was born in 1982.He is a Ph.D.candidate at School of Computer and Information Technology,Beijing Jiaotong University.His research interests include machine learning and computer vision,etc.

朱杰（1982—），男，河北保定人，北京交通大学计算机与信息技术学院博士研究生，主要研究领域为机器学习，机器视觉等。

Fuzzy ClusteringAlgorithm Based on Total-Bregman Divergence*

Chaomurilige1,YU Jian1+,ZHU Jie1,2
1.Beijing Key Lab of Traffic Data Analysis and Mining,School of Computer and Information Technology,Beijing Jiaotong University,Beijing 100044,China
2.Department of Information Management,The Central Institute for Correctional Police,Baoding,Hebei 071000,China
+Corresponding author:E-mail:jianyu@bjtu.edu.cn

The fuzzy C-means(FCM)clustering algorithm is one of the widely used clustering algorithms based on the minimization of objective function.Several clustering algorithms,such as AFCM algorithm and GK algorithm, are the extension and improvement of FCM clustering algorithm.This paper introduces Total-Bregman divergence into the FCM clustering framework and proposes an algorithm named fuzzy clustering algorithm based on total-Bregman divergence(TBD-FCM),which is an improvement of the fuzzy clustering algorithm based on Bregman divergence.Then this paper analyzes the convergence properties of this algorithm.In experiment part,several clustering results on the datasets from the UCI repository have been shown to prove the effectiveness and the convergence properties of clustering algorithm.

clustering algorithm;fuzzy clustering;Total-Bregman divergence

2015-05,Accepted 2015-08.

YU Jian was born in 1969.He the Ph.D.degree in applied mathematics from Peking University in 2000. Now he is a professor and Ph.D.supervisor at Beijing Jiaotong University,the director of the Beijing Key Lab of Traffic Data Analysis and Mining,and the senior member of CCF.His research interests include machine learning, image processing and pattern recognition,etc.

10.3778/j.issn.1673-9418.1505054

*The National Natural Science Foundation of China under Grant No.61370129(国家自然科学基金);the Specialized Research Fund for the Doctoral Program of Higher Education of China under Grant No.20120009110006(高等学校博士学科点专项科研基金).

CNKI网络优先出版：2015-08-12,http://www.cnki.net/kcms/detail/11.5602.tp.20150812.1636.007.html

A

TP301