密度峰值优化初始中心的K-medoids聚类算法*
谢娟英,屈亚楠
陕西师范大学 计算机科学学院,西安 710062
密度峰值优化初始中心的K-medoids聚类算法*
谢娟英+,屈亚楠
陕西师范大学 计算机科学学院,西安 710062
针对快速K-medoids聚类算法和方差优化初始中心的K-medoids聚类算法存在需要人为给定类簇数,初始聚类中心可能位于同一类簇,或无法完全确定数据集初始类簇中心等缺陷,受密度峰值聚类算法启发,提出了两种自适应确定类簇数的K-medoids算法。算法采用样本xi的t最近邻距离之和倒数度量其局部密度ρi,并定义样本xi的新距离δi,构造样本距离相对于样本密度的决策图。局部密度较高且相距较远的样本位于决策图的右上角区域,且远离数据集的大部分样本。选择这些样本作为初始聚类中心,使得初始聚类中心位于不同类簇,并自动得到数据集类簇数。为进一步优化聚类结果,提出采用类内距离与类间距离之比作为聚类准则函数。在UCI数据集和人工模拟数据集上进行了实验测试,并对初始聚类中心、迭代次数、聚类时间、Rand指数、Jaccard系数、Adjusted Rand index和聚类准确率等经典聚类有效性评价指标进行了比较,结果表明提出的K-medoids算法能有效识别数据集的真实类簇数和合理初始类簇中心,减少聚类迭代次数,缩短聚类时间,提高聚类准确率,并对噪音数据具有很好的鲁棒性。
聚类;K-medoids算法;初始聚类中心;密度峰值;准则函数
1 引言
聚类基于“物以类聚”原理将一组样本按照相似性归成若干类簇,使得属于同一类簇的样本之间差别尽可能小,而不同类簇的样本间差别尽可能大。聚类算法包括基于划分的方法、基于层次的方法、基于密度的方法、基于网格的方法和基于模型的方法[1]。经典的划分式聚类算法包括K-means算法[2]和K-medoids算法[3]。K-medoids算法克服了K-means算法对孤立点敏感的缺陷,PAM(partitioningaroundmedoids)算法[3-4]是最经典的K-medoids算法。然而,K-medoids算法同K-means算法一样,存在着聚类结果随初始聚类中心改变而变化的问题。
快速K-medoids算法[5]从初始聚类中心选择和聚类中心更迭两方面对PAM算法进行改进,取得了远优于PAM算法的聚类效果。然而快速K-medoids算法选择的初始聚类中心可能位于同一类簇。邻域K-medoids聚类算法[6]提出邻域概念,使选择的初始聚类中心尽可能位于不同样本分布密集区,得到了优于快速K-medoids算法的聚类效果,但该算法的邻域半径需要人为设定。引入粒度概念,定义粒子密度,选择密度较大的前K个粒子的中心样本作为K-medoids算法的初始聚类中心,得到了更好的初始聚类中心和聚类结果,且避免了文献[6]主观选择邻域半径的缺陷[7-8]。但是基于粒计算的K-medoids算法[7]构造样本去模糊相似矩阵时需要人为给定阈值。粒计算优化初始聚类中心的K-medoids算法将粒计算与最大最小距离法结合[9],且使用所有样本的相似度均值作为其构造去模糊相似度矩阵的阈值,改进了文献[7]需要人为设定阈值进行模糊相似矩阵去模糊操作的缺陷。文献[10]中算法完全依赖数据集自身的分布信息,以方差作为样本分布密集程度度量,分别以样本间距离均值和相应样本标准差为邻域半径,选取方差值最小且其间距离不低于邻域半径的样本为初始聚类中心,使K-medoids算法的初始聚类中心尽可能完全反应数据集样本原始分布信息,得到优于快速K-medoids和邻域K-medoids算法的聚类结果,且不需要任何主观参数选择。但是该算法当邻域半径过大时,不能得到数据集真实类簇数。Rodriguez等人[11]基于聚类中心比其近邻样本密度高且与其他密度较高样本的距离相对较远的特点,提出快速搜索密度峰值聚类算法(clustering by fast search and find of density peaks,DPC),以密度峰值点样本为类簇中心,自动确定类簇个数,并分配样本到距离最近的密度较高样本所在类簇实现聚类。但是该算法需要人为给定截断距离参数,聚类结果随截断距离参数改变而波动。
本文针对快速K-medoids算法[5]和方差优化初始中心K-medoids算法[10]的潜在缺陷,受文献[11]启发,提出了密度峰值优化初始中心的K-medoids聚类算法DP_K-medoids(density peak optimized K-medoids)。DP_K-medoids算法使用样本xi的t近邻距离之和的倒数度量样本xi的局部密度ρi,并定义样本xi的距离δi为样本xi到密度大于它的最近样本xj的距离的指数函数,构造样本距离相对于样本密度的决策图,选择决策图中样本密度ρ和样本距离δ都较高,且明显远离数据集大部分样本点的决策图右上角的密度峰值点作为初始聚类中心,使得初始聚类中心位于不同类簇,同时自适应地确定类簇个数。
划分式聚类算法的思想是使类内距离尽可能小,而类间距离尽可能大,因此本文提出以类内距离与类间距离之比作为新聚类准则函数,得到了改进DP_K-medoids算法DPNM_K-medoids(density peak optimized K-medoids with new measure)。其中类内距离度量定义为聚类误差平方和,类间距离定义为各类簇中心样本距离之和。
通过UCI数据集和人工模拟数据集实验测试,以及对不同聚类有效性指标进行比较,结果表明本文提出的DP_K-medoids算法和DPNM_K-medoids算法均能识别数据集的类簇数,并选择到数据集的合理初始聚类中心,有效减少了聚类迭代次数,缩短了聚类时间,提高了聚类准确率。
2 基本概念
设给定含n个样本的数据集X={x1,x2,…,xn},每个样本有p维特征,欲将其划分为k个类簇Cj,j= 1,2,…,k,k<n,第i个样本的第 j个属性值为xij。


3 本文K-medoids算法
本文提出密度峰值优化初始中心的K-medoids聚类算法,主要针对快速K-medoids算法和方差优化初始中心的K-medoids算法的缺陷展开,其主要贡献是样本xi的局部密度ρi采用其t最近邻距离之和的倒数度量,样本xi的距离δi定义为样本xi到密度大于它的最近样本xj的距离的指数函数,利用样本距离相对于样本密度的决策图,自适应地确定数据集类簇数和K-medoids算法的合理初始类簇中心。
3.1DP_K-medoids算法思想
针对快速K-medoids算法和方差优化初始中心K-medoids算法需要人为设定类簇数k,以及前者初始聚类中心可能位于同一类簇,后者初始聚类中心受到邻域半径影响,可能不能得到数据集真实类簇数的缺陷,本文DP_K-medoids算法使用样本的t最近邻距离之和的倒数度量样本xi的局部密度ρi,采用式(6)定义度量样本xi的距离δi。以ρ为横轴,δ为纵轴构造样本距离相对于样本密度的决策图,选择决策图中样本密度ρ和样本距离δ都较高,且明显远离大部分样本点的决策图右上角区域的密度峰值点为初始类簇中心,密度峰值点个数即为类簇数,使选择的初始聚类中心位于不同类簇。
步骤1初始化。
(1)根据式(7)对样本进行标准化;
(2)根据式(5)计算样本xi的局部密度ρi,根据式(6)计算样本xi的距离δi;
(3)构造以ρ为横轴,δ为纵轴的决策图,选择决策图中样本密度ρ和样本距离δ都较高,且明显远离大部分样本的右上角区域的密度峰值点为初始聚类中心,密度峰值点个数为类簇数k。
步骤2构造初始类簇。
(1)根据距离最近原则,将其余样本点分配到最近初始类簇中心,形成初始划分;
(2)计算聚类误差平方和。
步骤3更新类簇中心并重新分配样本。
(1)为每个类簇找一个新中心,使得簇内其余样本到新中心距离之和最小,用新中心替换原中心;
(2)重新分配每个样本到最近类簇中心,获得新聚类结果,计算聚类误差平方和;
(3)若当前聚类误差平方和与前次迭代聚类误差平方和相同,则算法停止,否则转步骤3。
3.2DPNM_K-medoids算法思想
DPNM_K-medoids使用类内距离与类间距离之比作为聚类准则函数,求聚类表达式(4)的最小优化。当准则函数达到最小值时,得到最优聚类结果。DPNM_K-medoids算法的初始聚类中心选择与DP_K-medoids的初始聚类中心选择方法相同,二者的区别在于聚类准则函数不同,也就是聚类的停止条件不同。将DP_K-medoids算法的步骤2和步骤3计算聚类误差平方和修改为计算聚类结果的新聚类准则函数值,同时将步骤3中的第3小步修改为,若当前新聚类准则函数值不小于前次迭代的新聚类准则函数值,则算法停止,否则转步骤3继续执行,便得到DPNM_K-medoids算法。
3.3本文K-medoids算法分析
K-medoids算法的时间复杂度由初始聚类中心选择和聚类中心更迭两部分组成。密度峰值聚类算法的时间复杂度由初始聚类中心选择和样本分配两部分组成。
本文DP_K-medoids和DPNM_K-medoids算法,以及密度峰值聚类算法[11]通过计算样本局部密度和样本距离选取初始聚类中心。由式(5)样本局部密度计算和式(6)样本距离计算以及密度峰值聚类算法描述[11]可见,该3种算法计算一个样本局部密度与距离的时间复杂度均为Ο(n),因此本文DP_K-medoids和DPNM_K-medoids算法,以及密度峰值聚类算法[11]计算所有样本密度的时间复杂度为Ο(n2)。
快速K-medoids算法[5]通过计算样本全局密度选取初始聚类中心。方差优化初始中心的MD_K-medoids和SD_K-medoids算法[10]通过计算样本方差选取初始聚类中心。快速K-medoids算法[5]和方差优化初始中心的K-medoids算法[10]计算一个样本密度的时间复杂度分别为Ο(n2)和Ο(n),因此快速K-medoids算法计算所有样本密度的时间复杂度为Ο(n3),方差优化初始中心的K-medoids算法计算所有样本方差的时间复杂度为Ο(n2)。
本文两种K-medoids算法、快速K-medoids算法[5]、方差优化初始中心的MD_K-medoids和SD_K-medoids算法[10]聚类中心更迭的时间复杂度均为Ο(nk×iter),其中iter为算法迭代次数,n为样本数,k为类簇数。密度峰值聚类算法[11]在获得初始聚类中心后,将其余样本分配给密度比它大的最近邻样本所在类簇,因此样本分配时间复杂度为Ο(n)。
因此,本文DP_K-medoids和DPNM_K-medoids算法,以及方差优化初始中心的MD_K-medoids和SD_K-medoids算法的时间复杂度为Ο(n2+nk×iter)。快速K-medoids算法的时间复杂度为Ο(n3+nk× iter)。密度峰值聚类算法的时间复杂度为Ο(n2+n)。由此可见,尽管上述6种聚类算法的时间复杂度可统一表达为O(n2)数量级,但密度峰值聚类算法是该6种聚类算法中速度最快的聚类算法。
5种K-medoids算法均先获得k个初始聚类中心,然后根据距离最近原则将其余样本分配到最近初始聚类中心,得到初始类簇划分。初始划分通常不是最优聚类结果,当前聚类准则函数值通常不是最小的。此时,进行聚类中心更迭,当一次聚类中心更替发生,并重新分配样本得到新类簇分布时,计算当前分布的聚类准则函数值,若比上次迭代的聚类准则函数值小,则继续迭代。经过若干次迭代后,聚类准则函数值达到最小,即聚类结果不再发生改变,聚类算法收敛到最优解。
4 实验结果与分析
为了测试本文K-medoids算法的性能,分别在UCI数据集和两种人工模拟数据集上进行实验。实验环境是Inter®CoreTMi5-3230M CPU@2.60 GHz,4GB内存,400GB硬盘,Matlab应用软件。
算法聚类结果采用迭代次数、聚类时间、聚类准确率,以及外部有效性评价指标Rand指数[12]、Jaccard系数[13-15]和Adjusted Rand index[16-17]参数进行评价。
4.1UCI数据集实验结果与分析
本部分实验采用UCI机器学习数据库[18]的iris等13个聚类算法常用数据集对本文算法进行测试。所用数据集描述见表1,pid是pima indians diabetes数据集的简写,waveform40是waveform21增加19个噪音属性得到的数据集。本文DP_K-medoids和DPNM_ K-medoids算法分别与快速K-medoids算法[5]、方差优化初始中心的MD_K-medoids和SD_K-medoids算法[10],以及密度峰值聚类算法[11]进行比较,以检验本文提出的密度峰值优化初始中心的K-medoids算法的有效性。
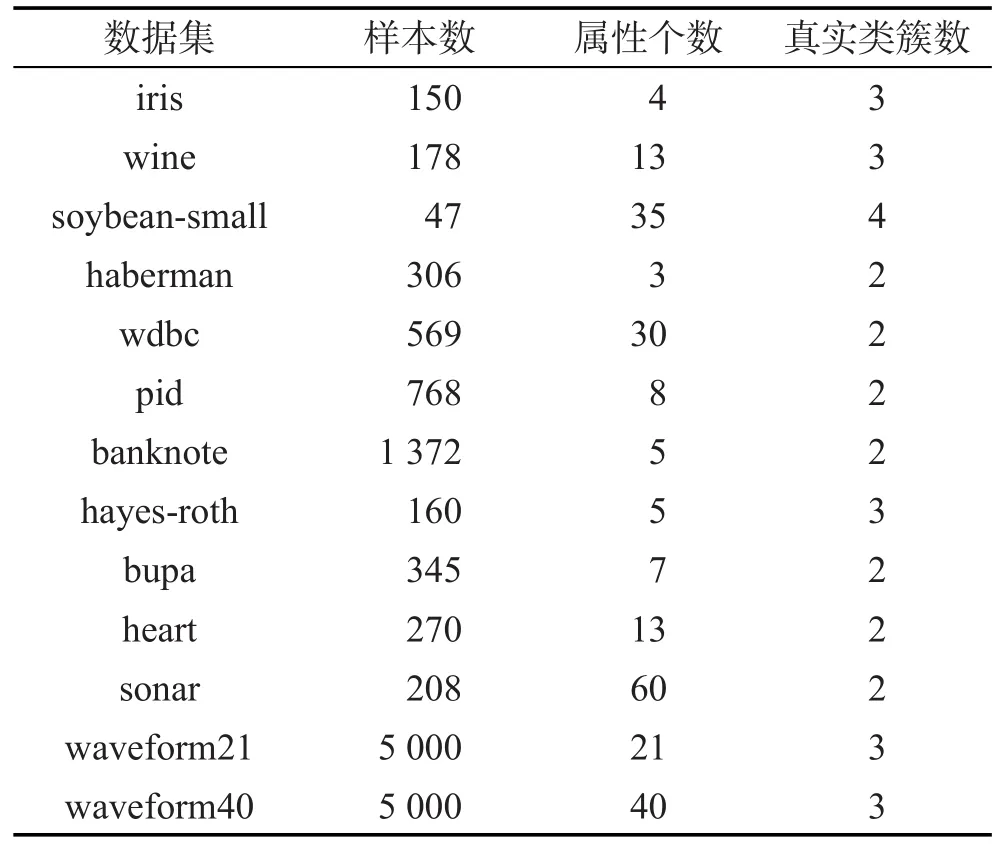
Table 1 Datasets from UCI machine learning repository表1 UCI数据集描述
由于各数据集样本空间分布不同,本文K-medoids算法选取的样本最近邻数t值也不尽相同,数据集haberman、hayes-roth、sonar、waveform21和 waveform40的样本最近邻数t=6,数据集pid的样本最近邻数t=7,其余7个UCI数据集的样本最近邻数t=8。密度峰值聚类算法的结果随截断距离参数值的改变而不同,实验展示的是在各数据集多次实验得到的最好聚类结果值。本文K-medoids算法在UCI数据集上的决策图及其初始聚类中心如图1所示,图中矩形框内的加粗黑圆点为所选初始聚类中心。表2是6种聚类算法对表1 UCI数据集选择的初始聚类中心样本。表3是6种聚类算法对表1 UCI数据集10次运行的平均迭代次数和平均聚类时间。其中,加粗字体表示相应的最好实验结果。密度峰值聚类算法不存在聚类中心更迭的过程,因而比较算法平均迭代次数时不将密度峰值聚类算法作为对比算法。图2展示了6种聚类算法的Rand指数、Jaccard系数、AdjustedRandindex参数和聚类准确率的平均值比较。
图1所示实验结果对比表1的数据集描述可以看出,本文两种K-medoids算法能发现数据集的真实类簇数和相应的初始聚类中心。因此,本文两种K-medoids算法克服了快速K-medoids算法、MD_K-medoids算法和SD_K-medoids算法需要人为给定类簇数,及其选择初始类簇中心时的缺陷。

Fig.1 Decision graphs and initial seeds of the proposed K-medoids algorithms on UCI datasets图1 本文K-medoids算法对各UCI数据集的决策图及其初始聚类中心
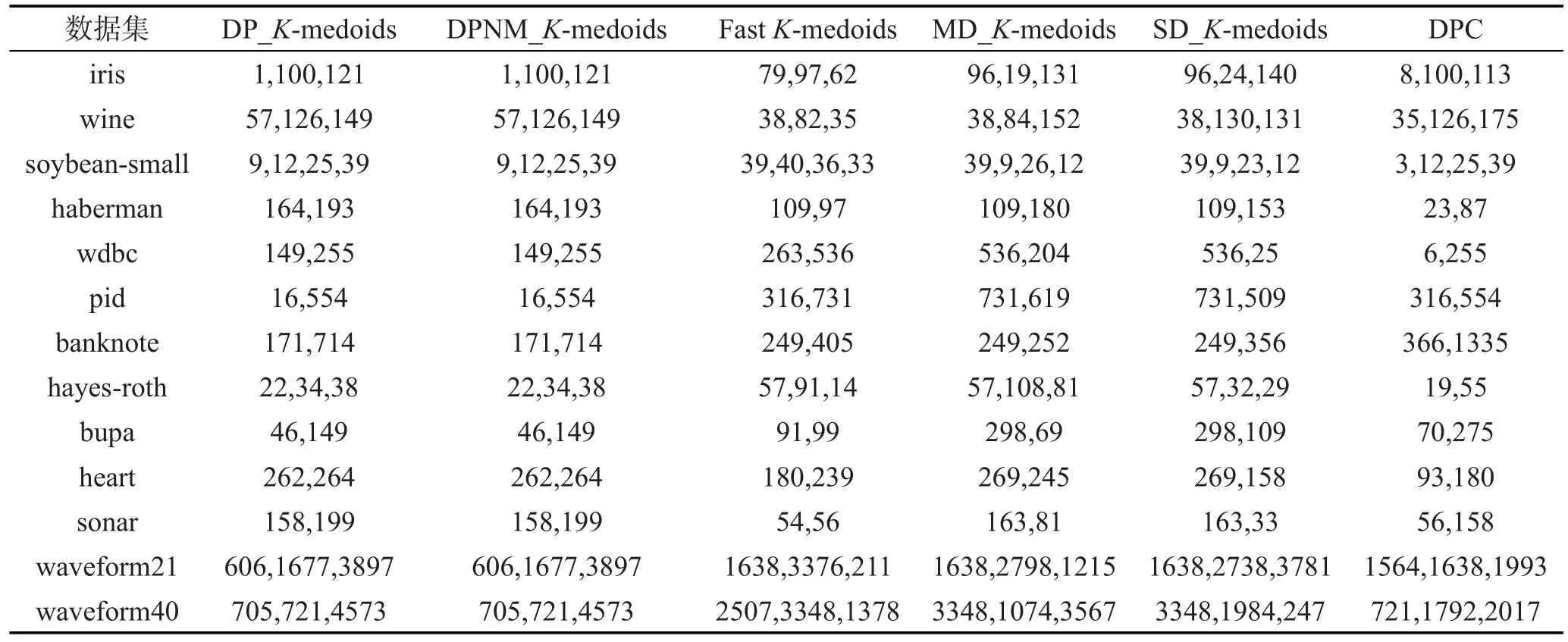
Table 2 Initial seeds selected by six algorithms on UCI datasets表2 6种算法在UCI数据集上选择的初始聚类中心
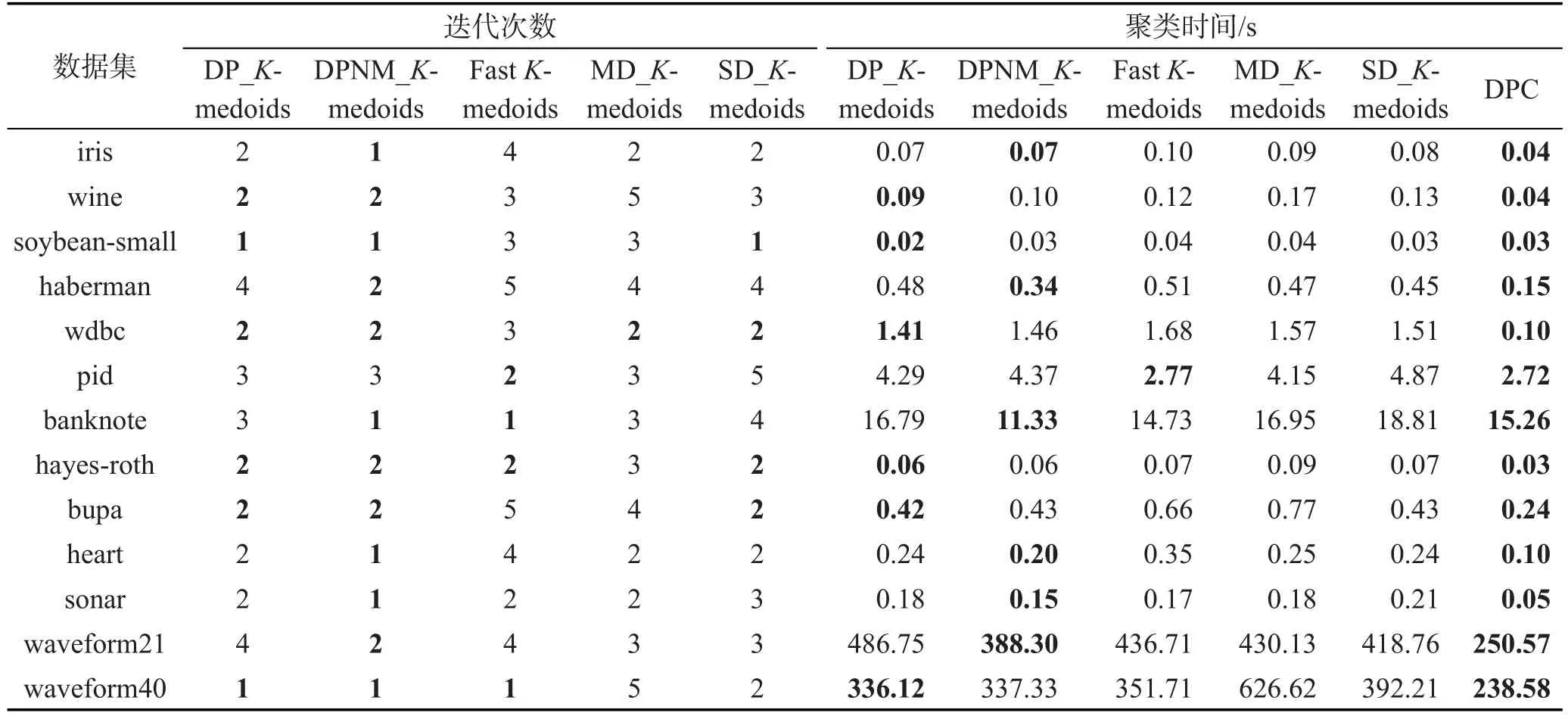
Table 3 Iterations and clustering time of six algorithms on UCI datasets表3 UCI数据集上6种算法的迭代次数和聚类时间
分析表2实验结果与各数据集真实分布可知,本文DP_K-medoids和DPNM_K-medoids算法除了在haberman、banknote、hayes-roth和sonar数据集选择的初始聚类中心存在位于同一类簇的现象,在其余9个UCI数据集上选择的初始聚类中心均位于不同类簇。快速K-medoids算法在iris、wine、pid和bupa这4个数据集选择的初始聚类中心位于不同类簇,在其余9个数据集的初始聚类中心均存在位于同一类簇的现象。MD_K-medoids算法在7个数据集选择的初始聚类中心位于不同类簇,在haberman、pid、banknote、hayes-roth、bupa和heart数据集选择的初始聚类中心位于同一类簇。SD_K-medoids算法在haberman、banknote、hayes-roth、heart和waveform21数据集选择的初始聚类中心位于同一类簇,在其余8个数据集选择的初始聚类中心均位于不同类簇。密度峰值聚类算法在7个数据集选择的初始聚类中心位于不同类簇,在haberman、pid、hayes-roth、bupa、waveform21和waveform40数据集选择的初始聚类中心均存在位于同一类簇的现象。由此可见,本文提出的DP_K-medoids和DPNM_K-medoids算法选择的初始聚类中心更好,从而可以得到较好的初始类簇划分,加快算法收敛速度,并增加算法收敛到全局最优解的概率。
从表3所示实验结果可以看出,本文提出的两种K-medoids算法在除数据集pid之外的其他12个UCI数据集上的迭代次数和运行时间都优于其他3种K-medoids算法。快速K-medoids算法在pid数据集的迭代次数和聚类时间都最优。表3实验结果揭示,本文DPNM_K-medoids算法的迭代次数优于DP_K-medoids算法,在迭代次数相同的情况下,本文DP_K-medoids算法的运行时间更快。分析原因是,本文DPNM_K-medoids算法采用新聚类准则作为收敛性判断依据,而DP_K-medoids算法采用聚类误差平方和作为聚类准则判断算法是否收敛。新聚类准则函数值需要更多计算时间,因此当迭代次数相同时,DP_K-medoids算法的运行时间更快。密度峰值聚类算法在13个UCI数据集上的聚类时间是6种聚类算法中最短的,与3.3节的算法分析结果一致。密度峰值聚类算法聚类时间最短的原因是:密度峰值聚类算法的样本分配策略是一步分配,使其时间消耗最少。

Fig.2 Rand index,Jaccard coefficient,Adjusted Rand index and clustering accuracy of six algorithms on UCI datasets图2 6种算法在UCI数据集上的Rand指数、Jaccard系数、Adjusted Rand index参数和聚类准确率
从图2可以看出,本文DP_K-medoids和DPNM_K-medoids聚类算法在soybean-small数据集的4个聚类有效性指标Rand指数、Jaccard系数、Adjusted Rand index参数和聚类准确率均不如方差优化初始聚类中心的K-medoids算法和密度峰值聚类算法,但是优于快速K-medoids算法。图2显示,密度峰值聚类算法在banknote数据集的4个聚类有效性指标均值高于其余5种K-medoids算法,原因是,5种K-medoids算法对该数据集初始聚类中心确定后,均根据距离最近原则,将数据划分为上下分布的两个类簇;而密度峰值聚类算法根据密度较大最近邻样本所在类簇将数据划分为左右分布的两个类簇,符合banknote数据集的真实类簇分布。从图2还可以看出,密度峰值聚类算法在数据集haberman的Rand指数、Jaccard系数和聚类准确率高于其余5种K-medoids算法,Adjusted Rand index稍低于其余算法。图2还显示,SD_K-medoids在waveform40数据集的4个聚类有效性指标均优于其余算法,而密度峰值聚类算法在该数据集的各项指标值最差。从图2(a)可见,本文提出的两种K-medoids算法在其他10个数据集的聚类有效性指标都优于其他3种K-medoids算法。图2(b)显示,本文K-medoids算法在8个UCI数据集的聚类有效性指标Jaccard系数值优于其他3种K-medoids算法;快速K-medoids算法在banknote数据集的聚类有效性指标Jaccard系数最好,方差优化初始聚类中心的MD_K-medoids算法在hayes-roth和bupa数据集的Jaccard系数聚类指标最优。图2(c)关于各算法聚类结果的Adjusted Rand index参数比较揭示,本文算法在10/13个数据集的聚类性能最好,方差优化初始聚类中心的MD_K-medoids算法在hayes-roth数据集的聚类效果最好。图2(d)的聚类准确率比较揭示,本文算法在8/13个数据集的聚类准确率高于其他3种K-medoids算法,快速K-medoids算法在hayes-roth数据集聚类准确率最高,方差优化初始聚类中心的K-medoids算法在bupa和soybean-small数据集聚类准确率最高。
综合以上分析可知,本文提出的DP_K-medoids和DPNM_K-medoids算法能在较短时间内实现对数据集的有效聚类,各项聚类有效性指标比较揭示本文两种K-medoids算法整体性能更优。
4.2人工数据集实验结果与分析
本实验分为两部分,分别测试本文提出的两种K-medoids算法的鲁棒性,以及其对经典人工数据集的聚类性能。
4.2.1本文K-medoids算法鲁棒性测试实验
为测试本文算法的鲁棒性,随机生成分别含有0%、5%、10%、15%、20%、25%、30%、35%、40%、45%不同比例噪音的人工模拟数据集。每一组数据集含有4个类簇,每一类簇有100个二维样本,这些样本符合正态分布。其中第i类簇的均值为 μi,协方差矩阵为σi,在第一类簇加入噪音数据,噪音数据的协方差矩阵为σn,数据集的生成参数如表4所示。第一类簇分布在数据集的中间,在中间类簇加入噪音数据,使其与周围3个类簇的样本都有部分交叠,以更好地测试本文算法的鲁棒性。

Table 4 Parameters to generate synthetic datasets表4 人工模拟数据集的生成参数
在10组含有不同比例噪音的人工模拟数据集上分别运行本文DP_K-medoids和DPNM_K-medoids算法、快速K-medoids算法、MD_K-medoids算法和SD_K-medoids算法以及密度峰值聚类算法。每个算法各运行10次,实验结果为10次运行的平均值。表5为6种算法在各数据集选择的初始聚类中心,表6为6种算法的迭代次数和聚类时间,图3为6种算法对各数据集聚类结果的Rand指数、Jaccard系数、Adjusted Rand index参数和聚类准确率比较。
从表5中可以看出,本文算法对该10组含噪人工模拟数据集确定的类簇数与数据集真实类簇数一致,且针对各数据集选择的初始聚类中心分布在不同类簇。对该10组含不同比例噪音的人工模拟数据集,MD_K-medoids算法选择的初始聚类中心均位于不同类簇,快速K-medoids算法选择的初始聚类中心存在位于同一类簇的现象,SD_K-medoids算法在噪音比例为20%和25%的人工模拟数据集上选择的初始聚类中心存在两个中心位于同一类簇的现象,密度峰值聚类算法在噪音比例为30%时存在两个类簇中心位于同一类簇的现象。因此,快速K-medoids算法在该10组含噪音人工模拟数据集上选择的初始聚类中心是5种K-medoids算法中最差的,本文K-medoids算法选择的初始聚类中心最优,MD_K-medoids算法和SD_K-medoids算法以及密度峰值聚类算法居中。
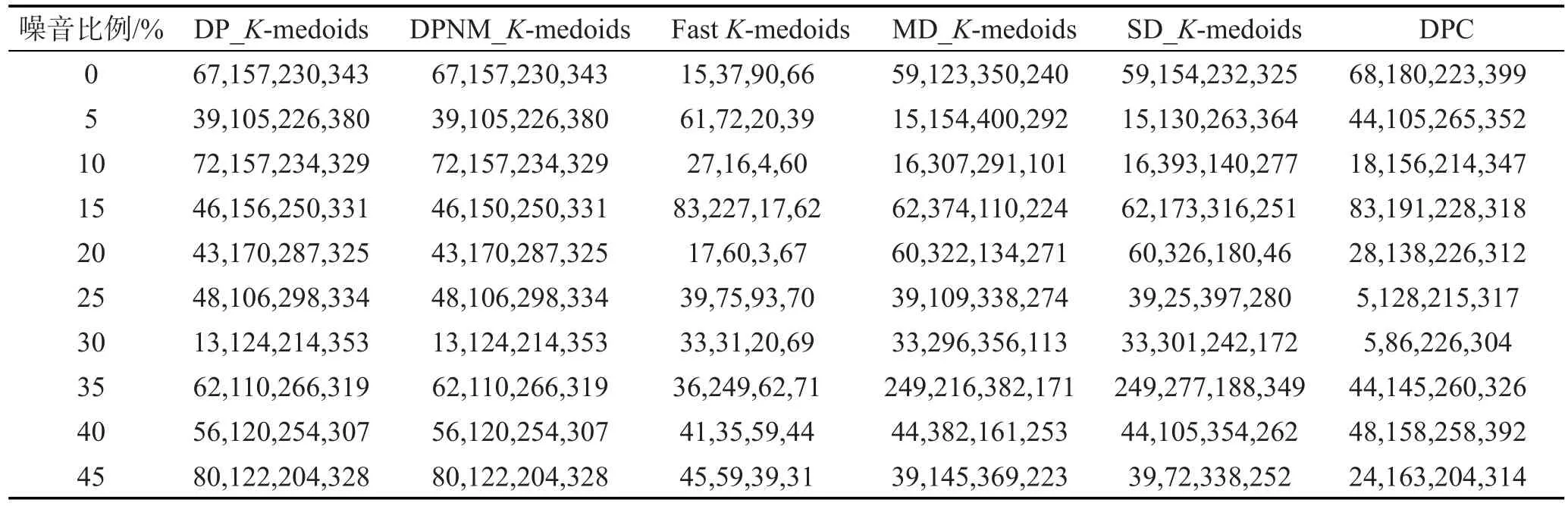
Table 5 Initial seeds selected by six algorithms on synthetic datasets with noises表5 6种算法在带噪音人工模拟数据集上选择的初始聚类中心
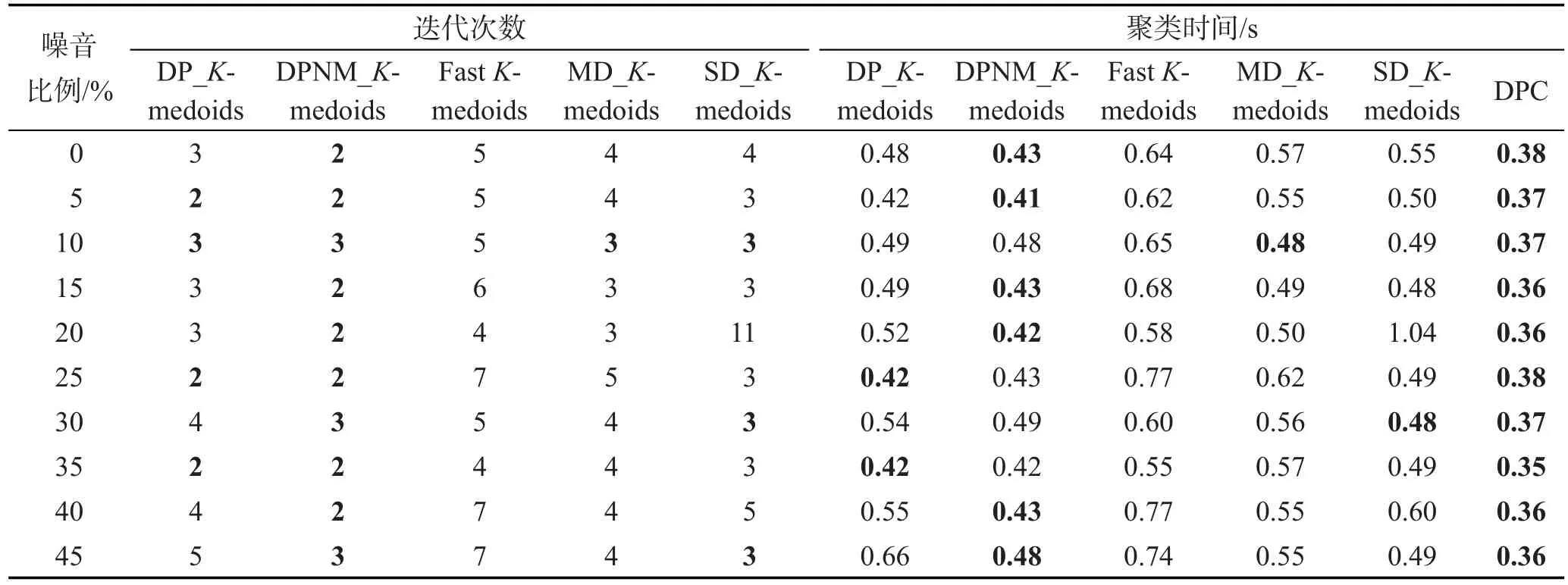
Table 6 Iterations and clustering time of six algorithms on synthetic datasets with noises表6 带噪音人工模拟数据集上6种算法的迭代次数和聚类时间
从表6中可以看出,本文DPNM_K-medoids算法在各噪音数据集的迭代次数最少。从聚类时间来看,本文两种K-medoids算法优于其他3种K-medoids算法。本文两种K-medoids算法相比,在迭代次数相同的情况下,DP_K-medoids算法聚类时间更短,因为DPNM_K-medoids算法的聚类准则函数计算更费时间。密度峰值聚类算法在带噪音人工模拟数据集上的聚类时间是6种算法中最短的,因为密度峰值聚类算法的一步分配策略使其时间消耗最低。
从图3的实验结果可以看出,本文K-medoids算法在含噪音的数据集上明显优于其他4种聚类算法。本文DPNM_K-medoids算法在含有40%噪音的人工模拟数据集上的Rand指数、Jaccard系数、Adjusted Rand index参数和聚类准确率均优于其他5种聚类算法。密度峰值聚类算法在不带噪音的人工模拟数据集的各项聚类指标最优,在噪音比例为20%、25%、35%和45%的人工模拟数据集的各项指标值最差。由此可见,本文新提出的聚类准则使得基于密度峰值点优化初始聚类中心的K-medoids算法的聚类性能更优,具有更强的鲁棒性。
综合表5、表6和图3的实验结果分析可知,本文采用密度峰值点优化初始聚类中心的K-medoids算法对噪音具有很好的鲁棒性,能发现数据集的真实类簇数和合理初始类簇中心,实现有效聚类。
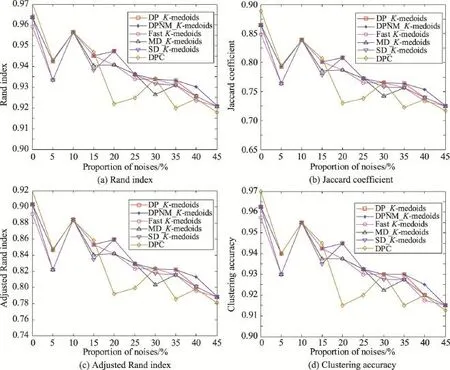
Fig.3 Rand index,Jaccard coefficient,Adjusted Rand index and clustering accuracy of six algorithms on synthetic datasets with different ratio noises图3 6种算法在不同比例噪音人工模拟数据集上的Rand指数、Jaccard系数、Adjusted Rand index参数和聚类准确率
4.2.2经典人工模拟数据集实验结果分析
本小节采用测试聚类算法性能的经典人工模拟数据集对本文提出的密度峰值优化初始聚类中心的K-medoids算法的聚类性能进行测试。实验使用的经典人工模拟数据集原始分布如图4所示。该经典人工模拟数据集的共同点是:类簇个数较多,类簇形状任意。其中S1、S2、S3和S4数据集均各含有5 000个样本,15个类簇,数据集样本重叠程度依次增加[19]。R15数据集也含有15个类簇,样本数为600[20],D31数据集含有31个类簇,样本数为3 100[20]。
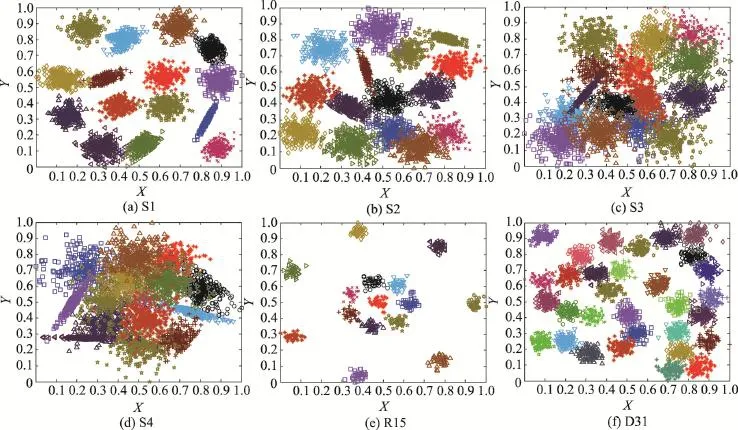
Fig.4 Original distribution of classic synthetic datasets图4 经典人工模拟数据集的原始分布

Fig.5 Decision graphs and initial seeds of two K-medoids algorithms on classic synthetic datasets图5 两种K-medoids算法对经典人工模拟数据集的决策图和初始聚类中心
在这些经典人工模拟数据集上分别运行5种K-medoids聚类算法和密度峰值聚类算法,其中本文两种K-medoids算法的最近邻样本数t取8。本文K-medoids算法确定初始聚类中心的决策图如图5所示,其中矩形框内的加粗黑圆点为初始类簇中心。MD_K-medoids算法在S1和R15数据集仅能确定出4个初始聚类中心,在S2、S3、S4和D31数据集仅能确定出5个初始聚类中心。SD_K-medoids算法在R15数据集仅能确定出4个初始聚类中心,在S1、S2、S3和D31数据集仅能确定出5个初始聚类中心,在S4数据集能确定出6个初始聚类中心。原因是:当被选为初始聚类中心的样本邻域半径过大时,使得该样本邻域内包含的样本数过多,导致剩余样本集合为空,因而无法确定足够的初始聚类中心。因此,下面将仅比较本文DP_K-medoids、DPNM_K-medoids算法、快速K-medoids算法和密度峰值聚类算法在经典人工模拟数据集上的聚类结果。4种聚类算法在S1、S2、S3、S4数据集的聚类结果分别如图6、图7、图8和图9所示。4种聚类算法在R15、D31数据集上的聚类结果分别如图10和图11所示。4种聚类算法在经典人工模拟数据集聚类结果的Rand指数、Jaccard系数、Adjusted Rand index参数和聚类准确率比较如图12所示。
从图5的实验结果可以看出,本文两种K-medoids算法在经典人工模拟数据集上识别的类簇个数与对应数据集的真实类簇数完全一致,而且决策图中的密度峰值点和非密度峰值点可以清晰分离,因此当类簇个数较多时,采用本文新定义的样本局部密度ρ和样本距离δ能准确选择密度峰值点,从而准确地确定初始聚类中心。因此,本文两种K-medoids算法在经典人工模拟数据集上能克服快速K-medoids、MD_K-medoids和SD_K-medoids算法需要人为给定初始类簇数,以及MD_K-medoids和SD_K-medoids算法当类簇个数较多时不能完全确定初始聚类中心的缺陷。
从图6至图9的实验结果可以看出,本文两种K-medoids算法和密度峰值聚类算法在S1和S2数据集的聚类结果和原始分布几乎一样,只将个别边界样本错分。本文两种K-medoids算法和密度峰值聚类算法会将S3和S4数据集中重叠区域的样本误分,非重叠区域样本能够实现正确分类。快速K-medoids算法对S1、S2、S3和S4数据集不仅将重叠区域样本分错,而且将原本属于两个类簇但是距离较近的样本聚为一类,同时还将一个类簇误分为两个类簇。由此可见,本文两种K-medoids算法和密度峰值聚类算法对S1、S2、S3和S4数据集的聚类效果优于快速K-medoids算法。
从图10和图11实验结果可知,本文K-medoids算法和密度峰值聚类算法能将R15数据集完全正确分类,将D31数据集个别重叠样本误分。快速K-medoids算法将R15数据集最中间一个类簇分为两类;将D31数据集最中间那个类簇分为3类,同时快速K-medoids算法将D31数据集原本属于多个类簇,但是距离较近的样本聚为一个类簇。因此,本文DP_K-medoids和DPNM_K-medoids算法与密度峰值聚类算法对经典人工数据集R15和D31的聚类效果远优于快速K-medoids算法对该两数据集的聚类效果。
从图12实验结果可以看出,本文DP_K-meoids和DPNM_K-medoids算法以及密度峰值聚类算法对S1、S2、S3、R15和D31数据集聚类结果的各项聚类有效性指标值均比快速K-medoids算法的相应指标值高很多,说明本文新提出的密度峰值选取初始聚类中心的K-medoids聚类方法能获得非常好的聚类结果。本文两种K-medoids算法、快速K-medoids算法和密度峰值聚类算法在S4数据集的各项聚类有效性指标值几乎相等,原因是S4数据集各类簇间样本重叠度非常高,各类簇间样本不易区分,这也是本文DP_K-meoids、DPNM_K-medoids算法和密度峰值聚类算法在S4数据集各项聚类有效性指标值偏低的原因。
综合图5~图12的实验结果分析可知,本文提出的密度峰值优化初始聚类中心的DP_K-medoids和DPNM_K-medoids算法以及密度峰值聚类算法能准确识别S1~S4、R15和D31这些经典人工模拟数据集的类簇数和合理初始聚类中心,并对这些数据集实现有效聚类。
5 结束语
本文提出了采用密度峰值优化初始聚类中心的K-medoids算法,采用样本t近邻距离之和的倒数度量样本局部密度,并定义了新的样本距离,构造样本距离相对于样本密度的决策图,选择决策图中局部密度较高且距离相对较远的样本作为初始聚类中心,自适应地识别数据集的类簇数和合理初始类簇中心,并提出新的聚类准则函数。UCI数据集实验结果揭示,本文提出的两种K-medoids聚类算法DP_K-medoids和DPNM_K-medoids在UCI真实数据集的各项聚类有效性指标优于快速K-medoids算法、MD_K-medoids算法、SD_K-medoids算法以及密度峰值聚类算法。人工模拟数据集实验结果揭示,本文两种K-medoids算法能准确发现数据集的真实类簇数和合理初始类簇中心,实现有效聚类,有效减少聚类迭代次数,缩短聚类时间,加快算法收敛速度,并对噪音有很好的鲁棒性。
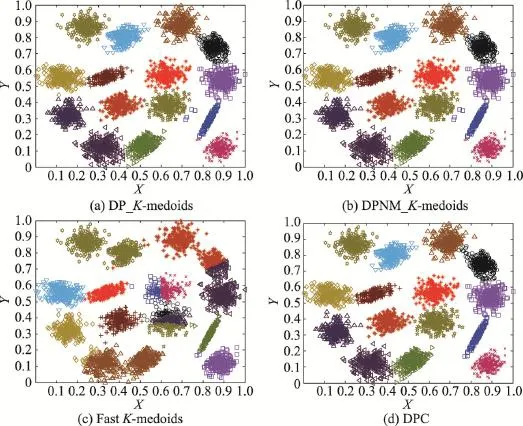
Fig.6 Clustering results of four algorithms on S1图6 4种算法在S1数据集上的聚类结果
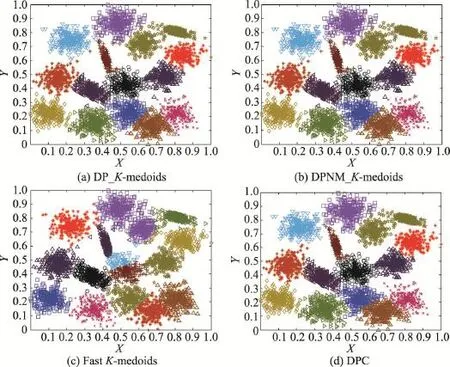
Fig.7 Clustering results of four algorithms on S2图7 4种算法在S2数据集上的聚类结果
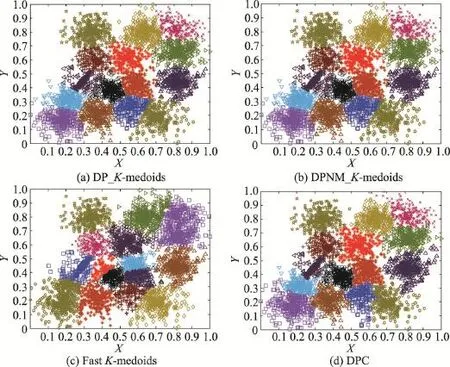
Fig.8 Clustering results of four algorithms on S3图8 4种算法在S3数据集上的聚类结果

Fig.9 Clustering results of four algorithms on S4图9 4种算法在S4数据集上的聚类结果
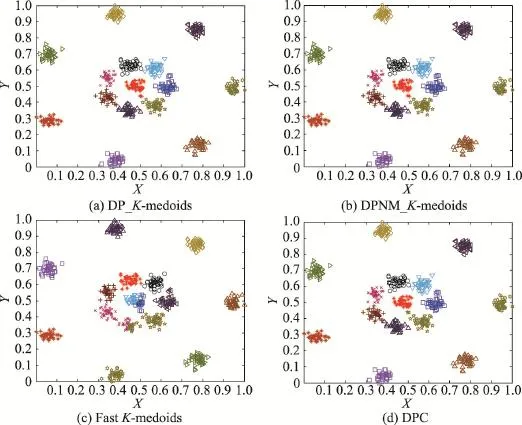
Fig.10 Clustering results of four algorithms on R15图10 4种算法在R15数据集上的聚类结果
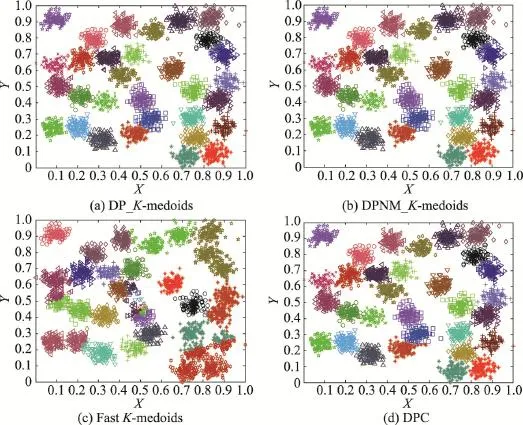
Fig.11 Clustering results of four algorithms on D31图11 4种算法在D31数据集上的聚类结果
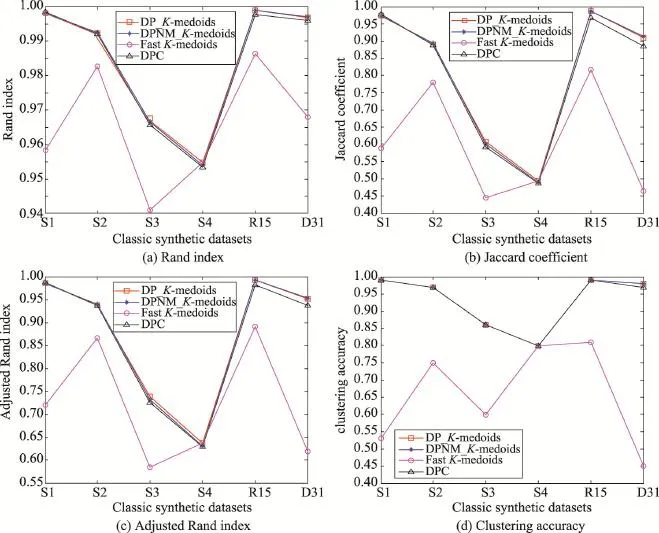
Fig.12 Rand index,Jaccard coefficient,Adjusted Rand index and clustering accuracy of four algorithms on classic synthetic datasets图12 4种算法在经典人工模拟数据集上的Rand指数、Jaccard系数、Adjusted Rand index参数和聚类准确率
References:
[1]Han Jiawei,Kamber M,Pei Jian.Data mining concepts and techniques[M].Beijing:China Machine Press,2012:398-400.
[2]MacQueen J.Some methods for classification and analysis of multivariate observation[C]//Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley,Jun 21-Jul 18,1965.Berkeley,USA:University of California Press,1967:281-297.
[3]Kaufman L,Rousseeuw P J.Finding groups in data:an introduction to cluster analysis[M].New York,USA:John Wiley&Sons,1990:126-163.
[4]Theodoridis S,Koutroumbas K.Pattern recognition[M].Boston,USA:Academic Press,2009:745-748.
[5]Park H S,Jun C H.A simple and fast algorithm for k-medoids clustering[J].Expert Systems with Applications,2009,36 (2):3336-3341.
[6]Xie Juanying,Guo Wenjuan,Xie Weixin,et al.Aneighborhoodbased K-medoids clustering algorithm[J].Journal of Shaanxi Normal University:Natural Science Edition,2012,40(4): 1672-4291.
[7]Ma Qing,Xie Juanying.New K-medoids clustering algorithm based on granular computing[J].Journal of Computer Applications,2012,32(7):1973-1977.
[8]Pan Chu,Luo Ke.Improved K-medoids clustering algorithm based on improved granular computing[J].Journal of Com-puterApplications,2014,34(7):1997-2000.
[9]Xie Juanying,Lu Xiaoxiao,Qu Yanan,et al.K-medoids clustering algorithms with optimized initial seeds by granular computing[J].Journal of Frontiers of Computer Science and Technology,2015,9(5):611-620.
[10]Xie Juanying,Gao Rui.K-medoids clustering algorithms with optimized initial seeds by variance[J].Journal of Frontiers of Computer Science and Technology,2015,9(8):973-984.
[11]Rodriguez A,Laio A.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.
[12]Rand W M.Objective criteria for the evaluation of clustering methods[J].Journal of the American Statistical Association, 1971,66(336):846-850.
[13]Zhang Weijiao,Liu Chunhuang,Li Fangyu.Method of quality evaluation for clustering[J].Computer Engineering,2005, 31(20):10-12.
[14]Yu Jian,Cheng Qiansheng.The search scope of optimal cluster number in the fuzzy clustering method[J].Science in China:Series E,2002,32(2):274-280.
[15]Yang Yan,Jin Fan,Kamel M.Survey of clustering validity evaluation[J].Application Research of Computers,2008,25 (6):1631-1632.
[16]Hubert L,Arabie P.Comparing partitions[J].Journal of Classification,1985,2(1):193-218.
[17]Vinh N X,Epps J,Bailey J.Information theoretic measures for clustering comparison:is a correction for chance necessary?[C]//Proceedings of the 26thAnnual International Conference on Machine Learning,Montreal,Canada,Jun 14-18,2009.New York,USA:ACM,2009:1073-1080.
[18]Frank A,Asuncion A.UCI machine learning repository[EB/ OL].Irvine,USA:University of California,School of Information and Computer Science(2010)[2015-03-19].http:// archive.ics.uci.edu/ml.
[19]Franti P,Virmajoki O.Iterative shrinking method for clustering problems[J].The Journal of the Pattern Recognition Society,2006,39(5):761-765.
[20]Veenman C J,Reinders M J T,Backer E.A maximum variance cluster algorithm[J].IEEE Transactions on PatternAnalysis and Machine Intelligence,2002,24(9):1273-1280.
附中文参考文献:
[6]谢娟英,郭文娟,谢维信.基于邻域的K中心点聚类算法[J].陕西师范大学学报:自然科学版,2012,40(4):1672-4291.
[7]马箐,谢娟英.基于粒计算的K-medoids聚类算法[J].计算机应用,2012,32(7):1973-1977.
[8]潘楚,罗可.基于改进粒计算的K-medoids聚类算法[J].计算机应用,2014,34(7):1997-2000.
[9]谢娟英,鲁肖肖,屈亚楠,等.粒计算优化初始聚类中心的K-medoids聚类算法[J].计算机科学与探索,2015,9(5): 611-620.
[10]谢娟英,高瑞.方差优化初始中心的K-medoids聚类算法[J].计算机科学与探索,2015,9(8):973-984.
[13]张惟皎,刘春煌,李芳玉.聚类质量的评价方法[J].计算机工程,2005,31(20):10-12.
[14]于剑,程乾生.模糊聚类方法中的最佳聚类数的搜索范围[J].中国科学:E辑,2002,32(2):274-280.
[15]杨燕,靳蕃,Kamel M.聚类有效性评价综述[J].计算机应用研究,2008,25(6):1631-1632.

XIE Juanying was born in 1971.She is an associate professor at School of Computer Science,Shaanxi Normal University,and the senior member of CCF.Her research interests include machine learning and data mining.
谢娟英(1971—),女,陕西西安人,博士,陕西师范大学计算机科学学院副教授,CCF高级会员,主要研究领域为机器学习,数据挖掘。

QU Yanan was born in 1991.She is an M.S.candidate at School of Computer Science,Shaanxi Normal University. Her research interest is data mining.
屈亚楠(1991—),女,陕西渭南人,陕西师范大学计算机科学学院硕士研究生,主要研究领域为数据挖掘。
K-medoids ClusteringAlgorithms with Optimized Initial Seeds by Density Peaks*
XIE Juanying+,QU Yanan
School of Computer Science,Shaanxi Normal University,Xi’an 710062,China
+Corresponding author:E-mail:xiejuany@snnu.edu.cn
XIE Juanying,QU Yanan.K-medoids clustering algorithms with optimized initial seeds by density peaks. Journal of Frontiers of Computer Science and Technology,2016,10(2):230-247.
To overcome the deficiencies of the fast K-medoids and the variance based K-medoids clustering algorithms whose number of clusters of a dataset must be provided manually and their initial seeds may locate in a same cluster or cannot be totally found etc.Stimulated by the density peak clustering algorithm,this paper proposes two new K-medoids clustering algorithms.The new algorithms define the local densityρiof pointxias the reciprocal of the sum of the distance betweenxiand itstnearest neighbors,and new distanceδiof pointxiis defined as well,then the decision graph of a point distance relative to its local density is plotted.The points with higher local density and apart from each other located at the upper right corner of the decision graph,which are far away from the rest points in the same dataset,are chosen as the initial seeds for K-medoids,so that the seeds will be in different clusters and the number of clusters of the dataset is automatically determined as the number of initial seeds.In order to get a better clustering,a new measure function is proposed as the ratio of the intra-distance of clusters to the interdistance between clusters.The proposed two new K-medoids algorithms are tested on the real datasets from UCI machine learning repository and on the synthetic datasets.The clustering results of the proposed algorithms are evaluated in terms of the initial seeds selected,iterations,clustering time,Rand index,Jaccard coefficient,Adjusted Randindex and the clustering accuracy.The experimental results demonstrate that the proposed new K-medoids clustering algorithms can recognize the number of clusters of a dataset,find its proper initial seeds,reduce the clustering iterations and the clustering time,improve the clustering accuracy,and are robust to noises as well.
2015-05,Accepted 2015-07.
clustering;K-medoids algorithm;initial seeds;density peak;measure function
10.3778/j.issn.1673-9418.1506072
*The National Natural Science Foundation of China under Grant No.31372250(国家自然科学基金);the Key Science and Technology Program of Shaanxi Province under Grant No.2013K12-03-24(陕西省科技攻关项目);the Fundamental Research Funds for the Central Universities of China under Grant No.GK201503067(中央高校基本科研业务费专项资金).
CNKI网络优先出版:2015-07-14,http://www.cnki.net/kcms/detail/11.5602.TP.20150714.1609.002.html
A
TP181.1

