EM最优参数求解的概率粗糙集推荐算法*

王　红，张燕平，钱付兰，陈功平

1.安徽大学 计算机科学与技术学院，合肥 230601

2.六安职业技术学院 信息与电子工程学院，安徽 六安 237158

EM最优参数求解的概率粗糙集推荐算法*

王红1,2+，张燕平1，钱付兰1，陈功平2

1.安徽大学 计算机科学与技术学院，合肥 230601

2.六安职业技术学院 信息与电子工程学院，安徽 六安 237158

WANG Hong,ZHANG Yanping,QIAN Fulan,et al.Recommendation algorithm of probability rough set based on optimal parameters of EM.Journal of Frontiers of Computer Science and Technology,2016,10(2)：285-292.

推荐系统根据用户对项目的历史评分实施推荐，评分矩阵的稀疏性导致推荐的先验知识不足，降低推荐准确率。粗糙集理论能够利用不完备知识实施有效推理，从而提出了基于人口统计学的概率粗糙集推荐模型，使用概率粗糙集理论划分等价类，降低了评分矩阵稀疏性对推荐结果的影响。使用基于最大期望（expectation maximization，EM）思想的参数求解算法求解参数α和β的最优值，将Pawlak粗糙集的边界域分解到正域或负域中，提升推荐效果。实验结果表明，概率粗糙集模型能够有效提高在评分矩阵非常稀疏情况下的推荐准确率，其在MovieLens数据集上的推荐准确率最高达到71.42%，覆盖率指标最高达到99.18%。

粗糙集；推荐算法；参数求解；最大期望（EM）算法

1　引言

网络的普及应用导致信息过载（information overload）问题[1]，用户渴望去芜存菁，让感兴趣的信息脱颖而出，减少检索时间。推荐系统（recommender system,RS）[2]不仅能够缓解信息过载问题，还能挖掘用户的潜在兴趣。网页上随处可见的“猜你喜欢”、“好友推荐”等就是推荐系统的典型应用。

推荐系统从用户的历史行为中挖掘用户兴趣从而实施推荐。一般使用评分矩阵中的分值高低刻画用户与项目之间的喜好程度关系。真实的推荐系统中由于每个用户所关注的项目数量有限，导致评分矩阵十分稀疏，这对推荐结果的准确率影响较大。

粗糙集[3]理论能够使用不完备的模糊知识实施推理。推荐系统中稀疏的评分矩阵是一种典型的不完备知识系统，为了能够在不完备的评分矩阵中实施合理的推理，提高推荐准确率，本文研究概率粗糙集理论在推荐系统中的应用。首先将评分矩阵作为概率粗糙集理论的属性库，保留评分数量最多的前n个项目的评分矩阵作为条件属性；其次采用基于最大期望（expectation maximization，EM）思想的最优参数求解算法，将F-Score评价指标作为期望值，以Pawlak粗糙集模型为起点，学习参数α、β的最优值；最后分解Pawlak粗糙集模型的边界域到正域或负域，从等价类中挖掘规则实施推荐，提高推荐的准确率。

实验表明，概率粗糙集推荐模型在MovieLens 100k数据集上的推荐准确率最高达到71.42%，覆盖率指标最高达到99.18%，比Pawlak粗糙集模型的性能更优。

本文组织结构如下：第2章介绍了推荐系统的发展及使用粗糙集理论实施推荐的相关研究；第3章详细介绍了概率粗糙集推荐模型的原理和算法；第4章使用MovieLens 100k数据集验证算法的有效性，分析实验结果；第5章总结全文并展望未来工作方向。

2　相关研究

推荐系统的任务是将用户（user）感兴趣的项目（item）按照推荐算法从项目源中筛选出来，激发用户做某件事的欲望，提高网站的访问量，增长客户浏览网站的时间。对于在线交易类网站，推荐有助于激发客户的潜在兴趣，提升销售业绩。

协同过滤推荐算法[4]（collaborative filtering，CF）根据用户的历史行为实施推荐。基于用户最近邻协同过滤推荐（UserCF）从目标用户关联的项目出发，得到兴趣相似用户集，将集合中用户感兴趣且和目标用户未关联的Top-N项目推荐给目标用户；基于项目的最近邻推荐算法（ItemCF）先计算项目间的相似度，然后根据项目的相似度和用户的历史行为生成推荐列表。

基于人口统计学的推荐算法是协同过滤推荐算法的扩展，从大量用户的历史行为中学习规则实施推荐，属于统计推理范畴[5]。本文提出的概率粗糙集模型中的等价类（条件属性）和决策属性就采用统计推理原理，借助集群智慧，根据用户的个人属性完成推荐。

粗糙集的经典模型为Pawlak模型，仅考虑模型中绝对正确的正负域，不考虑正确与错误参半的边界域[6]，而在实际应用中，合理利用边界域能够达到更理想的效果[7]。概率粗糙集模型[8-9]使用α、β参数来分解边界域到正域或负域，常用的概率粗糙集模型有决策理论粗糙集模型[10]、贝叶斯粗糙集模型[11]、变精度粗糙集模型[12]等。

近几年，粗糙集理论在推荐系统研究领域得到了较多的关注。Kudo等人[13]通过用户的历史查询数据构造粗糙集决策规则，推荐满足决策规则的产品给用户，在构造粗糙集过程中仅利用用户自身的历史数据，没有考虑协同推荐的融合；Kashima等人[14]通过用户对菜单的选择形成简单规则实施推荐；Azam等人[15]采用博弈理论训练推荐模型的参数，将推荐精度和一般性指标作为博弈理论的双方，以得到合适的参数值。参数学习和推荐时没有考虑数据稀疏性问题，仅从MovieLens数据集中随机选择10部访问量较高的电影进行10倍交叉实验，验证算法有效性，没有考虑到全数据集的推荐应用问题，也没有提到粗糙集中属性约简方法，对于算法的下一步应用没有提出解决策略。

3　概率粗糙集推荐模型

为了解决Pawlak粗糙集模型不能容错的问题，概率粗糙集模型是利用集合X与边界域等价关系的重叠度，借助参数α、β细化Pawlak粗糙集模型的边界域而得到的新模型[16]。

当参数α=1，β=0时，概率粗糙集模型转化为Pawlak粗糙集模型；当α＜1时，Pawlak粗糙集模型中的一部分边界域将划分到正域中，当β＞0时，一部分边界域将划分到负域中，将Pawlak粗糙集模型转化为概率粗糙集模型[17]。

3.1基于概率粗糙集的推荐

基于概率粗糙集的推荐要先从信息表中训练出决策表，然后从决策表中获得推荐策略实施推荐。表1是一个小数量的用户对电影的评价矩阵，可看作一张信息表，这里将电影1～电影3的评价作为条件属性，电影4的评价作为决策属性。

Table 1　Rating of movies表1　电影评分表

3.1.1划分等价关系

将条件属性值相同的用户划分到同一等价类中，划分结果如表2的第1列所示。

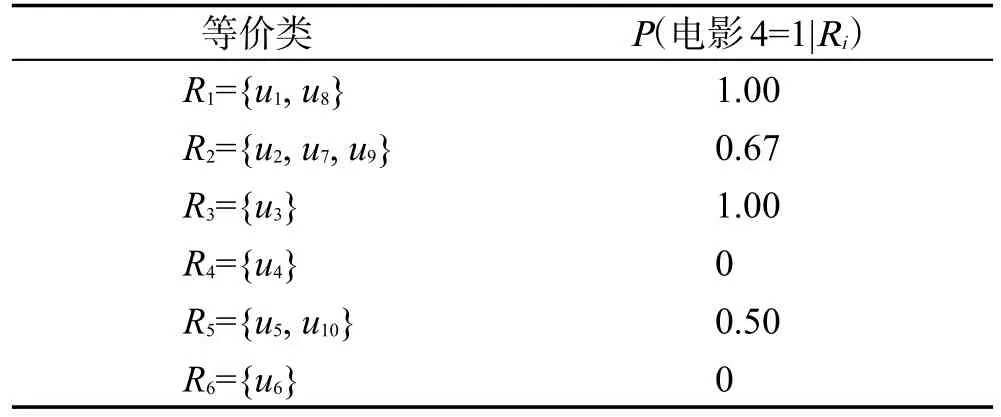
Table 2　Equivalence class partitioning and conditional probability calculation based on Table 1表2　基于表1的等价类划分及条件概率计算

3.1.2计算条件概率

由表1可得出R1类对电影4的评分全部为1，即R1等价类对电影4评分为1的概率为100%，若有新用户划分到R1，基于人口统计学的统计推理认为新用户对电影4评分为1的概率是100%；R2对电影4的评分为1的概率为2/3=66.67%。以此类推，得到电影4的决策表如表3所示。

3.1.3选择评价指标

推荐系统的评价指标有很多，如召回率（Recall）、准确率（Precision）、覆盖率（Coverage）、F-Score等，鉴于粗糙集推荐的特殊性，以准确率、覆盖率以及两个指标为参数的F-Score值作为评价指标[18]，计算公式为：

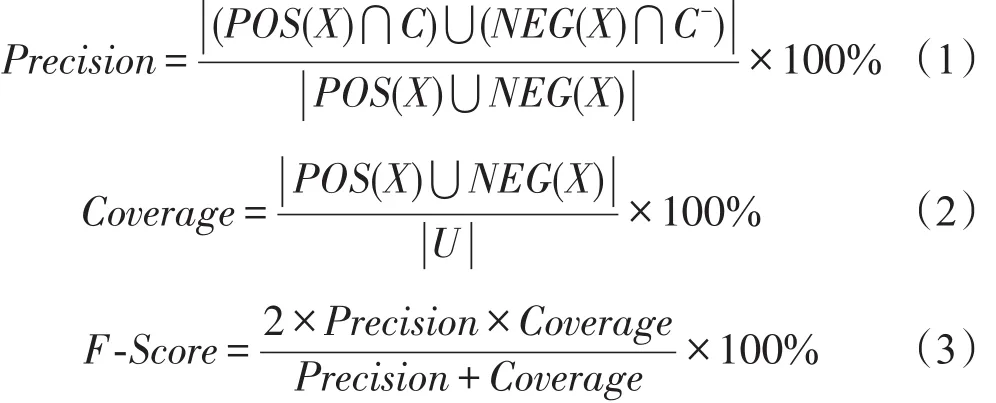
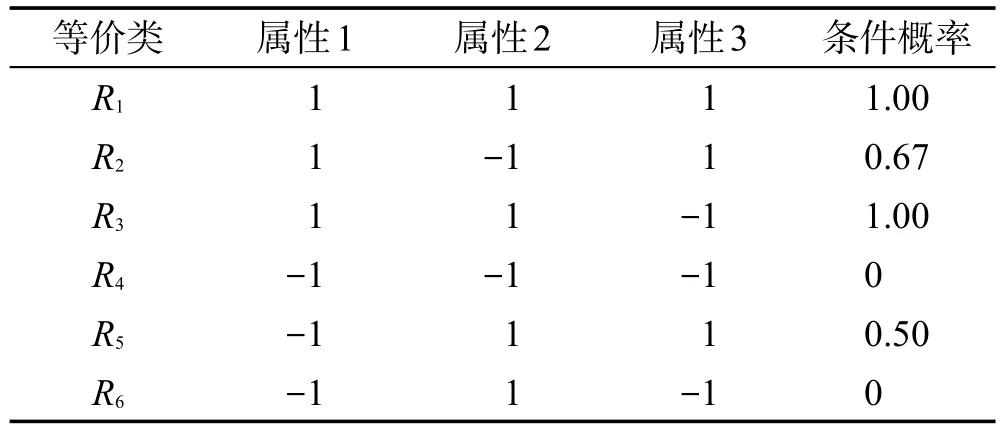
Table 3　Decision table of Movie 4表3　电影4的决策表

其中，C表示正域的预测结果集，C-表示负域的预测结果集，若C集合值取1，则C-集合值取-1。

准确率体现推荐的正确概率，覆盖率体现推荐的广度，若覆盖率为100%，表示边界域全部被划分到正域或负域中。

对于决策表3，当α=1，β=0时，正域、负域和边界域分别为POS1,0(X)=R1⋃R3，NEG1,0(X)=R4⋃R6，BND1,0(X)=R2⋃R5，根据式（1）和（2），Precision= 100%，Coverage=50%，即推荐的准确率为100%，但只能为50%的用户实施推荐，另外的50%用户因处于边界域而无法实施推荐，F-Score=0.67。

当α=0.5，β=0.5时，POS0.5,0.5(X)=R1⋃R2⋃R3⋃R5，NEG0.5,0.5(X)=R4⋃R6，BND0.5,0.5(X)=φ，此时Precision=86.7%，Coverage=100%，牺牲13.3%的准确率，提高50%的推荐广度，F-Score=0.93。

因此为了提升推荐效果，在实际应用时，α、β参数需要通过学习获得具体取值。

3.2基于EM思想的最优参数求解算法

3.2.1推荐流程

全数据集下的概率粗糙集模型训练流程如图1所示。其中求解参数α、β的最优解是提升推荐效果的关键步骤。

Fig.1　Training flow chart of probabilistic rough set recommendation model图1　概率粗糙集推荐模型的训练流程图

3.2.2基于EM思想的最优参数求解算法

EM算法[19]是一种求解参数最大似然估计的迭代算法，在参数估计求解中应用广泛。这里使用EM算法思想求解使得F-Score值最优时的α、β参数值。

以Pawlak粗糙集模型为起点，即α、β的初始值为1和0，将项目i在参数α、β下的F-Score值定义为EM算法中的E步骤，即将F-Score作为期望值，求解使得F-Score值最高时的α、β值。

要使得F-Score值最优，可降低参数α值和增加参数β值。这里M步骤的作用就是慢慢改变初始参数值，分解边界域，分为3种选择，F1=F-Score(α↓)，降低α时的期望值；F2=F-Score(β↑)，增加β时的期望值；F3=F-Score(α↓β↑)，降低α且增加β时的期望值。然后将F1、F2、F3中期望值最优且高于当前FScore值的参数重新赋值给α、β，具体如下。

E步骤 根据式（3）计算F=F-Score(α,β)。

M步骤 根据式（3）和参数改变速率Radio计算F1，F2，F3的值。

Radio控制α、β参数降低和增加的速率，求解α、β参数最优值的算法如下所示。

算法1基于EM思想的参数求解算法

4　实验结果与分析

使用MovieLens 100k数据集验证文中所提出的基于概率粗糙集的推荐，该数据集是由GroupLens工作小组发布的可用于数据挖掘、推荐系统等科研领域的数据集，电影评分记录约10万条，每条评分记录由用户id、电影id和评分值组成，评分值可取1到5的整数，数据集简介如表4所示。

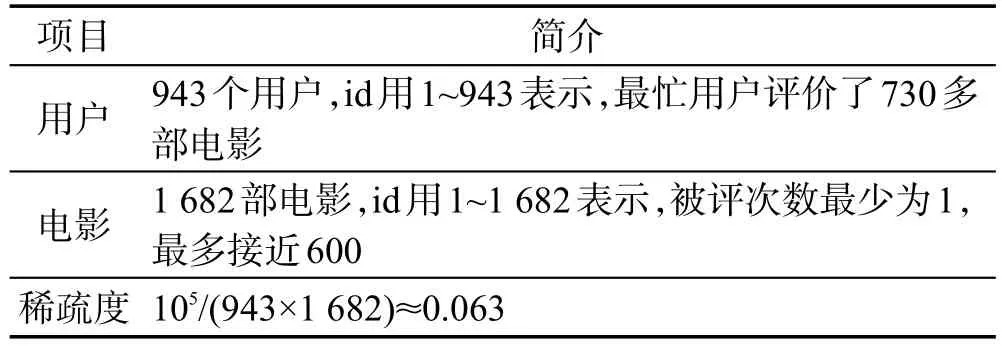
Table 4　Data set introduction of MovieLens表4　MovieLens数据集简介

将电影评分表按照用户id排序再以每用户8∶2的比例划分为训练集Train和测试集Test，因部分电影的评分记录少，可能只在训练集或测试集中出现。

4.1条件属性个数n

从Train中提取电影1的评价矩阵，Train(1)有350行、1 682列有效数据，Train(50)有468行、1 682列有效数据，按照算法1中等价类的学习规则，条件属性个数n与等价类数量的关系如表5所示。

Table 5　Relationship betweennand the number of equivalent classes表5　n与等价类数量的关系

n=15时，等价类数与Train(i)的行数差值很小，划分的集合粗糙度小；n=5时，等价类数量与Train(i)的行数差值较大，划分集合的粗糙度相对较高。综上，n取5～10之间的值较合理。

4.2测试结果与分析

评分值可取1到5的整数，将5级评分简化为2级评分，设置划分值γ，第1组γ=3，即1、2、3分标记为-1，4、5分标记为1；第2组γ=4，即1、2、3、4分标记为-1，5分标记为1。

4.2.1不同n值的实验

表6是γ=4时不同n值下的推荐效果比较。

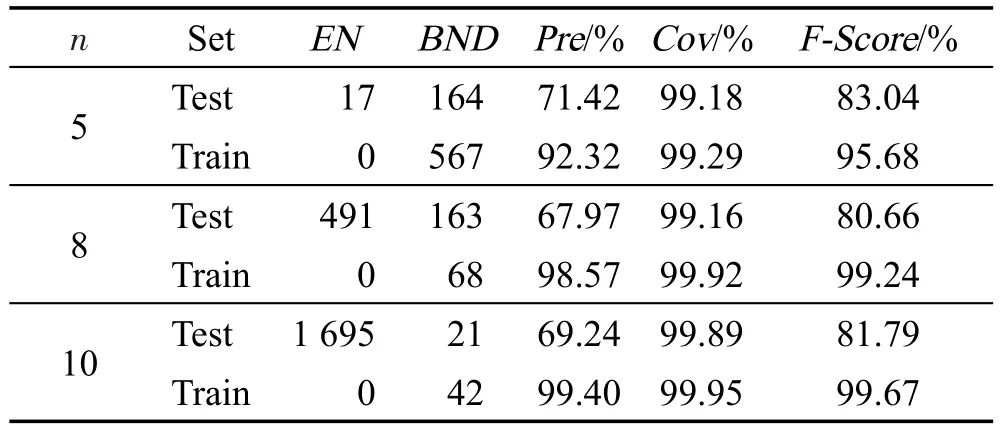
Table 6　Recommended effect of γ=4表6　γ=4的推荐效果

表6中“EN”列表示在决策表中找不到等价类的项目数，“BND”列表示在决策表中能找到等价类，但处于边界域的项目数，Pre、Cov分别表示准确率和覆盖率。由表6可见，n值越大，找不到等价类的记录越多，当n=5时，测试集Test的总体评价值最优，经验证，对其他划分值n取5时评价值都是最优，后文无特别说明n值取5。

4.2.2不同γ值的实验

图2是两组实验中Test和Train集合推荐效果比较，当划分值取4时Test集合的推荐准确度为71.42%，取3时只有58.77%，整个模型的覆盖率指标都非常高，即几乎可以为所有用户实施推荐。

4.2.3不同推荐模型的实验

由第3章可知，Pawlak粗糙集模型可以使训练集的推荐准确率达到100%，但覆盖率是最低的。表7是Train集合在概率粗糙集推荐模型与Pawlak粗糙集模型下的3项指标值。

表7中A表示“Pawlak粗糙集模型”，B表示“概率粗糙集模型”，由数据可见，准确率差值较小，最大达到11.92%，覆盖率差值较大，最大达到33.29%，因此Train集合的概率粗糙集推荐模型和综合指标优于Pawlak粗糙集模型。

图3更直观地体现了Train集合在不同推荐模型下的各项指标比较。

Fig.2　Recommended effect of different γ图2　不同γ值的推荐效果

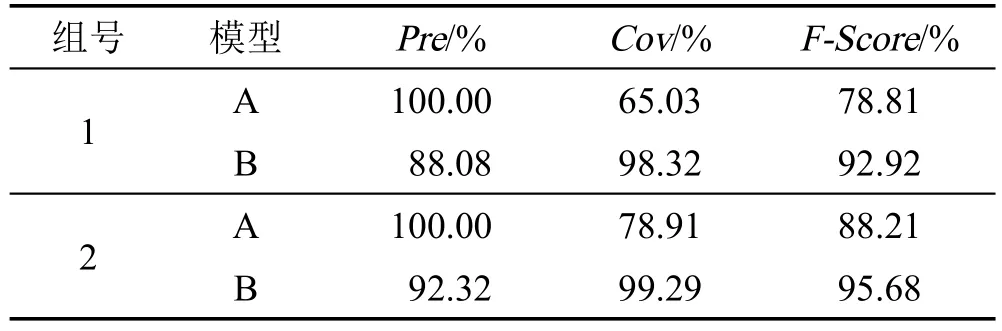
Table 7　Recommended effect of Train set under different models表7　Train集合在不同推荐模型下的效果

Fig.3　Recommended effect of Train set under different models图3　Train集合在不同推荐模型下的效果

表8是Test集合在不同模型下的3项指标值。

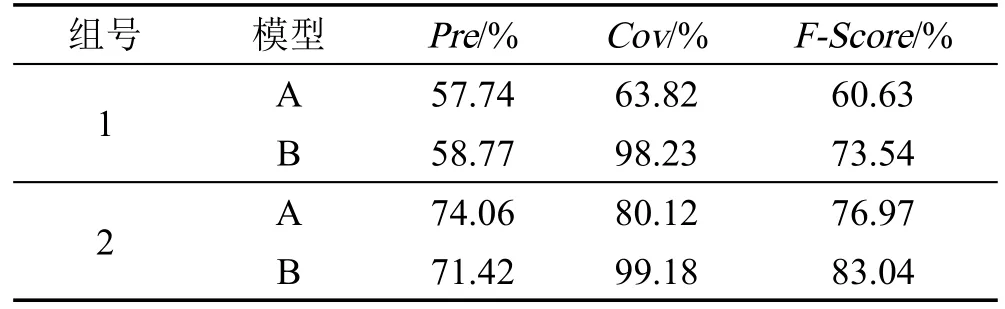
Table 8　Recommended effect of Test set under different models表8　Test集合在不同推荐模型下的效果

与Train集合一样，在划分值相同时，准确率差值较小，最大差值不到3.00%，覆盖率差值最大达到34.41%，因此Test集合的概率粗糙集模型和综合指标优于Pawlak粗糙集模型。

图4是Test集合在两种推荐模型下的各项指标比较。

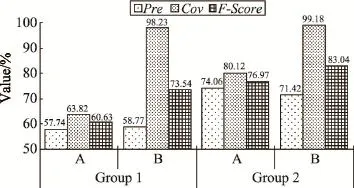
Fig.4　Recommended effect of Train set under different γ图4　Test集合的不同γ值的推荐效果

5　结束语

概率粗糙集推荐模型可以降低评分矩阵稀疏性对推荐精度的影响，α、β参数将粗糙集中的边界域合理地分配到正域或负域中，基于EM思想的参数学习算法能够很好地找到使得当前项目F-Score值最优的参数值。在基于粗糙集理论的推荐算法中，处于边界域的等价类是无法实施推荐的，为了进一步提高准确率和覆盖率，可以和协同过滤推荐算法结合，这将是下一步研究的内容。当前模型只能对两级评分模式实施推荐，如何扩展到多级评分模式也将是模型今后要解决的问题。

References:

[1]Cao Hongjiang,Fu Kui.Research on clustering search method in collaborative filtering recommendation system[J].Computer Engineering andApplications,2014,50(5):16-20.

[2]Sun Guangfu,Wu Le,Liu Qi,et al.Recommendations basedon collaborative filtering by exploiting sequential behaviors[J]. Journal of Software,2013,24(11):2721-2733.

[3]Wang Guoyin,Yao Yiyu,Yu Hong.A survey on rough set theory and its application[J].Chinese Journal of Computers, 2009,32(7):1229-1246.

[4]Lin Hongli,Yang Xuedong,Wang Weisheng.A contentboosted collaborative filtering algorithm for personalized training in interpretation of radiological imaging[J].Journal of Digital Imaging,2014,27(4):449-456.

[5]Jiao Dongjun.Collaborative filtering algorithm based on user demographics and expert opinions[J].Computer Engineering &Science,2015,37(1):179-183.

[6]Guan Lihe,Wang Guoyin,Yu Hong.Incremental algorithm of Pawlak reduction based on attribute order[J].Journal of Southwest Jiaotong University,2011,46(3):461-468.

[7]Ma Xi’ao,Wang Guoyin,Yu Hong,et al.Decision region distribution preservation reduction in decision-theoretic rough set model[J].Information Sciences,2014,278(10): 614-640.

[8]Yao Yiyu.Probabilistic rough set approximations[J].International Journal of Approximate Reasoning,2007,49(2): 255-271.

[9]Azam N,Yao Jingtao.Analyzing uncertainties of probabilistic rough set regions with game-theoretic rough sets[J].Elsevier Journal,2014,55(1):142-155.

[10]Guo Min,Jia Xiuyi,Shang Lin.Decision-theoretic rough set attribute reduction and classification based on fuzzification[J]. Pattern Recognition and Artificial Intelligence,2014,27(8): 701-707.

[11]Śle¸zak D,Ziarko W.The investigation of the Bayesian rough set model[J].International Journal of Approximate Reasoning,2005,40(1):81-91.

[12]Yang Yanyan,Chen Degang,Dong Ze.Novel algorithms of attribute reduction with variable precision rough set model[J]. Neurocomputing,2014,139(2):336-344.

[13]Kudo Y,Amano S,Seino T,et al.A simple recommendation system based on rough set theory[J].KANSEI Engineering International,2010,6(3):19-24.

[14]Kashima T,Matsumoto S,Ishii H.Decision support system for menu recommendation using rough sets[J].International Journal of Innovative Computing,Information and Control, 2011,7(5B):2799-2808.

[15]Azam N,Yao Jingtao.Game-theoretic rough sets for recommender systems[J].Knowledge-Based Systems,2014,72: 96-107.

[16]Wang Lei,Li Tianrui.Matrix-based computational method for upper and lower approximations of rough sets[J].Pattern Recognition and Artificial Intelligence,2011,24(6): 756-762.

[17]Wang Guoyin,Zhang Qinghua.Uncertainty of rough sets in different knowledge granularities[J].Chinese Journal of Computers,2008,31(9):1588-1598.

[18]Zhu Yangyong,Sun Jing.Research and development on recommender system[J].Journal of Frontiers of Computer Science and Technology,2015,9(5):513-525.

[19]Wang Ge,Yu Hongyi,Shen Zhixiang,et al.A fast convergence parameter estimation method based on expectation maximum(EM)algorithm[J].Journal of Jilin University: Engineering and Technology Edition,2013,43(2):532-537.

附中文参考文献：

[1]曹洪江,傅魁.协同过滤推荐系统中聚类搜索方法研究[J].计算机工程与应用,2014,50(5):16-20.

[2]孙光福,吴乐,刘淇,等.基于时序行为的协同过滤推荐算法[J].软件学报,2013,24(11):2721-2733.

[3]王国胤,姚一豫,于洪.粗糙集理论与应用研究综述[J].计算机学报,2009,32(7):1229-1246.

[5]焦东俊.基于用户人口统计与专家信任的协同过滤算法[J].计算机工程与科学,2015,37(1):179-183.

[6]官礼和,王国胤,于洪.属性序下的增量式Pawlak约简算法[J].西南交通大学学报,2011,46(3):461-468.

[10]郭敏,贾修一,商琳.基于模糊化的决策粗糙集属性约简和分类[J].模式识别与人工智能,2014,27(8):701-707.

[16]王磊,李天瑞.基于矩阵的粗糙集上下近似的计算方法[J].模式识别与人工智能,2011,24(6):756-762.

[17]王国胤,张清华.不同知识粒度下粗糙集的不确定性研究[J].计算机学报,2008,31(9):1588-1598.

[18]朱扬勇,孙婧.推荐系统研究进展[J].计算机科学与探索, 2015,9(5):513-525.

[19]王戈,于宏毅,沈智翔,等.一种基于EM算法的快速收敛参数估计方法[J].吉林大学学报:工学版,2013,43(2): 532-537.

王红（1983—），女，安徽霍邱人，2011年于安徽大学获得硕士学位，现为六安职业技术学院讲师，主要研究领域为个性化推荐，数据库技术。

ZHANG Yanping was born in 1962.She is a professor and Ph.D.supervisor at School of Computer Science and Technology,Anhui University.Her research interests include quotient space and intelligent computing.

张燕平（1962—），女，安徽巢湖人，安徽大学计算机与科学技术学院教授、博士生导师，主要研究领域为商空间，智能计算。

钱付兰（1978—），女，安徽蚌埠人，2005年于安徽大学获得硕士学位，现为安徽大学博士研究生，CCF会员，主要研究领域为社交网络，个性化推荐。

陈功平（1980—），男，安徽六安人，2012年于合肥工业大学获得硕士学位，现为六安职业技术学院讲师，主要研究领域为个性化推荐，网络技术。

Recommendation Algorithm of Probability Rough Set Based on Optimal Parameters of EM*

WANG Hong1,2+,ZHANG Yanping1,QIAN Fulan1,CHEN Gongping2
1.School of Computer Science and Technology,Anhui University,Hefei 230601,China
2.College of Information and Electronic Engineering,Lu’an Vocation Technology College,Lu’an,Anhui 237158,China
+Corresponding author:E-mail:wh0115140@126.com

Recommender systems recommend items to users according to the historical ratings of items.Used to express these historical ratings,the rating matrix usually has the character of sparsity which can lead to the lack of prior knowledge and the decrease of recommendation accuracy.Rough set theory can use incomplete knowledge to effectively reasoning.This paper proposes a recommendation model of probability rough set based on demographic, which is equivalent to the classification of rough set theory,and reduces the effect of sparsity of the rating matrix. This paper uses EM(expectation maximization)algorithm to solve the optimal parameters of α and β,decomposes the Pawlak boundary region into the positive or negative domains according to the parameters,and promotes the recommendation effect.The experimental results show that the probability rough set model can effectively improve therecommendation accuracy.And the recommendation accuracy reaches 71.42%,and the coverage rate reaches 99.18% in the MovieLens test set.

2015-06,Accepted 2015-08.

rough set;recommendation algorithm;solving paramaters;expectation maximization(EM)algorithm

WANG Hong was born in 1983.She the M.S.degree from Anhui University in 2011.Now she is a lecturer at Lu’an Vocation Technology College.Her research interests include personalized recommendation and database technology.

QIAN Fulan was born in 1978.She the M.S.degree from Anhui University in 2005.Now she is a Ph.D. candidate at Anhui University,and the member of CCF.Her research interests include social networks and personalized recommendation.

CHEN Gongping was born in 1980.He the M.S.degree from Hefei University of Technology in 2012. Now he is a lecturer at Lu’an Vocation Technology College.His research interests include personalized recommendation and network technology.

10.3778/j.issn.1673-9418.1506015

*The Humanities and Social Sciences Youth Fund of Ministry of Education of China under Grant No.14YJC860020(教育部人文社科青年基金项目);the Higher School Youth Talent Support Plan of Anhui Province in 2014(安徽省2014年高校优秀青年人才支持计划);the Natural Science Research Project of Higher School of Anhui Province under Grant No.KJ2015A435(安徽省高校自然科学研究重点项目);the Higher School Youth Talent Support Plan Key Project ofAnhui Province in 2016 under Grant No.gxyqZD2016570 (安徽省2016年高校优秀青年人才支持计划重点项目).

CNKI网络优先出版：2015-08-12,http://www.cnki.net/kcms/detail/11.5602.TP.20150812.1634.006.html

A

TP301