面向大规模数据的快速多代表点仿射传播算法*
刘 季,陈秀宏,杭文龙
江南大学 数字媒体学院,江苏 无锡 214122
面向大规模数据的快速多代表点仿射传播算法*
刘季+,陈秀宏,杭文龙
江南大学 数字媒体学院,江苏 无锡 214122
LIU Ji,CHEN Xiuhong,HANG Wenlong.Fast multi-exemplar affinity propagation algorithm for large data sets.Journal of Frontiers of Computer Science and Technology,2016,10(2):268-276.
针对原始的仿射传播(affinity propagation,AP)聚类算法难以处理多代表点聚类,以及空间和时间开销过大等问题,提出了快速多代表点仿射传播(multi-exemplar affinity propagation using fast reduced set density estimator,FRSMEAP)聚类算法。该算法在聚类初始阶段,引入快速压缩集密度估计算法(fast reduced set density estimator,FRSDE)对大规模数据集进行预处理,得到能够充分代表样本属性的压缩集;在聚类阶段,使用多代表点仿射传播(multi-exemplar affinity propagation,MEAP)聚类算法,获得比AP更加明显的聚类决策边界,从而提高聚类的精度;最后再利用K-邻近(K-nearest neighbor,KNN)算法分配剩余点得到最终的数据划分。在人工数据集和真实数据集上的仿真实验结果表明,该算法不仅能在大规模数据集上进行聚类,而且具有聚类精度高和运行速度快等优点。
仿射传播;聚类;大数据;多代表点
1 引言
聚类是将物理或者抽象对象的集合依据对象的相似性分成多个类别的过程,使得同一个类别中的对象之间具有较高的相似度,而不同类别中的对象具有较低的相似度。在机器学习中,聚类是一种很重要的无监督学习方法[1]。
Frey等人在Science上首次提出了仿射传播(affinity propagation,AP)聚类算法[2]。它引入数据点间的消息传递机制,通过数据集中数据点之间的消息传递获得具有更高价值的聚类中心点,提高了聚类的质量。AP算法无需预先设置类别数,而且相比K-means等经典算法具有聚类效果好和错误率低等优点[3],在图像处理、数据挖掘等领域成为研究热点。为反映数据的实际分布特性,文献[4]设计了一种可变相似性度量的计算方法,解决了多重尺度及任意空间形状的数据聚类处理。文献[5]先引入元点(meta-point)将标记的数据与未标记的数据形成成对约束条件,再将违背成对约束条件的惩罚项加入目标函数,实现了AP的半监督过程。文献[6]将AP算法成功应用于增值聚类模型中,实现了向动态数据聚类的扩展。文献[7]先对图像进行超像素分割,通过计算这些超像素之间的全模糊连接度计算相似度,用AP算法完成了无监督图像分割。AP算法在以上多个领域获得了成功,但是由于AP算法中每一个类用一个代表点表示,使得它在多代表点模型中的应用受到了极大阻碍[8],于是文献[8]提出多代表点仿射传播(multi-exemplar affinity propagation,MEAP)聚类算法,允许一个类用多个代表点进行表示,最后推举出属于此类的超级代表点,通过改变消息迭代过程成功地实现了AP在多特征模型中的应用。虽然MEAP算法成功应用在了多代表点模型中,聚类边界比AP更加精确,但忽略了消息参数的迭代造成的繁重的时间开销,因此该方法不适用于处理大规模数据集。
本文提出了一种基于大规模数据集的快速多代表点仿射传播聚类算法(multi-exemplar affinity propagation using fast reduced set density estimator, FRSMEAP),该算法在聚类之前利用基于核心集的中心约束最小包含球的快速压缩方法(fast reduced set density estimator,FRSDE)对原始大规模数据集进行压缩,得到可以代表整个数据集的压缩集,再对该压缩集使用MEAP算法得到全局聚类中心,最后采用K-邻近(K-nearest neighbor,KNN)算法得到最终划分,从而解决了复杂模型大数据集下的聚类问题。
2 经典的仿射传播聚类算法
AP算法是一种无预设类别数的聚类方法,它将所有的数据点都作为潜在的代表点,以数据之间的相似度矩阵作为输入,通过吸引度矩阵和归属度矩阵之间的迭代计算,不断更新数据之间的消息,最终选出聚类中心。设给定的数据集为X={x1,x2,…,xN},数据xi与xk之间的相似度为,吸引度为r(i,k),归属度为a(i,k),则与X对应的相似度矩阵、吸引度矩阵和归属度矩阵分别为S=[s(i,k)]N×N,R=[r(i,k)]N×N和A=[a(i,k)]N×N。AP算法的核心是对R和A中元素(又称为消息参数)的交替更新。
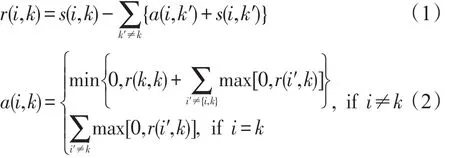
对于任意数据xi,迭代最后它所在类的代表点为,将具有相同类代表点的数据聚为同一个类。
3 基于大数据集的快速多代表点仿射传播聚类算法
3.1多代表点的仿射传播聚类算法
AP算法以每个点作为潜在的代表点,故它难以应用于诸如场景分析和特征识别等多特征模型[9]。MEAP算法对AP算法中的消息传递及其迭代过程进行改进,以便能适用于多代表点数据模型。它将每个数据点分配给最合适的代表点,而选出的代表点又被分配给最合适的超级代表点,这样就能得到最后的聚类中心。
若G=[gij]N×N为分配矩阵,其中gij=1表示数据xi选择数据xj作为代表点,而gii=k,k∈{1,2,…,N}表示代表点xi的超级代表点为xk。MEAP方法的目标是求使 S(G)=S1+S2达到最大的最优分配,那么G*中主对角线上的元素即为最后的聚类中心,其中表示各个数据点相对应的代表点之间的相似度之和,表示各个代表点相对应的超级代表点之间的相关度之和,而l(i,j)=s(i,j)/N表示代表点xi与其潜在超级代表点xj之间的关联程度,矩阵称为关联矩阵。由于极大化目标函数S(G)是一个NP难问题,采用置信传播(belief propagation,BP)中的max-sum方法[10]来表示数据点、代表点和超级代表点之间的消息传递。当i≠j(i=1,2,…,N,j=1,2,…,N)时:
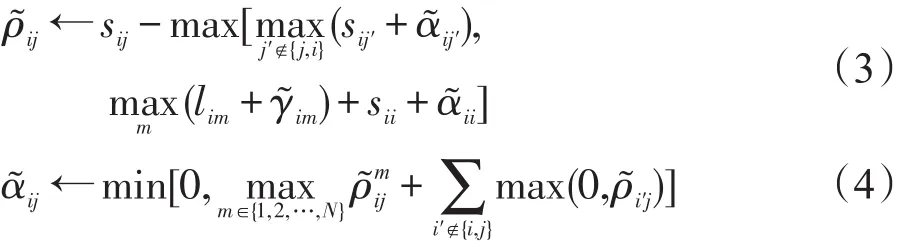
而对i=1,2,…,N,k=1,2,…,N有:


MEAP算法扩大了聚类决策边界,在不考虑关联矩阵L的情况下它退化为AP算法。由于MEAP算法中增加了4条消息传递函数,而每条消息函数的时间复杂度为Ο(N2lbN),故其存储和时间复杂度大大增加,从而限制了其在大规模数据集上的应用。
3.2FRSMEAP算法
MEAP算法在面向大规模数据集时,时空效率低。本文使用快速压缩集密度估计(FRSDE)对原始大规模数据样本进行压缩,使得压缩后数据集的密度估计与原数据集近似,较好地保持了数据集的特性,能从根本上减少MEAP聚类过程的样本数据,从而减小算法的时间开销,同时兼顾MEAP聚类的优点,很好地平衡了时间与精度之间的矛盾。
文献[11]提出压缩集密度估计器(reduced set density estimator,RSDE),文献[12]进一步揭示了RSDE与核化中心约束极小化包含球(center-constrained minimal enclosing ball,CCMEB)问题之间的等价关系,利用快速核心集技术[13]求解CCMEB问题,得到具有与原始数据集近似的核密度估计函数的目标压缩数据集,提出了FRSDE。为增强算法的适用性,在FRSDE算法中引入非线性函数映射φ(x)将低维数据映射到高维空间特征Γ,并在特征空间中寻求以为中心的最小包含球(minimal enclosing ball,MEB),其中δ∈R,c为Γ中特征向量。在数据子集Q⊆X上CCMEB问题可表示为:

其对偶形式为:
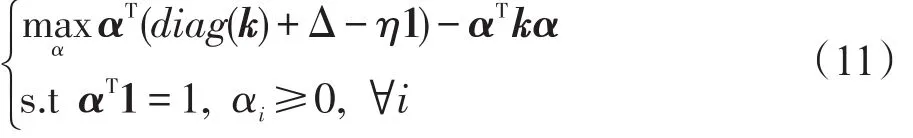
其中,α为p维Lagrange乘子向量;1=[1,1,…,1]T为p维列向量;K=[k(xi,xj)]=[φ(xi)Tφ(xj)]为Q上的 p×p维核矩阵,p为Q中数据个数。设问题(11)关于Q的最优解为α*,则与Q相关的最小包含球半径R*和中心c*分别为:

特征空间Γ′中任一个点到球心的距离平方为:
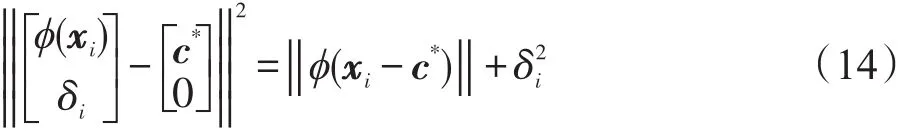
核心集之间采用高斯核作为核函数进行核密度估计,FRSDE方法通过不断扩大核心集,最后得到包含X的最小包含球的核心集,此时由所对应的数据而组成的集合Xr称为FRSDE的压缩集。

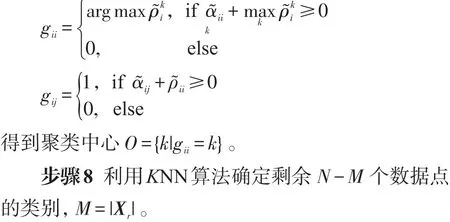
MEAP算法中每条消息的传递都可能出现震荡,为了消除出现的震荡,在步骤7的消息参数传递过程中引入阻尼系数λ,μ=λμold+(1-λ)μnew,μ代表7条消息参数中的任意一条,λ越大消除震荡的效果越好,但是算法的收敛速度会减慢。
3.3算法复杂性分析
在MEAP算法中,每条消息参数每次迭代的时间复杂度为Ο(N2lbN),令迭代次数为ρ,MEAP的时间复杂度为Ο(ρN2lbN)。在FRSMEAP算法中,步骤3求离中心点ct最远点时,每次迭代的时间复杂度为,其中为寻找最远点的目标域样本规模,当样本规模N较大时非常耗时。此时文献[14]通过在中随机抽取子集来寻找最远点,当子集规模时最远点在中的概率约为95%,这样复杂性降为。类似于FRSDE算法[12],步骤4中利用核心集求解问题(11)的时间复杂度为Ο(N′/ε2+1/ε4),其中N′为核心集中样本数,ε为逼近参数,由于N′<<N,故该复杂性也远小于求解所有样本的时间复杂性。对压缩集Xr进行聚类的时间复杂性为Ο(dM2lbM),其中d为迭代次数;分配剩余点的时间复杂性为Ο(N-M)。这样,FRSMEAP算法总的时间复杂性上界为Ο(N/ε2+ 1/ε4+dM2lbM+N-M),M<<N,它与总样本数N成线性关系。
综上可见,FRSMEAP算法的复杂性远小于MEAP算法的复杂性,其运算速度得到很大的提高,从而能解决MEAP算法无法解决的大数据集问题。
4 实验及结果分析
为验证FRSMEAP算法在大样本聚类问题上的有效性,本文将在不同的数据集上进行实验,除了FRSMEAP算法以外,也运行MEAP、AP、Kcenters[15]以及模糊C均值(fuzzy C-means,FCM)聚类算法[16]。用NMI(normalized mutual information)[17]、PR(Purity)[17]、RI(RandIndex)[17]、ACC(Accuracy)[17]作为聚类结果的评价指标。
实验中,FCM算法采用Matlab工具箱中自带的fcm函数,取默认参数设置。Kcenters、AP及MEAP算法中最大迭代次数为1 000,连续迭代100次直到聚类中心不变即停止计算。AP和MEAP算法的阻尼系数λ=0.9,逼近参数ε取值1E-5,η为3,核带宽h取值为0.4~0.8。每个算法执行20次,得到聚类评价指标的均值和标准差。
4.1JAFFE数据集
JAFFE数据集总共有213张图片,包含了10名女性的多种表情,每种表情有3~4张图片。
各个算法的聚类性能比较如表1所示。

Table 1 Average values and standard deviations of NMI and average computational time on JAFFE data set表1 在JAFFE数据集上NMI的均值和标准差以及聚类平均时间
表1表明,FCM是一种执行速度很快的聚类算法,但是它同Kcenters一样需要预先设定好聚类类别数,决定了这二者的不自适应性。在该数据集上FCM无法聚成10类,基本无效,印证了FCM适合凸数据集。MEAP能够正确将JAFFE聚成10类,比Kcenters、AP算法更适合处理此多代表点模型,但由于迭代过程繁重的时间开销,耗时最大。
4.2大规模人工数据集上的实验
人工数据集CreateArtData(CD)由两点簇和两个括弧形数据组成,总共有4类,如图1(a)所示。图1(b)表示FRSMEAP算法对压缩集的聚类结果。将人工数据样本大小从120递增到38 400时,4种聚类算法的聚类结果的4种评价指标如图2所示。
由图2(a)、(c)和(d)可知,在小样本情况下,FRSMEAP算法的NMI、RI和ACC指标不够稳定,仅低于FCM算法(k=4),却优于其他算法;当样本量分别大于600和1 920时,MEAP、AP和Kcenters算法已无法运行,而随着样本数的不断增大,FRSMEAP算法的各项聚类指标趋于稳定,并与FCM算法(k=4)相当,且保持了AP和MEAP的精度;与未知类别数的FCM算法(k=3)相比,FRSMEAP算法更具有优势。
表2给出了3种仿射类算法在样本数增加时运行时间的情况。当样本数多于1 920时,AP与MEAP算法在相同实验环境下均无法运行,而FRSMEAP算法仍能继续运行,且聚类时间虽然随样本数的增加而增加,但仍在可控范围内。图3描述了FRSMEAP算法的运行时间随样本数增加的线性渐近变化情况。
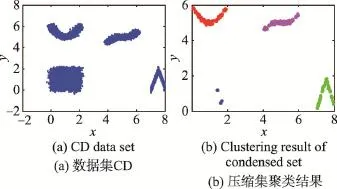
Fig.1 Synthetic data set and its condensed set clustering results图1 人工数据集CD与压缩集聚类结果
4.3真实数据集上的实验
考虑以下几个真实数据集Brain web、Sea、Shuttle和Iris,它们所含总样本数、每个样本的维数及所有样本的类别数如表3所示。
(1)Brain web(BW)数据集
由于MEAP算法很耗时,难以在相同实验环境下运行,故不取它作为对比算法。由图2(e)、(g)和(h)可知,在小样本容量情况下,FRSMEAP算法在4个指标上均能达到AP算法的效果。但当样本规模超过3 000时,AP算法已无法运行,而FRSMEAP算法的这4个指标和FCM算法(k=2)相当,并延续了AP与MEAP算法聚类效果良好的优点,与未知类别数的FCM算法(k=3)相比,FRSMEAP算法也有一定的优势。

Fig.2 Clustering evaluation index under different sample sizes of CD and BW data sets图2 CD和BW数据集不同样本容量下的聚类评价指标
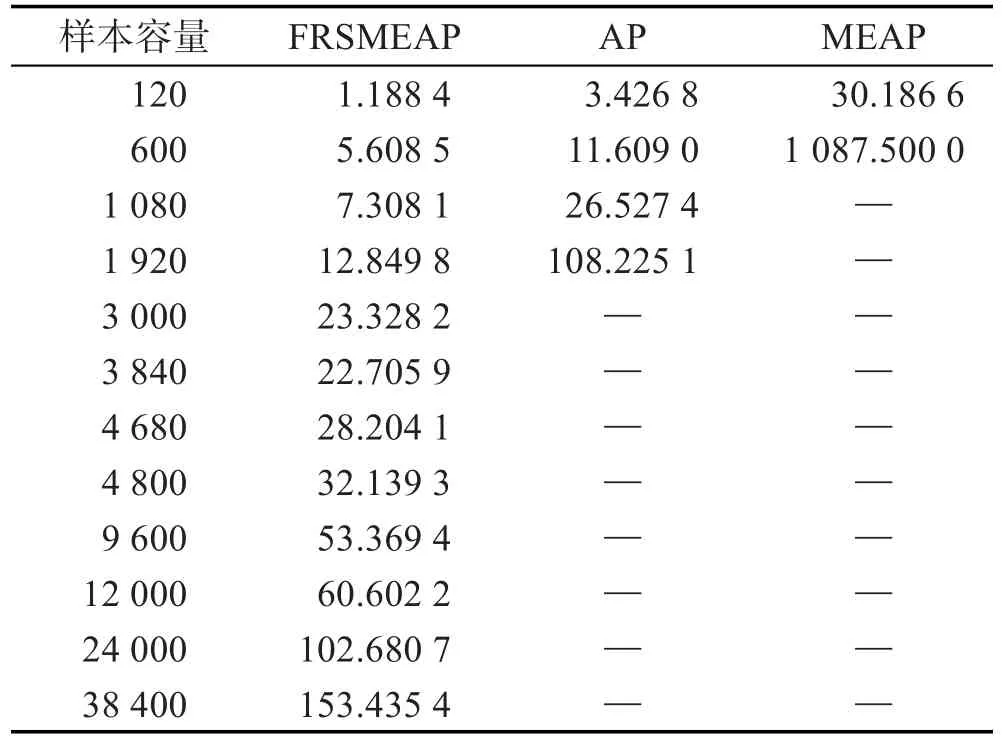
Table 2 CD sample size with clustering time表2 CD样本规模与聚类时间 s
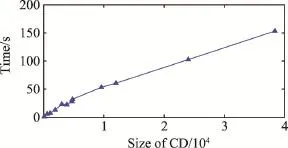
Fig.3 Changed time of the proposed algorithm under different sample size of CD图3 本文算法在不同CD样本规模下的时间变化
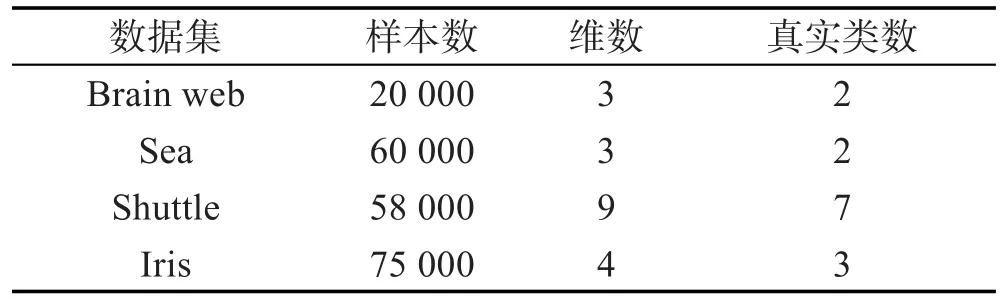
Table 3 Datasets description表3 数据集描述
当样本容量不同时,FRSMEAP与AP、MEAP算法的聚类时间如表4所示。

Table 4 BW sample size with clustering time表4 BW样本规模与聚类时间 s
由表4可知,在样本容量较小时,虽然AP算法也能够进行,但所需时间会随着样本容量的增加而快速增长;当样本数增大到一定量时,AP和MEAP算法均因内存溢出而无法执行,尤其是MEAP算法。而FRSMEAP算法在样本超过3 000时,执行效率明显优于AP、MEAP算法。图4亦给出了FRSMEAP算法运行时间随样本数增加的线性渐近变化情况。
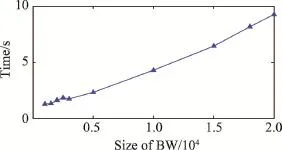
Fig.4 Changed time of the proposed algorithm under different sample size of BW图4 本文算法在不同BW样本规模下的运行时间
(2)Sea、Shuttle和Iris数据集
Iris来自UCI数据集,共3类,包含150个样本。为了验证大规模数据集下本文方法的性能,对Iris数据集进行扩充,扩充方法是为数据集样本的每一个分量增加一个均值为0,方差为1的正态分布偏移量,扩充后的Iris样本为75 000,如表3所示。由前面实验可知,AP、MEAP和Kcenters算法均无法处理大规模数据集,故以下在3个大数据集上利用FCM和 FRSMEAP算法进行聚类,以NMI、PR和ACC指标的平均值和标准差作为聚类结果,如表5所示,括号内的数值表示标准差。
由表5、表6和表7知,FRSMEAP算法在Sea数据集上的各项聚类指标均优于FCM算法,而在Shuttle数据集上虽然NMI指标略低于FCM(k=7)算法,但PR和ACC聚类指标均明显优于FCM算法。在Iris数据集上ACC指标要低于FCM(k=3)算法,但是要明显高于FCM(k=4)算法。
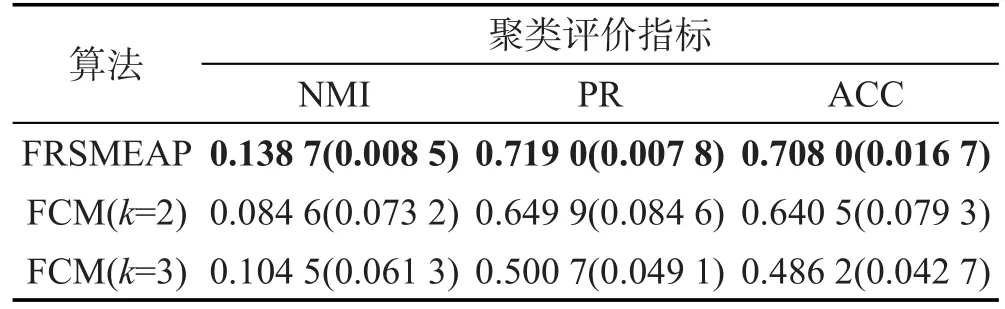
Table 5 Clustering results of two algorithms on Sea data set表5 两种算法在Sea大数据集上的聚类结果

Table 6 Clustering results of two algorithms on Shuttle data set表6 两种算法在Shuttle大数据集上的聚类结果

Table 7 Clustering results of two algorithms on Iris data set表7 两种算法在Iris大数据集上的聚类结果
综合而言,FCM算法总是非常快速,在真实数据集上的结果再一次表明它一般只适合凸形数据集,而且需要预先设定好类别数,无自适应性。由于FRSMEAP算法涉及CCMEB求解,所需时耗要大于FCM算法。因为压缩数据集保持了原数据属性,而且MEAP算法具有更好的决策边界,所以有很好的聚类效果,不低于FCM算法。因此,FRSMEAP聚类算法与传统的MEAP算法相比,不仅能够处理大数据问题,而且其聚类性能较优。
5 结束语
针对MEAP算法无法处理大数据集的问题,提出了一种快速多代表点仿射传播聚类算法FRSMEAP。该算法首先用FRSDE方法对数据集进行压缩预处理,并以压缩后的小样本数据集来模拟整个数据集,这样可大大减小MEAP算法的聚类时间。实验表明,FRSMEAP算法比MEAP和AP等算法更适合大数据聚类问题,而且其聚类精度不低于已有算法,表现出该算法的优越性。
References:
[1]Wang Zonghu.Research on the key techniques of clustering algorithm[D].Xi'an:Xi'an University of Electronic Science and Technology,2012.
[2]Frey B J,Dueck D.Clustering by passing messages between data points[J].Science,2007,315(5814):972-976.
[3]Wang Jun,Wang Shitong,Deng Zhaohong.Several problems in cluster analysis[J].Control and Decision,2012,27 (3):321-328.
[4]Dong Jun,Wang Suoping,Xiong Fanlun.Affinity propagation clustering based on variable similarity measure[J]. Journal of Electronics&Information Technology,2010,32 (3):509-514.
[5]Arzeno N M,Vikalo H.Semi-supervised affinity propagation with soft instance-level constraints[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2015,37 (5):1041-1052.
[6]Sun Leilei,Guo Chonghui.Incremental affinity propagation clustering based on message passing[J].IEEE Transactions on Knowledge&Data Engineering,2014,26(11):2731-2744.
[7]Du Yanxin,Ge Hongwei,Xiao Zhiyong.Affinity propagation image segmentation based on the fuzzy connection of degree method[J].Journal of Computer Applications,2014, 34(11):3309-3313.
[8]Wang Changdong,Lai Jianhuang,Suen C Y,et al.Multiexemplar affinity propagation[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2013,35(9):2223-2237.
[9]Zhu Manli,Martinez A M.Subclass discriminant analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2006,28(8):1274-1286.
[10]Dueck D.Affinity propagation:clustering data by passing messages[D].Toronto,Canada:University of Toronto,2009.
[11]Girolami M,He Chao.Probability density estimation from optimally condensed Data samples[J].IEEE Transactions on Pattern Analysis&Machine Intelligence,2003,25(10): 1253-1264.
[12]Deng Zhaohong,Chung Fulai,Wang Shitong.FRSDE:fast reduced set density estimator using minimal enclosing ball approximation[J].Pattern Recognition,2008,41(4):1363-1372.
[13]Tsang I W,Kwok J T Y,Zurada J M.Generalized core vector machines[J].IEEE Transactions on Neural Networks, 2006,17(5):1126-1140.
[14]Smola A J,Schökopf B.Sparse greedy matrix approximation for machine learning[C]//Proceedings of the 17th International Conference on Machine Learning,Stanford,USA, Jun 29-Jul 2,2000.San Francisco,USA:Morgan Kaufmann Publishers Inc,2000:911-918.
[15]Macqueen J.Some methods for classification and analysis of multivariate observations[C]//Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability,Statistics.Berkeley,USA:University of California Press,1967,1:281-297.
[16]Bezdek J C,Ehrlich R,Full W.FCM:the fuzzy C-means clustering algorithm[J].Computers&Geosciences,1984, 10(84):191-203.
[17]Liu Jun,Mohammed J,Carter J,et al.Distance-based clustering of GGH data[J].Bioinformatics,2006,22(16):1971-1978.
附中文参考文献:
[1]王纵虎.聚类分析优化关键技术研究[D].西安:西安电子科技大学,2012.
[3]王骏,王士同,邓赵红.聚类分析研究中的若干问题[J].控制与决策,2012,27(3):321-328.
[4]董俊,王锁萍,熊范纶.可变相似性度量的近邻传播聚类[J].电子与信息学报,2010,32(3):509-514.
[7]杜艳新,葛洪伟,肖志勇.基于模糊连接度的近邻传播聚类图像分割方法[J].计算机应用,2014,34(11):3309-3313.

LIU Ji was born in 1992.She is an M.S.candidate at School of Digital Media,Jiangnan University.Her research interests include pattern recognition and image processing,etc.
刘季(1992—),女,湖北鄂州人,江南大学数字媒体学院硕士研究生,主要研究领域为模式识别,图像处理等。

陈秀宏(1964—),男,江苏泰兴人,2000年于华东理工大学获得博士学位,2001年到2006年先后在南京大学和南京理工大学做博士后研究工作,现为江南大学数字媒体学院教授,主要研究领域为图像处理,模式识别等。

HANG Wenlong was born in 1988.He is a Ph.D.candidate at School of Digital Media,Jiangnan University.His research interests include pattern recognition and image processing,etc.
杭文龙(1988—),男,江苏南通人,江南大学数字媒体学院博士研究生,主要研究领域为模式识别,图像处理等。
Fast Multi-ExemplarAffinity PropagationAlgorithm for Large Data Sets*
LIU Ji+,CHEN Xiuhong,HANG Wenlong
School of Digital Media,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:liuji199209@163.com
The traditional affinity propagation(AP)is difficult to handle with multi-exemplar clustering,and has large space and time complexity,so it is not suitable for large data sets.To address these problems,this paper proposes a multi-exemplar affinity propagation using fast reduced set density estimator(FRSMEAP).At the beginning of clustering,fast reduced set density estimator(FRSDE)is introduced to preprocess large-scale data sets,and then the condensed set fully representing sample properties can be obtained.Multi-exemplar affinity propagation(MEAP)algorithm is used to cluster the condensed set,which can find better decision boundaries than AP.So the accuracy of clustering is improved.In order to get the final data partition,the K-nearest neighbor(KNN)is used to assign the remained data.The simulation results on synthetic and standard data sets show that the proposed algorithm can not only cluster on large-scale data sets,but also has the advantage of high precision and fast speed.
affinity propagation;clustering;large data sets;multi-exemplar
2015-05,Accepted 2015-07.
CHEN Xiuhong was born in 1964.He the Ph.D.degree from East China University of Science and Technology in 2000.From 2001 to 2006,he successively carries out post-doctoral studies at Nanjing University and Nanjing University of Technology.Now he is a professor at Jiangnan University.His research interests include image processing and pattern recognition,etc.
10.3778/j.issn.1673-9418.1505034
*The National Natural Science Foundation of China under Grant No.61373055(国家自然科学基金).
CNKI网络优先出版:2015-07-13,http://www.cnki.net/kcms/detail/11.5602.TP.20150713.1426.002.html
A
TP181

