基于BK树的扩展置信规则库结构优化框架*

苏　群，杨隆浩，傅仰耿+，余瑞银

1.福州大学 数学与计算机科学学院，福州 350116

2.福州大学 经济与管理学院，福州 350116

基于BK树的扩展置信规则库结构优化框架*

苏群1，杨隆浩2，傅仰耿1+，余瑞银1

1.福州大学 数学与计算机科学学院，福州 350116

2.福州大学 经济与管理学院，福州 350116

SU Qun,YANG Longhao,FU Yanggeng,et al.Structure optimization framework of extended belief rule base based on BK-tree.Journal of Frontiers of Computer Science and Technology,2016,10(2)：257-267.

针对扩展置信规则库（extended belief rule base,EBRB）系统在规则数较多时推理效率不理想的问题，引入BK树数据结构，提出了一种基于BK树的结构优化框架。首先根据置信规则在度量空间中彼此的距离建立EBRB的树形索引结构，然后通过设置阈值减少EBRB系统推理时搜索规则的数量，并激活关键规则，最终达到提高EBRB系统推理效率的目的。以非线性函数拟合、输油管道泄露仿真实验及分类数据集的对比实验，验证结构优化框架在EBRB系统中的有效性，实验结果表明，所提框架能够优化EBRB系统推理效率并提高决策准确性。

扩展置信规则库（EBRB）；证据推理（ER）；BK树；优化框架

1　引言

专家系统是人工智能领域最活跃和最广泛的应用领域之一，为了综合使用定量信息及由专家提供的不完整或不精确的主观信息，Yang等人在D-S证据理论[1-2]、决策理论[3]、模糊理论[4]和传统IF-THEN规则库[5]的基础上提出了基于证据推理算法的置信规则库推理方法[6]（belief rule base inference methodology using the evidential reasoning approach，RIMER）。相比于神经网络算法和支持向量机等“黑箱”方法，RIMER方法的推理过程具有更好的解释性和透明性[7]。

置信规则库（belief rule base,BRB）是RIMER方法中重要的组成部分，因此RIMER方法也称为BRB系统。为了提高BRB系统的推理能力，Yang等人[8]首次提出了BRB系统的参数优化模型，并通过Matlab优化工具箱中的FMINCON函数进行参数学习。随后，Chen等人[9]增加前提属性的参考值进行参数学习，提出了全局优化模型。Liu等人[10]提出BRB规则间的一致性问题，将BRB的一致性加入适应度函数，改进了目标函数。但上述方法均属于基于FMINCON函数的不断迭代的参数学习方法，导致算法效率不理想。针对该问题，基于群智能算法[11-12]的参数学习方法相继被提出，虽然算法效率有所提高，但是BRB的参数学习同样属于反复迭代的搜索过程。随后，Liu等人[13]将分布式置信框架引入置信规则的前件部分，并提出相应的扩展置信规则库（extended belief rule base,EBRB）系统表示、产生和推理的方法，该方法简单高效，且在EBRB系统无需进行参数学习的情况下，也具有良好的推理准确性。针对Liu等人的方法，其在推理效率方面仍存在瑕疵，主要体现在EBRB系统中规则均为无序存储状态，导致在对规则进行组合推理时需要遍历EBRB系统中所有规则以计算激活权重，当EBRB系统具有较多规则时，反复地遍历EBRB系统内规则将会导致推理效率低下，再加之当进行参数学习时需反复迭代，势必增加算法的时间开销，而这些都将制约EBRB系统的实现与应用。

BK树（Burkhard-Keller tree,BK-tree）通过对数据构建树形索引结构，进而可以对查询高效地搜索近邻数据[14]，BK树已经被广泛应用于模式识别、文本和多媒体信息检索中[15]。为了提高EBRB系统的推理效率以及组合更具代表性的规则进行推理决策，本文提出了一种基于BK树的结构优化框架。通过该结构优化框架可简单、高效地构建基于BK树的树形索引的EBRB系统，高效地搜索近邻规则以响应查询，进而克服传统EBRB系统在计算激活权重时需遍历整个EBRB的问题。结构优化框架的具体实现过程可概述为将EBRB内规则根据度量空间中彼此间的度量距离建立索引，在计算激活权重时利用索引对规则进行高效的搜索，再通过阈值设置的方式组合EBRB内关键规则，最终提升EBRB系统的推理效率和决策性能。此外，本文提出的基于BK树的结构优化框架有别于现有的参数学习方法，其并未改变EBRB系统的参数取值，因而可灵活地与任意EBRB系统或其他具备置信框架的系统及方法相结合，达到提升系统或方法效率的目的。最后引入函数拟合问题、输油管道泄漏问题和多个分类数据集，通过与传统BRB系统及传统EBRB系统在推理效率和决策准确性方面进行比较，说明本文所提结构优化框架是切实可行的。

2　扩展置信规则库系统

2.1扩展置信规则库的表示

为了表示数据或知识中存在的不确定性及不完整性，Yang等人基于传统IF-THEN规则，在规则的THEN部分引入分布式置信框架，并考虑前提属性权重和规则权重对推理结果的影响，提出了置信规则（belief rule）[6]。为了使规则表示信息时更加准确和全面，Liu等人在规则的IF部分也引入了分布式置信度框架，并提出了相适应的规则产生和推理方法[13]。表1对Yang和Liu提出的BRB系统进行了简单比较。

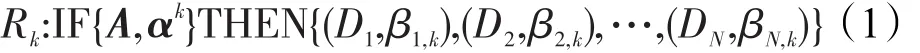
其中，(A,αk)是分布式置信度的形式，也可表示为，Ai,j表示第i个前提属性的第j个参考值，且参考值数量为Ji；T表示规则中前提属性的数量；L表示EBRB内规则的数量；N表示评价结果的数量；θk表示第k条规则的规则权重，反映第k条规则在EBRB中的重要度；δi表示规则中第i个前提属性的权重，反映规则中第i个前提属性相对于其他前提属性的重要度；βj,k(j=1,2,…,N,k=1,2,…,L)表示第k条规则中第 j个评价结果的置信度，如果，则称第k条规则是完整的，否则称第k条规则是不完整的。

2.2扩展置信规则库的构建

Liu等人提出了一种数据驱动的构建EBRB的方法。假设EBRB系统第i个输入数据xi为定量数据，且xi为数值形式。首先由专家或决策者建立参考值Ai,j(j=1,2,…,Ji)与数值量γi,j，并建立起对应关系，假设专家对参考值的偏好程度满足γi,j+1＞γi,j，那么输入xi可以等价地转换为分布式置信分布的期望形式：

其中αi,j的计算方法如下：

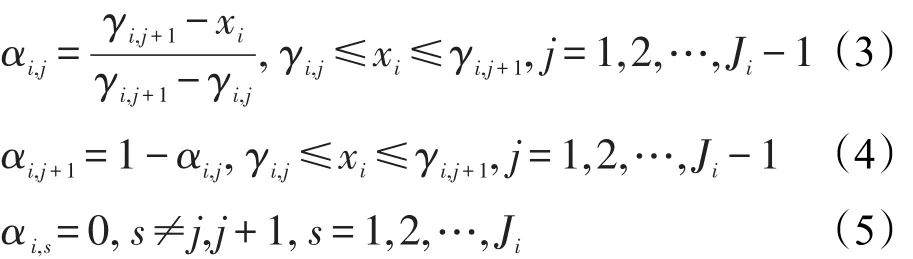
通过式（2）～（5）产生扩展置信规则的前件部分，与输入xi相对应的输出yi可采用同样的方法产生评价结果的分布式置信分布形式，从而由数据集构建完整的EBRB。

Table 1　Comparison between Yang-BRB system and Liu-EBRB system表1　Yang-BRB系统与Liu-EBRB系统的比较

2.3扩展置信规则库的推理

EBRB系统通过ER算法对规则进行组合，从而获得EBRB系统的推理结果。对于输入信息X，首先计算每条置信规则的激活权重，其中第k条置信规则的激活权重计算公式如下：

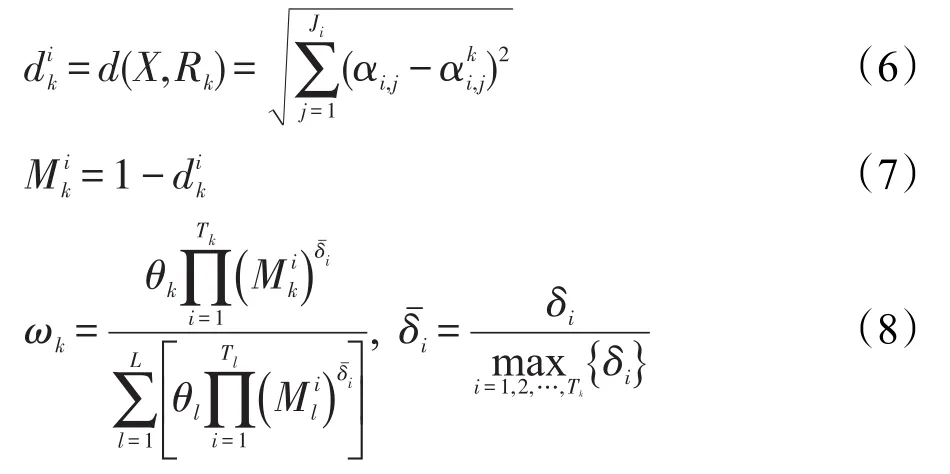
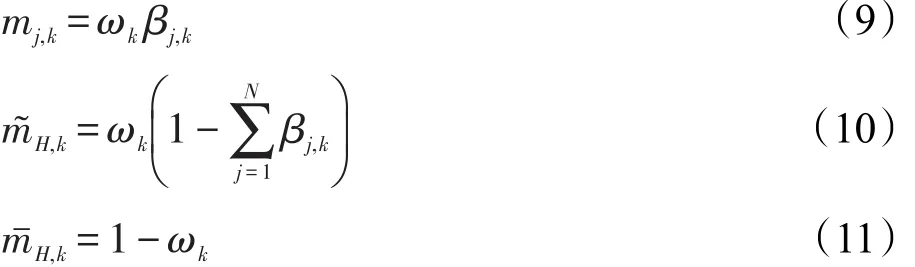
利用ER解析公式[16-17]，可求解激活规则组合后的对应评价结果Dj(j=1,2,…,N)的基本可信值，然后再转化为置信度的形式，具体公式如下：

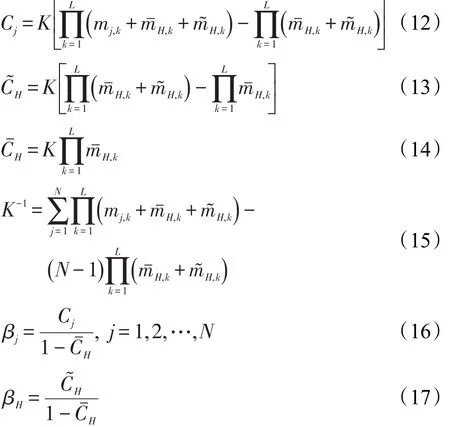
其中，βj表示评价结果Dj的置信度；βH表示未分配给任意评价结果的置信度。假设已知一组对应的输入输出(xm,ym)且m=1,2,…,T，根据评价结果分布式的置信度可以得到EBRB系统输出的期望效用值，方法如下：

3　EBRB的结构优化框架

EBRB方法能够简单高效地产生扩展置信规则，并避免了BRB系统存在的维数灾难问题[18]。但在EBRB根据输入进行推理时，扩展置信规则以无序的方式存储，因此需要依次遍历EBRB中的所有规则以计算规则的激活权重，当规则数量较大时会导致EBRB系统的推理效率不理想。为了解决这一问题，本文提出一个基于BK树数据结构的EBRB结构优化框架，并与数据驱动的EBRB方法[13]相结合，说明该框架的原理与作用。该结构优化框架首先计算置信规则间的度量距离，然后根据度量距离基于BK树将原先无序存储的规则建成树形结构的索引，在搜索激活规则时通过设置的阈值减少搜索规则的数量并得到关键规则，最后使EBRB系统在决策时具有良好的效率和准确性。

3.1Burkhard-Keller树

Burkhard-Keller树简称BK树，是由Burkhard和Keller提出的一种能高效地解决最优匹配问题的方法[14]。该方法对数据在一个度量空间中建立树形数据结构的索引，设X为所有可能取值的集合，d表示集合X的度量，∀x,y,z∈X，对于一个度量空间(X,d)，应具有以下3个性质。

（1）非负性：d(x,y)≥0，且d(x,y)=0当且仅当x=y。

（2）对称性：d(x,y)=d(y,x)。

（3）三角不等式：d(x,z)≤d(x,y)+d(y,z)。

BK树具有一个特点，即一棵子树中的所有节点与父节点具有相同的度量距离。图1展示了一个三层BK树的结构图，其中第一层节点为根节点；第二层有m+1个节点，表示可以将除根节点外的其他节点划分为m+1棵子树，第i(i=0,1,…,m)棵子树中的节点与根节点的度量距离都相同。要注意的是i并非一定等于度量距离，它可以是度量距离进行离散处理后对应的值。同样第三层子树中的节点与第二层的父节点也具有相同的度量距离。

基于度量空间的性质以及BK树的特点，文献[14]提出了一种有效的剪枝策略，可高效地实现多维空间中关键数据的搜索。需要注意的是，在常见的索引结构中，相似性查询有两种常用的方式，分别为K近邻查询和范围查询。对于一个询问q,q∈X，搜索BK树的索引得到的结果数据集Y应满足d(q,x)≤θd,∀x∈Y。这表明结果数据集元素与询问的度量距离满足阈值θd范围的数据，可认为是一种范围查询方式。

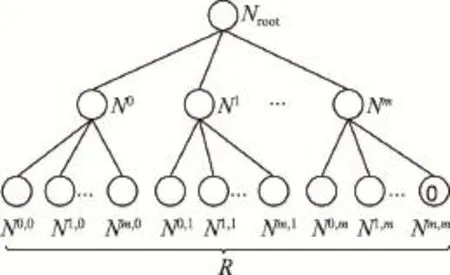
Fig.1　Three layer structure of BK-tree图1　三层BK树结构图

3.2基于BK树的扩展置信规则库构建

基于BK树构建EBRB是指基于BK树对扩展置信规则建立树形结构的索引。首先需要选择一个合适的度量空间对扩展置信规则进行度量。本文选择常见的欧氏距离作为度量距离并进行标准化，度量Rp和Rq两条规则的具体方法如下：

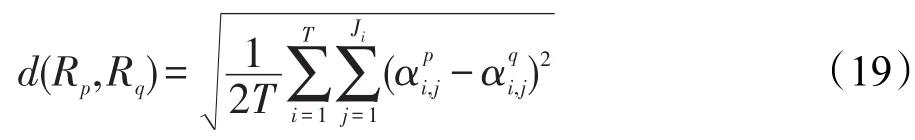
其中，扩展置信规则的前提属性均为分布式置信度的形式，第k条规则的第i个前提属性表示为。在对规则进行度量后即可建立基于BK树的扩展置信规则间的索引，具体步骤如下：

步骤2计算Rn和集合中剩余规则的度量距离，将剩余规则划分为m+1个子集合R0,R1,…,Rm，其中d(Rn,r)=i,∀r∈Ri，依次对每个子集合执行步骤3。

步骤3从集合Ri(i=0,1,…,m)中随意选择一条规则，建立其与Rn的索引并将其作为新的Rn。若子集合Ri的元素个数大于1，即，则执行步骤2，否则不做处理。

通过上述递归的算法步骤可以完成BK树的构建，从而将原本无序存储的扩展置信规则在一个度量空间中建立起树形结构的索引。假设现在有5条规则，规则只有1个前提属性，前提属性有两个参考值，度量距离为欧氏距离，5条规则在规则前件部分分别为：（0.4，0.6）、（0.5，0.5）、（0.3，0.7）、（0.2，0.8）和（0.6，0.4）。图2给出了对这5条规则建立BK树形索引的一种可能结构。

Fig.2　Index structure of 5 rules图2　5条规则索引结构图

3.3基于BK树的扩展置信规则库搜索

构建完基于BK树的EBRB后，接着介绍基于BK树的EBRB搜索策略。假设输入数据为X，则在基于BK树的EBRB中搜索满足d(Rn,X)≤θd的规则，并将其作为激活规则用于推理最终的决策结果，其中具体搜索步骤如下：

步骤1设置阈值θd，计算当前规则Rn和X的度量距离，令d=d(Rn,X)。若d≤θd则说明Rn可能被激活。

步骤2进行m+1次判断，m+1表示以当前节点为根的子树个数，若满足剪枝策略, k=0,1,…,m，则将第k棵子树的根节点规则作为新的Rn执行步骤3，否则不做处理。其中，dk表示Rn和第k棵子树中规则的度量距离。

步骤3计算当前规则Rn和X的度量距离更新d，若d≤θd，则说明Rn可能被激活，然后执行步骤2。

在对基于BK树的EBRB进行激活规则搜索时，利用“三角形不等式性质”可以得到步骤2中的剪枝策略。根据剪枝策略只搜索可能满足d≤θd条件的规则，减少了搜索规则的数量，从而提高EBRB系统推理的效率。以3.2节中的5条规则为例，现假设阈值θd=0.2，输入X为(0.45,0.55)。根据式（19）计算根节点规则和X的度量距离可得d=0.07，因此该规则可能被激活。然后根据剪枝策略可得左子树的结果为，而右子树的结果为，因此只对满足剪枝策略的左子树搜索而不对右子树搜索。随后计算节点(0.5,0.5)和X的度量距离可得d=0.07，因此该规则可能被激活，然后根据剪枝策略可得子树的结果为，从而不继续对子树中的规则进行搜索。

3.4结构优化框架下的规则推理

通过搜索得到可能被激活的规则集合后，需计算规则的激活权重。根据式（6）～（7）易知个体匹配度计算结果可能为负值，因此，本文提出改进的个体匹配度计算公式，改进后公式如下所示：

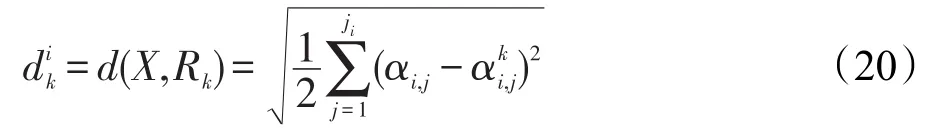
由式（2）～（5）可将定量输入值X转换为分布式形式，经式（20）可得输入值X与第k条规则的距离。此外，规则的不一致性极易影响EBRB系统的推理性能，由于在知识表示或获取时可能导致置信规则间存在不一致性，与此同时，当用历史数据产生置信规则时规则的不一致性还与噪声数据相关，因此规则推理时需采取适当的方法消除规则间的不一致性。本文采用文献[13]中的方法对规则的一致性问题进行处理。

由式（20）、（7）和（8）确定完激活规则后，根据ER方法对规则进行组合，得到评价结果的置信度分布情况，再计算效用值得到最后EBRB系统的推理结果。为方便叙述，下文将基于BK树的结构优化框架和EBRB系统相结合的系统称为BK-EBRB系统，其中BK-EBRB系统的流程如图3所示。

由图3可知结构优化框架是独立于EBRB系统的优化框架，其没有改变EBRB系统的参数值，可见基于BK树的结构优化框架易与其他具备信度框架的决策模型相结合。

表2对Liu-EBRB系统与BK-EBRB系统的复杂度进行比较。从表2中可以发现，BK-EBRB系统相比Liu-EBRB系统在构建系统时因为需要构建树形索引结构，所以复杂度更高，而当查询激活规则时BK-EBRB系统无需对规则遍历，可以高效地搜索近邻规则，相比Liu-EBRB系统具有更低的复杂度，当询问个数越多时，BK-EBRB系统的表现越好。

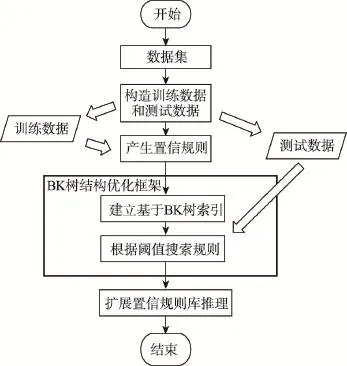
Fig.3　Flow chart of BK-EBRB system图3　BK-EBRB系统流程图

Table 2　Complexity comparison between Liu-EBRB system and BK-EBRB system表2　Liu-EBRB系统与BK-EBRB系统的复杂度比较

4　示例分析

为验证本文方法，引入非线性函数、输油管道泄漏两个实例以及多个分类数据集。实验环境为：Intel®CoreTMi5-4570 CPU@3.20 GHz；4 GB内存；Windows 8操作系统；算法实现平台Matlab R2012b与Visual Studio 2013。

4.1函数拟合问题

文献[13]证明了EBRB系统是通用逼近器，可以逼近任意非线性映射。本节将通过一个非线性数学函数来检验BK-EBRB系统的推理性能和效率，并与Yang的涉及局部参数学习的BRB系统[8]和Chen的涉及全局参数学习的BRB系统[9]进行比较。为方便叙述，以下分别简称为Yang-BRB系统和Chen-BRB系统。

非线性数学函数如下所示：

构建EBRB时，x为前提属性，并且具有7个参考值{0,0.5,1.0,1.5,2.0,2.5,3.0}，结果等级数目为5，相对应的等级效用值依次为{-2.5,-1.0,2.0,3.0}。在x的取值范围内均匀地选择500个数值，并根据式（21）得到对应函数的真实值，再根据前文所提方法构建BK-EBRB。其中阈值θd根据经验设定为0.01，测试数据为在x的取值范围内均匀选择的1 000组数据。

从图4中可以发现，Yang-BRB系统的模拟输出与数学函数的真实输出存在明显的差距，拟合效果并不理想；图5中Chen-BRB系统的模拟输出与数学函数的真实输出差距不大，仅在极大极小值处存在明显欠拟合问题，整体上具有较好的拟合效果；图6中BK-EBRB系统的模拟输出与数学函数的真实输出差距不大，能够很好地拟合该数学函数。

表3对3种方法测试结果及运行时间进行了比较。其中，Yang-BRB系统和Chen-BRB系统均运用Matlab工具箱中的FMINCON函数对BRB系统的参数进行学习，而BK-EBRB系统是将本文提出的BK树结构优化框架与数据驱动的EBRB方法相结合，并未进行参数学习。从表3中可以发现，BK-EBRB系统的模拟输出与真实值间的MSE为3种方法中最小的，在未进行参数学习情况下BK-EBRB系统也具有良好的推理能力。而参数学习是一个反复迭代的过程，需要大量的时间。因此，BK-EBRB系统的运行时间最短，与其他两种方法相比极大地提高了系统的效率。

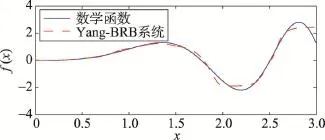
Fig.4　Function fitting chart of Yang-BRB system图4　Yang-BRB系统函数拟合图

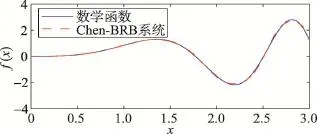
Fig.5　Function fitting chart of Chen-BRB system图5　Chen-BRB系统函数拟合图

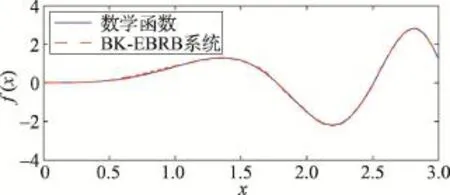
Fig.6　Function fitting chart of BK-EBRB system图6　BK-EBRB系统函数拟合图

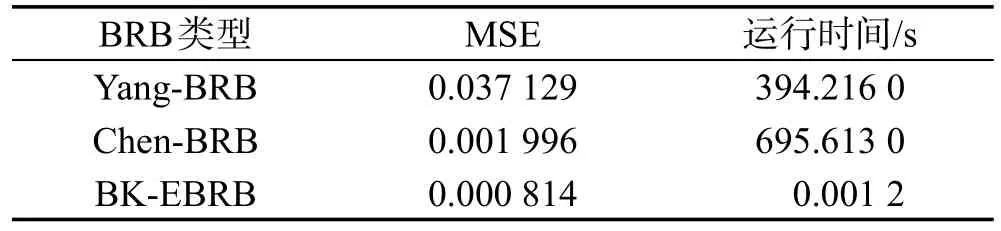
Table 3　Performance comparison of BRB system in function fitting表3　函数拟合BRB系统推理性能比较

4.2输油管道泄漏问题

以一个具体的实际问题——输油管道泄漏作为研究对象[9,19-21]，通过使用输油管道泄漏的真实泄漏数据对本文提出的BK-EBRB系统性能进行验证。在该实际问题中，当输油管道发生泄漏时，输油管道中油液的流量和压力会发生变化。因此，选择输油管道输入和输出的流量差（flow difference,FD）以及油液对管道产生的平均压力差（pressure difference,PD）对泄漏大小（leak size,LS）进行估计。

在构造EBRB时，选取了2 008组从无泄漏到发生25%泄漏状况的数据作为实验数据。因为FD和PD可以反映输油管道泄漏情况，所以系统的输入为FD和PD，而LZ则为输出。其中，根据专家经验得到前提属性FD有8个参考值，分别为{-10,-5,-3,-1, 0,1,2,3}；PD有7个参考值，分别为{-0.042,-0.025, -0.010,0,0.010,0.025,0.042}；输出LZ则有5个评价等级，分别为{0,2,4,6,8}。

在2 008组数据中，根据文献[9]的方法按照一定比例从3个时间段随机选择总共1 500条数据作为训练数据，产生置信规则，然后按照Liu的方法[13]和本文方法分别构造Liu-EBRB系统和BK-EBRB系统进行比较，并以平均绝对误差（mean absolute difference, MAE）作为评价指标。

图7和图8分别将Liu-EBRB系统和BK-EBRB系统（theta=0.4，theta即θd）产生的模拟输出与真实数据进行比较。两种方法均根据训练数据产生EBRB，后者引入基于BK树的优化框架。从图中可以发现BK-EBRB系统能较好地对输油管道泄漏情况进行检测，得到与真实值接近的结果。而当PD∈[-0.02,0]且FD∈[-10,-5]时，Liu-EBRB系统产生的模拟输出与真实值存在较大差距，BK-EBRB系统的模拟输出则更接近真实的情况。其主要是因为BKEBRB系统对置信规则建立基于BK树的索引，同时设置了阈值，进而减少了激活规则的数量。另一方面，由于仅对关键规则进行组合，减少了不一致规则对最终结果的影响，提高了系统的推理能力。

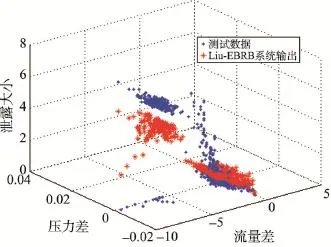
Fig.7　Liu-EBRB system output and test data图7　Liu-EBRB系统输出和测试数据

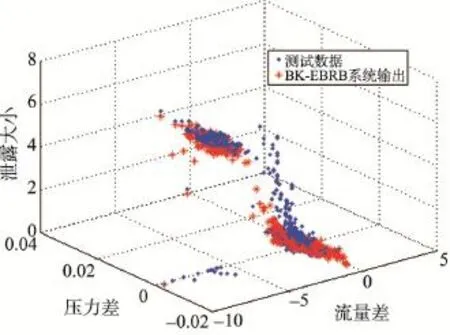
Fig.8　BK-EBRB system output and test data图8　BK-EBRB系统输出和测试数据

表4列出了Liu-EBRB系统和3个设置不同阈值的BK-EBRB系统产生的模拟输出与真实值间的MAE以及各自进行推理时搜索规则的次数。图9以柱状图的形式更形象地对4个EBRB系统在规则推理时的搜索规则次数进行比较。可以发现当BKEBRB系统的阈值设置为1.0时，BK-EBRB系统和Liu-EBRB系统具有相同的MAE并且搜索规则的次数一致。这是因为Liu-EBRB系统需要对置信规则进行完整的遍历，而当阈值为1.0时，剪枝策略没有发挥作用，BK-EBRB系统仍需遍历所有的规则。当BK-EBRB系统的阈值小于1.0时，搜索规则次数减少。因为当阈值小于1.0时，剪枝策略将发挥作用，可以缩小搜索规则的范围，减少搜索规则的数量，从而提高EBRB系统的推理效率。由表4还可以发现，相较于Liu-EBRB系统，BK-EBRB系统获得了更小的MAE，具有更好的推理能力。这是因为BK-EBRB系统通过阈值的设置，激活更为关键的规则进行组合，从而提升了EBRB系统的推理能力。

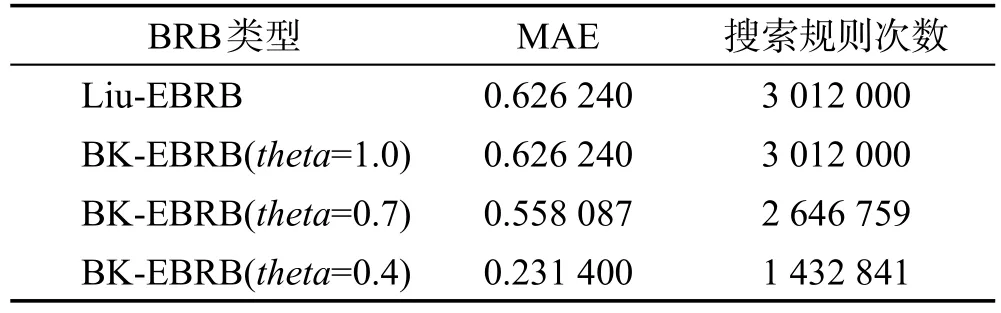
Table 4　Performance comparison of EBRB system in oil pipeline leak detection表4　输油管道泄漏检测EBRB系统推理性能比较

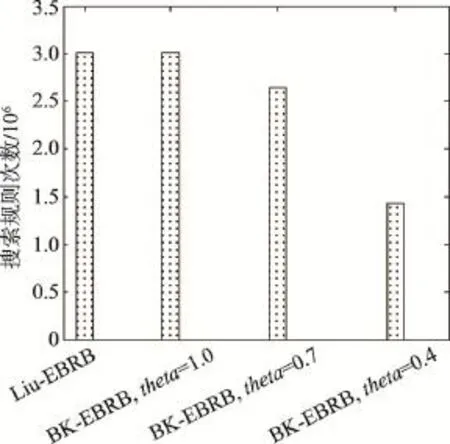
Fig.9　Search rules times in EBRB systems inference图9　EBRB系统进行推理搜索规则次数

通过输油管道泄漏实例对Liu-EBRB系统和BKEBRB系统进行比较，表明基于BK树的结构优化框架在提高EBRB系统推理效率的同时也可使EBRB系统能够更准确地反映系统的行为。

4.3分类数据集测试

为了验证本文方法的有效性，从UCI上选择了9个著名的分类数据集进行测试。通过5折交叉验证的方法，构造训练数据和测试数据。每个前提属性都根据数据范围设置6个均匀分布的参考值，评价结果数与分类数一致，以此根据数据产生扩展置信规则。然后根据本文方法构造4个BK-EBRB系统，并分别设置阈值theta为1.0，0.8，0.6和0.4，度量距离为欧氏距离，实验结果如表5所示。从表中可以发现，在大部分数据集上随着阈值的减小，BK-EBRB系统的推理准确性获得了提高，具有更好的分类准确度，这表明通过阈值设置激活关键规则可以提高系统的推理能力。BK-EBRB系统在Ecoli、Knowledge和Yeast这3个数据集上性能提升效果最为明显，而在Breast和Glass这两个数据集上，BK-EBRB系统的推理准确性呈现出先升高后降低的情况。阈值的设置会影响BK-EBRB系统的推理性能，合理的阈值将会使系统具有更好的推理性能，反之将会降低系统的推理性能。从表中可以发现，不同数据集相同阈值的推理能力不一致，应根据数据集的自身结构特点设置不同的阈值。阈值的设置可以通过枚举的方法对不同系统的推理性能进行比较，选择具有最优推理准确性系统对应的阈值，也可以将该问题视为一个最优化问题，并通过相关方法进行求解得到最优阈值。

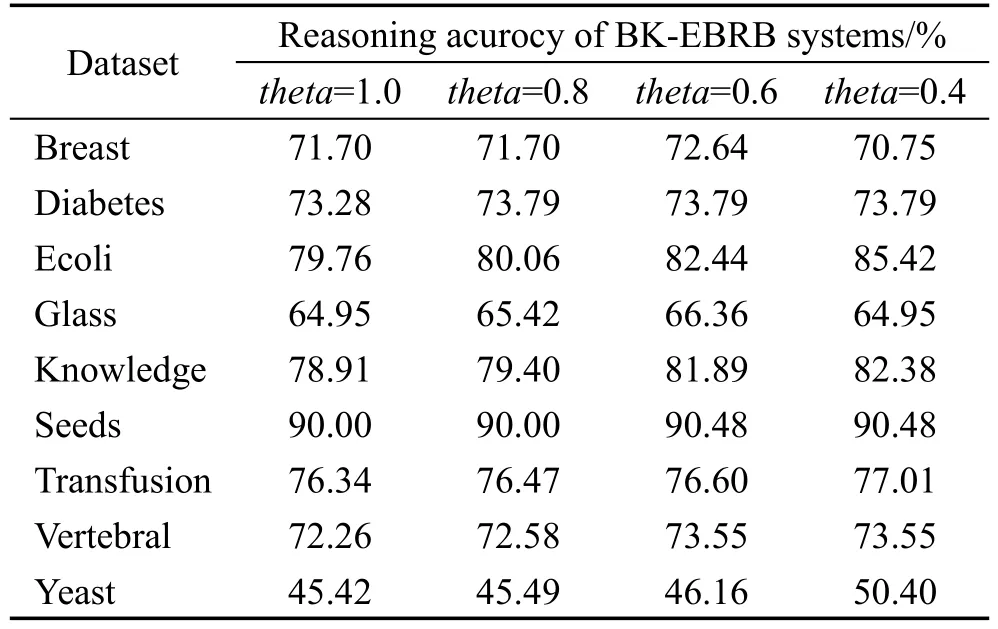
Table 5　Performance comparison of BK-EBRB systems on benchmarks表5　分类数据集上BK-EBRB系统推理性能比较

5　结束语

针对现有EBRB系统中因规则以无序的方式存储，导致在推理时需采用遍历EBRB内所有规则的方式计算激活权重，从而产生系统推理效率不理想的问题，本文提出了一种基于BK树的EBRB系统结构优化框架。

本文的优化框架通过对规则建立基于BK树的索引结构减少搜索EBRB中规则的数量；另一方面，通过设定合适的阈值筛选出更具有代表性的规则用于规则组合，提高EBRB系统的推理效率。此外，该结构优化框架还易与其他具有信度框架的决策模型相结合，具有良好的扩展性。示例分析中，通过在函数拟合问题和输油管道泄漏问题中与各类BRB/ EBRB系统进行对比，验证了本文方法能够提升EBRB系统的效率和决策性能；通过对多个分类数据集进行测试，进一步验证了方法有效性，并简单分析了阈值设置方法。在今后的研究工作中，将对合理设置阈值、激活置信规则及置信规则间一致性问题做进一步的研究，以期提出推理性能良好且更合理的BRB构建和推理方法。

References:

[1]Dempster A P.A generalization of Bayesian inference[J]. Journal of the Royal Statistical Society:Series B Methodological,1968,30(2):205-247.

[2]Shafer G.A mathematical theory of evidence[M].Princeton,USA:Princeton university press,1976.

[3]Wang C L,Yoon K S.Multiple attribute decision making[J].Berlin:Springer-Verlag,1981.

[4]Zadeh L A.Fuzzy sets[J].Information and Control,1965,8 (3):338-353.

[5]Sun R.Robust reasoning:integrating rule-based and similaritybased reasoning[J].Artificial Intelligence,1995,75(2):241-295.

[6]Yang Jianbo,Liu Jun,Wang Jin,et al.Belief rule-base inference methodology using the evidential reasoning approach-RIMER[J].IEEE Transactions on Systems,Man and Cybernetics:PartASystems and Humans,2006,36(2):266-285.

[7]Huysmans J,Dejaeger K,Mues C,et al.An empirical evaluation of the comprehensibility of decision table,tree and rule based predictive models[J].Decision Support Systems, 2011,51(1):141-154.

[8]Yang Jianbo,Liu Jun,Xu Dongling,et al.Optimization models for training belief-rule-based systems[J].IEEE Transactions on Systems,Man and Cybernetics:Part A Systems and Humans,2007,37(4):569-585.

[9]Chen Yuwang,Yang Jianbo,Xu Dongling,et al.Inference analysis and adaptive training for belief rule based systems[J]. Expert Systems with Applications,2011,38(10):12845-12860.

[10]Liu Jun,Martinez L,Ruan Da,et al.Optimization algorithm for learning consistent belief rule-base from examples[J]. Journal of Global Optimization,2011,51(2):255-270.

[11]Chang Leilei,Sun Jianbin,Jiang Jiang,et al.Parameter learning for the belief rule base system in the residual life probability prediction of metalized film capacitor[J].Knowledge-Based Systems,2015,73:69-80.

[12]Su Qun,Yang Longhao,Fu Yanggeng,et al.Parameter training approach based on variable particle swarm optimization for belief rule base[J].Journal of Computer Applications,2014, 34(8):2161-2165.

[13]Liu Jun,Martinez L,Calzada A,et al.A novel belief rule base representation,generation and its inference methodology[J].Knowledge-Based Systems,2013,53:129-141.

[14]Burkhard W A,Keller R M.Some approaches to best-match file searching[J].Communications of the ACM,1973,16(4): 230-236.

[15]Chávez E,Navarro G,Baeza-Yates R,et al.Searching in metric spaces[J].ACM Computing Surveys,2001,33(3):273-321.

[16]Yang Jianbo.Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties[J].European Journal of Operational Research, 2001,131(1):31-61.

[17]Yang Jianbo,Xu Dongling.On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty[J].IEEE Transactions on Systems,Man and Cybernetics:PartASystems and Humans,2002,32(3):289-304.

[18]Chen Yuwang,Yang Jianbo,Xu Dongling,et al.On the inference and approximation properties of belief rule based systems[J].Information Sciences,2013,234:121-135.

[19]Xu Dongling,Liu Jun,Yang Jianbo,et al.Inference and learning methodology of belief-rule-based expert system for pipeline leak detection[J].Expert Systems with Applications,2007,32(1):103-113.

[20]Zhou Zhijie,Hu Changhua,Yang Jianbo,et al.Online updating belief rule based system for pipeline leak detection under expert intervention[J].Expert Systems with Applications,2009,36(4):7700-7709.

[21]Zhou Zhijie,Yang Jianbo,Hu Changhua.Confidence expert system rule base and complex system modeling[M].Beijing:Science Press,2011.

附中文参考文献：

[12]苏群,杨隆浩,傅仰耿,等.基于变速粒子群优化的置信规则库参数训练方法[J].计算机应用,2014,34(8):2161-2165.

[21]周志杰,杨剑波,胡昌华.置信规则库专家系统与复杂系统建模[M].北京:科学出版社,2011.

SU Qun was born in 1991.He is an M.S.candidate at College of Mathematics and Computer Science,Fuzhou University.His research interests include intelligent decision-making technology and belief rule base inference,etc.

苏群（1991—），男，福建宁德人，福州大学数学与计算机科学学院硕士研究生，主要研究领域为智能决策技术，置信规则库推理等。

YANG Longhao was born in 1990.He is a Ph.D.candidate at College of Economics and Management,Fuzhou University.His research interests include intelligent decision-making technology and belief rule base inference,etc.

杨隆浩（1990—），男，福建南平人，福州大学经济与管理学院博士研究生，主要研究领域为智能决策技术，置信规则库推理等。

傅仰耿（1981—），男，福建泉州人，2013年于福州大学获得博士学位，现为福州大学数学与计算机科学学院讲师，CCF会员，主要研究领域为不确定多准则决策，置信规则库推理，移动互联网应用等。

YU Ruiyin was born in 1990.He is an M.S.candidate at College of Mathematics and Computer Science,Fuzhou University.His research interests include intelligent decision-making technology and belief rule base inference,etc.

余瑞银（1990—），男，福建福州人，福州大学数学与计算机科学学院硕士研究生，主要研究领域为智能决策技术，置信规则库推理等。

Structure Optimization Framework of Extended Belief Rule Base Based on BK-Tree*

SU Qun1,YANG Longhao2,FU Yanggeng1+,YU Ruiyin1
1.College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,China
2.College of Economics and Management,Fuzhou University,Fuzhou 350116,China
+Corresponding author:E-mail:ygfu@qq.com

To the problem of undesirable inference efficiency in extended belief rule base(EBRB)with large number of rules,this paper introduces BK-tree data structure and proposes a structure optimization framework based on BK-tree.Firstly,the index with tree structure of EBRB is made by the metric distance between the belief rules in the metric space.By setting the threshold,reducing the number of search rules and activating the key rules,the reasoning efficiency of the EBRB system is improved.Finally,simulation experiments on a nonlinear function,a practical pipeline leak detection problem and multiple classification data sets are conducted to validate the performance of the optimization framework combined with EBRB system.The experimental results show the proposed method can be used to optimize the reasoning efficiency and decision accuracy of the EBRB system.

extended belief rule base(EBRB);evidential reasoning(ER);BK-tree;optimization framework

2015-05,Accepted 2015-09.

FU Yanggeng was born in 1981.He the Ph.D.degree from Fuzhou University in 2013.Now he is a lecturer at College of Mathematics and Computer Science,Fuzhou University,and the member of CCF.His research interests include multi-criteria decision making under uncertainty,belief rule base inference and mobile Internet applications,etc.

10.3778/j.issn.1673-9418.1505065

*The National Natural Science Foundation of China under Grant Nos.61300026,71371053,71501047(国家自然科学基金);the Natural Science Foundation of Fujian Province under Grant No.2015J01248(福建省自然科学基金);the Science and Technology Project of Fujian Education Department under Grant No.JA13036(福建省教育厅科技项目);the Science and Technology Development Foundation of Fuzhou University under Grant No.2014-XQ-26(福州大学科技发展基金项目).

CNKI网络优先出版：2015-09-15,http://www.cnki.net/kcms/detail/11.5602.TP.20150915.1347.004.html

A

TP18；TP273.5