基于距离关联性动态模型的聚类改进算法*

陈雄韬，闫秋艳

中国矿业大学 计算机科学与技术学院，江苏 徐州 221116

基于距离关联性动态模型的聚类改进算法*

陈雄韬+，闫秋艳

中国矿业大学 计算机科学与技术学院，江苏 徐州 221116

CHEN Xiongtao,YAN Qiuyan.Clustering improved algorithm based on distance-relatedness dynamic model. Journal of Frontiers of Computer Science and Technology,2016,10(2):248-256.

针对大部分聚类算法无法高效地发现任意形状及不同密度的簇的问题，提出了一种高效的基于距离关联性动态模型的聚类改进算法。首先，为提高聚类效率，使用层次聚类算法对数据集进行初始聚类，并剔除样本点含量过低的簇；其次，为发现任意形状及不同密度的簇，以初始聚类结果的簇的质心作为代表点，利用距离关联性动态模型进行聚类，并利用层次聚类的树状结构进行有效的剪枝计算；最后，检验算法的有效性。实验采用Chameleon数据集进行测试，结果表明，该算法能够有效识别任意形状及不同密度的簇，且与同类算法相比，时间效率有显著的提高。

聚类；任意形状的簇；不同密度的簇；距离关联性；动态模型

1　引言

聚类是把无标签的对象划分到若干个簇中，使得同一个簇中的对象相似度最大化，同时不同簇中的对象相似度最小化[1]。聚类是一种重要的分析方法，被普遍地运用在数据挖掘、图像处理、统计学、生物学和机器学习等多个领域[2]。聚类算法通常可以分为5种类型：基于划分的方法、层次的方法、基于密度的方法、基于网格的方法和基于模型的方法。

基于划分的聚类算法，如k-means、k-medoid，CLARANS（clustering large applications based on randomized search）等，大部分是基于中心的划分方法，将样本点划分到与其最接近的簇中，这类方法只能检测到球形或圆形的簇。基于网格的聚类算法，如STING（statistical information grid）、CliQue（clustering in quest）、WaveCluster和DenClue（density-based clustering），其中WaveCluster和DenClue都能发现任意形状的簇，但它们使用的是静态模型，无法发现不同密度的簇。基于层次的聚类算法，如Birch[3]（balanced iterative reducing and clustering using hierarchies）、CURE（clustering using representatives）、Rock（robust clustering using links）、Chameleon[4]，其中只有Chameleon算法能发现任意形状和密度的簇[5]，但是Chameleon算法的时间复杂度为O(n2)。基于密度的聚类算法，如DBSCAN[6]（density-based spatial clustering of applications with noise）、VDBSCAN[7-8]（varied density based spatial clustering of applications with noise）和DVBSCAN[9]（density variation based spatial clustering of applications with noise）等，此类算法能够发现任意形状的簇且能够处理数据集中的异常值，因此在数据挖掘领域中被广泛使用[10-13]。其中DBSCAN是经典的基于密度的聚类算法，但因为它使用静态密度模型，所以只能处理用户指定密度的簇，且时间复杂度较高。VDBSCAN[7]算法能够检测不同密度的簇，能够根据k-dist（k-distance）自动选择一些输入的距离阈值参数（Eps）应对不同的密度。在文献[8]中VDBSCAN的参数k（k-dist）是基于数据集的特征自动生成的。然而VDBSCAN算法的时间复杂度与DBSCAN一样大。文献[9]提出了DVBSCAN算法，克服了DBSCAN不能处理局部密度变化的簇的问题，然而它的时间复杂度比DBSCAN还要高。

一个自然的簇应该可以是任意形状或密度的簇，因此不应该被局限于一个球形的算法假设，或者局限于用户指定的密度作为基于密度算法的需求。文献[5]提出了一种距离关联性动态模型，用以发现任意形状及任意密度的簇，聚类算法名为Mitosis，它利用样本点之间的距离关联性作为测量来区分不同密度的簇。因为Mitosis算法的处理对象为每一个样本点，所以时间复杂度有很大的改善空间。

Birch算法引入了聚类特征（clustering feature, CF）和聚类特征树（clustering feature tree,CF Tree）这两个概念，只需对数据集进行单次遍历就可以进行聚类，因此其时间复杂度较低，但是与传统基于划分的聚类算法一样，Birch算法只能发现球形的簇。

针对大部分聚类算法无法高效地发现任意形状及不同密度的簇的问题，本文将Birch算法与Mitosis算法的聚类思想结合起来，提出了一种两阶段聚类算法。利用Birch算法聚类速度快的特点，将其聚类的结果，以簇的质心作为代表点参与Mitosis的运算，有效降低了Mitosis算法的计算量，使得该方法能够发现任意形状及不同密度的簇，且时间复杂度得到了显著的改善。

2　基本概念

2.1Birch算法与Mitosis算法概述

Zhang等人[3]提出了Birch聚类算法，算法引入了两个概念：聚类特征和聚类特征树。聚类特征CF=(N,LS,SS)，其中N表示簇中样本点的数量，LS表示这N个样本点的线性和，SS表示这N个样本点的平方和，CF是对簇基本信息的概括，使得存储信息被高度压缩。聚类特征树是一个高度平衡的树，它含有两个参数，分别为分支因子B和阈值T，其中分支因子决定了每个非叶子节点最多拥有B个孩子，阈值T决定了每个簇的直径或半径不能大于T值。

算法的主要过程：利用树结构顺序处理每一个样本点，并把它划分到距离最接近的节点中，叶子节点存储聚类结果。

Yousri等人[5]提出了Mitosis算法，它能够发现任意形状以及不同密度的簇。文中提出了一种基于距离关联性的动态模型，用以发现自然形状的簇。距离关联性的概念反映的是基于距离的密度，即通过簇中样本点之间的平均距离来反映簇的密度，距离小则密度大，反之亦然。动态模型旨在维护每一个簇中样本点之间距离的一致性，因为同一个簇中每个样本点应该有一致的邻域距离来保持整个簇的密度一致，所以通过判断样本点之间是否满足这样的距离一致性，即可识别这些样本点是否属于同一个簇。该动态模型定义了一个距离关联性的聚类准则基于以下两点：（1）样本点的动态范围决定了这个样本点的密度环境（见定义3）。（2）定义了同一簇中样本点之间距离一致性的标准（见定义8）。

算法的主要过程：首先为每个样本点寻找其动态范围最近邻居，将每个样本点与其邻居建立关联，p1和 p2为关联的两个样本点，为它们之间的距离；将所有关联按其距离由小到大的顺序，依次处理这些关联的样本点；根据关联样本点之间的距离，以及关联的两个样本点所处的密度环境判断是否能将它们进行合并，最终得到聚类结果。算法包含两个参数f和k。f为影响每个样本点动态范围大小的自定义参数，k为影响距离一致性的自定义参数。

2.2相关概念

定义1质心：

其中，N为簇中样本点的数量；Xi为簇中的第i个样本点。

定义2半径：

当一个样本点被分到该簇时，计算该簇半径，当R＞T时，该簇将不接受此样本点。其中T为自定义的阈值。

定义3动态范围：

其中，P为样本点集；f≥1为用户自定义参数；d(p,q)为样本点p和q的距离。

定义4动态范围最近邻居：

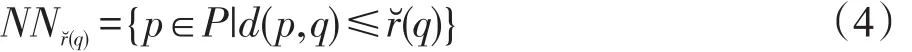
这样的动态范围邻域能够限制一个样本点与其邻居之间的最大距离，即只取距离该样本点不大于该上界值的邻居。

定义5局部平均距离：

用于检测一个样本点是否应该与另一个样本点或簇合并。

定义6簇的平均距离：

用于检测一个簇是否应该与另一个簇或样本点合并。其中Ac为簇c的关联集合，即在样本点合并为簇c的过程中所有满足合并条件（见定义8）的关联的集合。

定义7邻域平均距离：当样本点为独立样本点时，其邻域平均距离由式（5）计算，若样本点属于某个簇时，则其邻域平均距离由式（6）计算。

定义8合并条件：

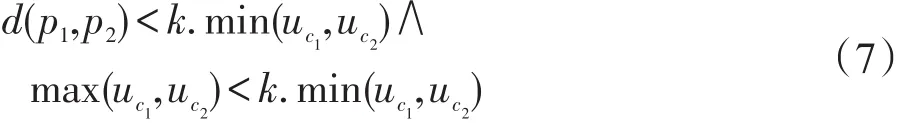
假设 p1和 p2为关联的样本点，其中 p1和 p2分别属于簇c1和c2，如果c1、c2满足式（7），那么它们将合并。其中分别为簇c1和c2的平均距离，由定义（6）计算，k≥1为用户自定义参数。开始时每个样本点自成一簇，如果簇只包含一个样本点，那么簇平均距离由式（5）计算。

3　本文算法

3.1算法思想

为了提高聚类算法的时间效率，本文旨在将数据集进行初始划分，形成多个大小近似的小簇，作为对原始数据的压缩表示，进而将充分接近的样本点作为一个整体处理，再依次将最接近的初始划分的小簇的密度是否近似作为判断依据进行合并，最终得到聚类结果。本文将结合Birch算法和Mitosis算法的优点提出一种高效的基于距离关联性动态模型的聚类算法BMitosis（Birch-Mitosis algorithm）。因为Birch算法为单次遍历数据聚类，具有算法时间效率高的特点，所以将Birch算法聚类结果作为对原始数据的压缩。而Mitosis算法提出了一种新颖的动态模型，具有发现任意形状及密度的特点，因此以Mitosis算法作为本文算法的第二阶段。

3.1.1算法的核心思想

假设符号x、y分别表示一个样本点，d(x,y)表示样本点x与y之间的距离，以元组(x,y,d(x,y))表示样本点x与y的关联。k≥1表示用户参数，u表示邻域平均距离。

图1说明了在聚类合并过程中满足式（7）的重要性。对于关联，在参考了两个样本点所处的邻域平均距离的情况下，它们之间的距离较小，满足条件，但是两个样本点的邻域平均距离相差较大，不满足。由图1可以看出 p1与 p2足够接近，但它们所处的邻域平均距离不近似，p2圆中方点的平均距离明显比p1圆中圆点的平均距离小。而对于关联，两个样本点的邻域平均距离相近似，满足，但它们之间的距离d(p3,p4)太大，不满足。由图1可以看出，p3圆中圆点的平均距离与p4圆中三角点的平均距离接近，但p3、p4之间的距离太大，明显大于它们的邻域平均距离。因此，在这两种情形中两个样本点都不能合并。

合并条件（式（7））同时考虑了两种情况：（1）两个关联的样本点是否接近，通过它们之间的距离与这两个样本点的邻域平均距离的对比来进行判断，若满足条件，则表示这两个样本点足够接近。（2）两个关联样本点的邻域平均距离是否近似，根据是否满足条件进行判断。这里的参数k决定了所能接受的近似程度。因此，算法在合并两个样本点为一个簇时，基于这样的思路：这两个样本点之间的距离应该是接近的，且它们所处的密度环境也是近似的。

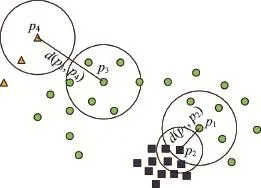
Fig.1　Importance of distance consistency图1　满足距离一致性的重要性

3.1.2算法的改进

（1）用Birch算法对数据集进行初始划分，剔除异常的簇，以每个簇的质心作为该簇内所有样本点的代表点，参与Mitosis算法的运算，以减少Mitosis算法的计算量，提高运算速度。

（2）在Birch算法的层次树状结构上提出剪枝策略，以降低为每个样本点求动态范围最近邻居的计算量。

（3）由于第一阶段以Birch初始划分得到的簇的质心作为该簇中所有样本点的代表点，为了兼顾这些簇中其他样本点分布的影响，将局部平均距离改为代表点局部平均距离，即将代表点到其动态范围最近邻居的平均距离改为代表点到其所代表的簇中所有样本点的平均距离。

在本文算法中，将式（5）改为：

其中，c(p)为代表点p所代表的簇；||c(p)为该簇中样本点的数量；x为c(p)中的所有样本点。而式（8）的值很容易在第一阶段的Birch算法中获得。在计算簇的平均距离时，关联集合将包括簇中所有代表点到其所代表簇中所有样本点的关联。

3.2算法步骤

BMitosis算法的整体步骤：

（1）Birch算法对数据集进行初始聚类，将聚类得到的小簇作为一个处理对象，为避免噪音数据的影响，将样本点数量小于阈值V的簇视为噪音数据，不参与第二阶段的聚类。将每个正常簇的质心作为该簇中所有样本点的代表点参与第二阶段的聚类运算。

（2）在层次结构上提出剪枝策略。第二阶段的运算需要为每个代表点计算其动态范围最近邻居，直接计算时间复杂度将是O(n2)，其中n为代表点的个数。因为层次聚类的结构中每一层簇为当前最相近簇的集合，所以在计算每个代表点的动态范围最近邻居时，先比较其所在簇的其他代表点，若当前层不能求得其动态范围内的所有最近邻居，则再往上一层继续查询，直到求得所有最近邻居为止。这样在为每个代表点求动态范围最近邻居时能有效缩小计算比较的范围，避免了相距甚远的代表点间的计算，有效降低了时间复杂度。

如图2所示：o1、o2、o3、o4、o5、o6分别为各自簇的代表点，O为它们上一层簇的质心。R为该层簇中O到其包含的所有代表点中距离最远的距离，由图可见R=d(O,o1)。d1为o3到该层簇中其他代表点的最近距离，则r1为o3的动态范围；d2为o2到该层簇中其他代表点的最近距离，则r2为o2的动态范围，如式（3）。d(O,o2)、d(O,o3)分别为质心O到代表点o2、o3的距离。当d(O,o3)+r1≤R时，如右虚线圆所示，则求o3的动态范围最近邻居，只需比较该层簇的所有其他代表点。当d(O,o2)+r2＞R时，如左虚线圆所示，则求o2的动态范围最近邻居，需要继续往上一层更大的簇中比较其他代表点。

（3）将代表点作为改进后Mitosis的数据集，将聚类结果中原始样本点数量小于总样本点数量1%的簇视为异常簇，将异常簇中的代表点划分到其最近的正常簇中。

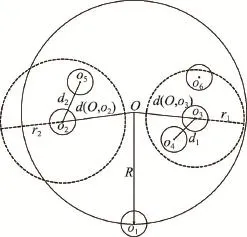
Fig.2　Pruning strategy图2　剪枝策略图示

3.3算法伪代码

4　实验及分析

实验由Windows 7操作系统，Intel®CoreTMi5-3470 CPU 3.20 GHz，4 GB内存作为实验环境。实验数据集采用Chameleon数据集[4]t5.8k、DS5和DS3，如图3所示。3个数据集均为8 000个二维数据点。t5.8k数据集包含6个不同大小、形状的簇，同时伴随随机噪音数据和一条直线痕迹贯彻这些簇。DS3数据集包含6个不同大小、形状的簇，同时伴随着随机噪音数据和特殊的痕迹贯彻这些簇。DS5数据集包含8个不同形状、大小、密度的簇，同时伴随着随机噪音数据，该数据集的难点在于它的每个簇彼此都很接近，且它们为不同的密度。

本文算法涉及5个用户自定义参数B、T、V、f、k。其中B为分支因子，T为聚类阈值，V为噪音阈值，f为动态范围参数，k为合并条件参数。在对以上3个数据集的聚类过程中，本文算法取值B=5，V=10，即在初始聚类时将小簇中样本点数量小于10的簇视为噪音数据。

Fig.3　View of datasets图3　数据集视图

4.1时间效率对比

图4显示了使用剪枝策略前后的时间效率对比。从图中可以看出当DS3数据集大于2 000时使用剪枝策略的时间消耗更低，而数据集小于2 000时使用剪枝策略的时间消耗略高。原因在于数据对象个数小于2 000时，由于代表点的数量较少，使用剪枝算法增加了额外的计算开销。而对数据集t5.8k与DS5的聚类过程，使用剪枝策略的算法运行时间始终比未使用剪枝策略低。这是由于不同的数据集有不同的数据分布情况，即使数据量一样，产生代表点的数量及分布情况也不一样。3个数据集的整体走势说明对大数据集聚类时使用剪枝策略能有效降低运行时间。

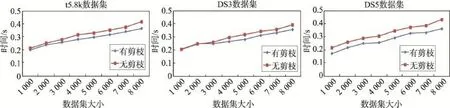
Fig.4　Time efficiency of pruning strategy图4　剪枝策略的时间效率

图5显示了本文算法的两个阶段的运行时间对比。第一阶段使用Birch算法，Birch算法为单遍扫描，因此时间整体呈线性增长。第二阶段在第一阶段基础上进行Mitosis算法，因此消耗时间均比Birch高。但因为第二阶段的处理对象为代表点，当数据集规模增加时代表点增加的速度较样本点慢，所以随着数据集规模的增加出现了算法运行时间增幅减缓的趋势，如DS3数据集大小从2 000到3 000的过程及DS5数据集大小从3 000到4 000及6 000到7 000的过程中，运行时间出现了平缓增加的现象。

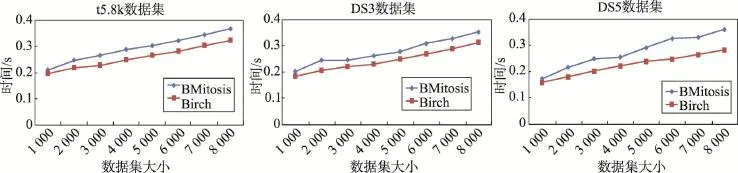
Fig.5　Comparison of time spending in two stages of BMitosis图5　本文算法两个阶段的时间效率

Fig.6　Time efficiency of BMitosis compared to other algorithms图6　本文算法与同类算法的时间效率对比

图6显示了本文算法与其他聚类算法的时间效率比较。因为Mitosis算法处理对象为单个样本点，需要对每个关联是否能够合并进行判断，所以算法运行时间随着数据集的大小波动较大。而本文算法以代表点作为处理对象，代表点的数量将远小于样本点，且当样本点数量增加时，样本点相距较近时可能被分在同一个簇中，因此代表点的数量不会直线增加，使得算法处理对象数量将大大降低。图中3个数据集本文算法运算时间均不足1 s。

4.2准确性对比

图3为数据集原图，图7为本文算法的聚类结果，聚类得到的簇以不同的颜色表示。从图7中可以清晰地看到不同的形状，且排除了大部分的噪音数据。对数据集t5.8k聚类算法参数为T=6.75，f=2.5，k= 3.0。对数据集DS3聚类算法参数为T=11.95，f= 2.6，k=2.7。对数据集DS5聚类算法参数为T= 14.25，f=1.3，k=3.24。

因为Mitosis算法以单个样本点为处理对象，所以容易对周围的噪音数据进行聚类，不能有效地排除噪音数据。图8为Mitosis算法对数据集t5.8k的聚类结果，算法参数为 f=2.3，k=2.65，数据集t5.8k含有很多的噪音数据，因此Mitosis算法在聚类6个正确的簇的同时，也对周边的噪音数据进行了聚类，没有很好地排除噪音数据。DBSCAN算法能够很有效地屏蔽噪音数据的干扰，但它只能发现静态密度的簇，当数据集中存在不同密度的簇时，算法不能有效地区分。图9为DBSCAN算法对数据集DS5的聚类结果，算法参数为Eps=10，Minpts=4，由于数据集DS5包含不同密度的簇，DBSCAN算法只能聚出6个簇。

Fig.7　Result of BMitosis图7　本文算法聚类结果

Fig.8　Clustering result of Mitosis图8　Mitosis的聚类结果

Fig.9　Clustering result of DBSCAN图9　DBSCAN的聚类结果

为比较算法的准确性，本文采用F-Measure[14]进行评估，计算公式为：

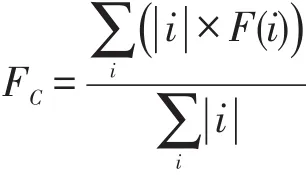
其中，|i| 为类i的样本点数量。

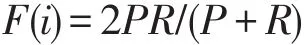
其中，Nij为同时在类i和簇 j的样本点数量；Nj为簇j中样本点的数量；Ni为类i的样本点数量。

从表1中可以看出本文算法的准确性介于两个算法之间，而DBSCAN算法在处理单一密度的数据集时有很高的准确性，然而在处理存在不同密度的数据集时准确性较差。

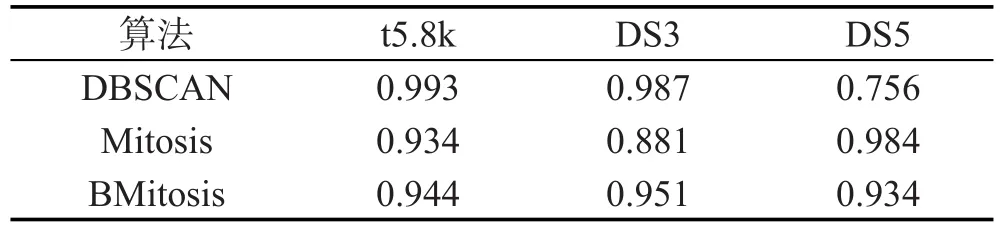
Table 1　Evaluation result of F-Measure表1　F-Measure评估结果

4　结束语

针对大部分聚类算法无法高效发现任意形状及不同密度的簇的问题，本文提出了一种高效的聚类改进算法BMitosis。该方法主要分为两个阶段：第一阶段用Birch算法对数据集进行初始聚类，并排除样本点数量小于阈值的簇，避免噪音数据的影响，以簇的质心作为整个簇的代表点参与第二阶段的聚类。第二阶段在层次结构上提出剪枝策略，降低计算每个代表点动态最近邻居的时间复杂度，再进行改进的Mitosis算法运算。实验表明BMitosis算法能有效排除噪音数据的影响，且能有效发现任意形状及不同密度的簇，在准确性较好的情况下，时间效率得到了显著的提高。当然本文算法引入的参数较多，减少算法对参数的依赖性是进一步需要解决的重要问题。

References:

[1]Mai S T,He Xiao,Feng Jing,et al.Anytime density-based clustering of complex data[J].Knowledge and Information Systems,2015,45(2):319-355.

[2]He Jinyuan,Zhao Gansen,Zhang Haolan,et al.An effective clustering algorithm for auto-detecting well-separated clusters[C]//Proceedings of the 2014 IEEE International Conference on Data Mining Workshop,Shenzhen,China, Dec 14,2014.Piscataway,USA:IEEE,2014:867-874.

[3]Zhang Tian,Ramakrishnan R,Livny M.BIRCH:an efficient data clustering method for very large databases[C]// Proceedings of the 1996 ACM SIGMOD International Conference on Management of Data,Montreal,Canada,Jun 1996.New York,USA:ACM,1996:103-114.

[4]Karypis G,Han E H,Kumar V.Chameleon:hierarchical clustering using dynamic modeling[J].Computer,1999,32 (8):68-75.

[5]Yousri N A,Kamel M S,Ismail M A.A distance-relatedness dynamic model for clustering high dimensional data of arbitrary shapes and densities[J].Pattern Recognition,2009,42 (7):1193-1209.

[6]Ester M,Kriegel H P,Sander J,et al.A density-based algorithm for discovering clusters in large spatial databases with noise[C]//Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining,1996:226-231. [7]Liu Peng,Zhou Dong,Wu Naijun.VDBSCAN:varied density based spatial clustering of applications with noise[C]// Proceedings of the 2007 International Conference on Ser-vice Systems and Service Management,Chengdu,China, Jun 9-11,2007.Piscataway,USA:IEEE,2007:1-4.

[8]Chowdhury A K M R,Mollah M E,Rahman M A.An efficient method for subjectively choosing parameter‘k’automatically in VDBSCAN(varied density based spatial clustering of applications with noise)algorithm[C]//Proceedings of the 2nd International Conference on Computer and Automation Engineering,Singapore,Feb 26-28,2010.Piscataway,USA:IEEE,2010:38-41.

[9]Ram A,Jalal S,Jalal A S,et al.A density based algorithm for discovering density varied clusters in large spatial databases[J].International Journal of Computer Applications, 2010,3(6):1-4.

[10]Kriegel H P,Kröger P,Sander J,et al.Density based clustering[J].Wiley Interdisciplinary Reviews:Data Mining and Knowledge Discovery,2011,1(3):231-240.

[11]Rinaldo A,Wasserman L.Generalized density clustering[J]. TheAnnals of Statistics,2010,38(5):2678-2722.

[12]Encyclopedia of machine learning[M].[S.l.]:Springer Science&Business Media,2011.

[13]Nanda S J,Panda G.A survey on nature inspired metaheuristic algorithms for partitional clustering[J].Swarm and Evolutionary Computation,2014,16:1-18.

[14]Hammouda K M,Kamel M S.Phrase-based document similarity based on an index graph model[C]//Proceedings of the 2002 IEEE International Conference on Data Mining, Washington,USA,2002.Piscataway,USA:IEEE,2002: 203-210.

CHEN Xiongtao was born in 1989.He is an M.S.candidate at School of Computer Science and Technology,China University of Mining and Technology.His research interests include data mining technology and pattern recognition,etc.

陈雄韬（1989—），男，福建政和人，中国矿业大学计算机科学与技术学院硕士研究生，主要研究领域为数据挖掘，模式识别等。

闫秋艳（1978—），女，江苏徐州人，2010年于中国矿业大学获得博士学位，现为中国矿业大学计算机科学与技术学院副教授，主要研究领域为时间序列挖掘，流数据挖掘等。

Clustering ImprovedAlgorithm Based on Distance-Relatedness Dynamic Model*

CHEN Xiongtao+,YAN Qiuyan
School of Computer Science and Technology,China University of Mining and Technology,Xuzhou,Jiangsu 221116, China
+Corresponding author:E-mail:chenxiongtao1989@163.com

In view of the fact that most of clustering algorithms fail to find arbitrary shaped and different density clusters efficiently,this paper proposes an efficient clustering improved algorithm based on distance-relatedness dynamic model.Firstly,in order to improve the efficiency of clustering,using hierarchical clustering algorithms for the data set to get the initial clusters and remove abnormal clusters.Secondly,in order to obtain arbitrary shaped clusters,taking the centroid of initial clusters as the representative point of all points in it,then running the distancerelatedness dynamic model for clustering,and using the tree structure of hierarchical clustering for pruning.Finally, verifying the effectiveness of the proposed algorithm.The algorithm is tested on the Chameleon dataset,the experimental results show that the algorithm can obtain arbitrary shape and different density clusters,and compared with the same algorithms,the time efficiency is improved significantly.

clustering;arbitrary shaped clusters;different density clusters;distance-relatedness;dynamic model

2015-06,Accepted 2015-08.

YAN Qiuyan was born in 1978.She the Ph.D.degree from China University of Mining and Technology in 2010.Now she is an associate professor at School of Computer Science and Technology,China University of Mining and Technology.Her research interests include time series mining and stream data mining,etc.

10.3778/j.issn.1673-9418.1507069

*The Natural Science Foundation of Jiangsu Province under Grant No.BK20140192(江苏省自然科学基金);the Youth Science Foundation of China University of Mining and Technology under Grant No.2013QNB16(中国矿业大学青年科技基金项目).

CNKI网络优先出版：2015-08-12,http://www.cnki.net/kcms/detail/11.5602.TP.20150812.1632.005.html

A

TP301.6