无图考题形助数，变式打磨获顿悟——以江苏如皋模考卷第28题为例

☉江苏省启东市百杏中学　沈颖生

无图考题形助数，变式打磨获顿悟——以江苏如皋模考卷第28题为例

☉江苏省启东市百杏中学沈颖生

一、写在前面

各地的中考、模考试卷中，全卷的最后一题必然考查数形结合、分类讨论两种思想方法，有些考题虽然没有出现图形（图像），但是解题时却需要心中有图、笔下构图，通过数形互助来思考.本文结合一道中考模考卷上的综合题，先给出思路突破，再就该题的解题教学给出相关思考，供研讨.

二、模考题的思路突破与解后反思

模考题（2016年4月江苏省如皋市中考模考卷，第28题）已知抛物线y=ax2-4ax+3和直线y=bx-4b+3相交于一定点A.

（1）求点A的坐标.

（2）设抛物线y=ax2-4ax+3与y轴的交点为B，直线y= bx-4b+3和直线OA分别与抛物线的对称轴相交于点C、D.问：是否存在一点C，使以A、C、D为顶点的三角形与△AOB相似？若存在，求出b的值；若不存在，说明理由.

（3）设抛物线y=ax2-4ax+3过点（2，-1），直线y=bx-4b+3与抛物线的另一个交点为P，若△POA的面积等于，求a和b的值.

思路突破：（1）题干很简洁，也没有函数图像，要想求出点A的坐标，需要反复读题，当解读出点A的多重价值后，才能破译第一问，这就是说点A是一个定点，不仅是抛物线与直线的交点.故将直线y=bx-4b+3变形为y= b（x-4）+3，这样容易发现当x=4时，函数值y=3，不再受到参数b的影响，即此直线必过点（4，3）.注意，还需要再验证该点是否一定在抛物线上，于是把x=4代入y=ax2-4ax+ 3，得y=3.定点（4，3）在抛物线y=ax2-4ax+3上，故点A的坐标为（4，3）.

（2）问题很抽象，没有图形，能确认点A、B的位置，于是可确认抛物线的对称轴为直线x=2，接下来构造草图分析，如图1，△AOB的形状是直角三角形，且三边也可很快得出，分别是3、4、5.如果要在对称轴上找一个符合要求的点C，则△ACD也应该是“3、4、5”式的直角三角形！

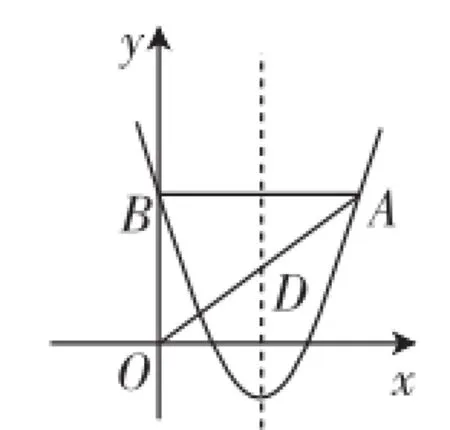
图1

图2

接着在图1中分析出两个可能的点C的位置，如图2，容易发现当点C1恰好是AB与抛物线对称轴的交点时，符合题意，这时直线y=bx-4b+3就是y=3，注意：不少学生可能会将这种情况舍去，因为这不是一次函数的图像了，出现这种错误的深层次原因是概念不清，对一次函数的图像与直线之间的从属关系没有辨析清楚.

图3

再考虑另一种情形，以点A为直角顶点时，会有点C2符合要求，当∠CAD=90°时，△CDA∽△AOB.结合直线OA的解析式为，根据互相垂直的两直线斜率乘积为-1，可得.综上，b=0或

（3）首先结合抛物线y= ax2-4ax+3过点（2，-1），可以确明a=1.这时就可画出抛物线的图像，如图3.

［解后反思］

1.解题关键在哪儿？

2.有什么经验值得积累？

对于无图题的思路突破，一般先要根据题意提供的条件信息解读出函数解析式，如果函数解析式不能顺利突破，则可借助已有定点、定值等信息锁定相关图形及位置，并缩小探究的范围，逐步显现问题的本质或结构.

三、复习导向之思

1.加强函数教学，关键是图像及性质

如人教社中数室资深编审章建跃博士所言，“函数是初中核心概念，在核心概念教学上要做到不惜时，不惜力”.函数教学的套路是概念、图像及其性质.同时要引导学生辨析函数与图像之间的从属关系，比如一次函数的图像是直线，但直线一定是一次函数吗？反比例函数的图像是曲线，但曲线一定是反比例函数吗？如果这些初始概念没有辨析清楚，则很容易出现上文模考题第二问中学生舍去b=0的那种情形.而对于二次函数来说，如果学生对像模考题第二问中A、B点同时在二次函数图像上有一定认识，则二次函数的对称轴就能得到确认，这些信息的确认时间将是优秀学生解答把关题的重要区分所在.

2.无图问题突破，重要的是构图训练

不少数学试卷的把关题都是无图题，本身就是考查学生根据文字信息、符号信息，结合对数学概念的理解和分析构图解题能力，有些学生习惯了图形辅导思考，自己结合题意画出图形分析能力偏弱.这说明在平时的解题教学过程中，要注重引导学生构图分析，这方面较为理想的载体是几何文字命题的证明与求解.就笔者教学实践经验所见，这个方向是目前教研的弱项，这可能不是一线教师的教研盲点所造成的，而是与世纪之初课改之后的各级教材的“引领”有关.比如对比上个世纪的数学教材，一个重要的不同就是大量文字命题退出教材，取而代之的是画好图形、图像，学生只要看图找条件就可进入解题流程，这种“去头、掐尾、烧中段”的教学取向使得学生的构图能力不断弱化.

四、命题商榷

命题如同教学，也是遗憾的艺术.考虑到模考题的第二、三问之间无甚关联，且所谓题干中的直线y=bx-4b+3在第一问已基本发挥了它的价值，后面第二、三问两问虽然也用到该直线的解析式，但只是简单的增加解题层次，没有真正体现该直线的价值.作为文末，本着命题兴趣，给出打磨变式，供研讨.

（模考题打磨变式）已知平面直角坐标系xOy中，抛物线l1：y=ax2-4ax+3与y轴的交点为A，直线l2：y=bx-4b+3经过一个定点B.记抛物线l1的对称轴为l3.

（1）求点B到直线l3的距离.

（2）若直线l3与直线OB交于C，分析直线l3上是否存在点D，使以B、C、D为顶点的三角形与△AOB相似？若存在，求出b的值；若不存在，说明理由.

（3）当抛物线l1的顶点E恰落在直线l2上，且△ABE的面积为时，求a和b的值.

【变式意图】原题干中的指出抛物线与直线交于一定点，属于重复，因为该抛物线的对称轴已明确，与y轴的交点也明确了，则交点与对称轴的对称点即为定点B，这些应该由考生独立探究得出；原模考题的第二、三问之间缺少必要的关联，打磨改编之后，第三问的就对应着第二问中的一个点D.而这些都需要经历解题探索“柳暗花明”后，获得“蓦然回首，那人却在灯火阑珊处”的顿悟.

1.罗增儒.数学解题学引论［M］.西安：陕西师范大学出版社，2008.

2.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

3.夏盛亮.引导回归教材，倡导开放教学——一次县级期末卷的命题取向分析［J］.中学数学（下），2014（1）.

4.鲍建生，顾泠沅，等.变式教学研究［J］.数学教学，2003（1，2，3）.Z