优化课堂提问，提高初中数学课堂效率

浙江省桐乡市南日初中 沈国英

优化课堂提问，提高初中数学课堂效率

浙江省桐乡市南日初中 沈国英

课堂提问是一门艺术，也是一种教学方法。通过优化课堂提问提高课堂效率是数学课堂成功的关键。本文结合自己的教学实践，从课堂提问方面着手：从问题的生成、问题的引入、问题的设计三个方面，探讨如何最大限度地优化课堂提问，提高课堂效率，使课堂提问成为启发以学为主课堂模式下学生善思善问的有效途径。

初中数学 课堂提问 问题设计

“课程标准”的教学策略强调教学过程是师生交往、持续发展的过程，强调构建充满生命的课堂教学体系。而数学是训练思维的学科，每节课堂都是在明确的学习目标下，从学生已有的知识生成新的问题，带着我要解决什么样的问题，需要具备什么样的知识，要掌握什么样的技能，通过什么样更好的方式解决这个问题。数学最后就是怎样解决问题的学科。要提高数学课堂的有效性，更好地解决新问题，需要化繁为简的处理教学中的疑难问题。要使难点不难，让学生更好地掌握，关键在于教师在课堂上对教材的处理。合理“提问”是构建有效课堂，促进师生、生生互动的催化剂。笔者认为，如果能将一堂数学课的难点内容浓缩为一个个精妙的问题，将这些问题环环相连作为化繁为简的点睛之笔，由点及面地展开教学，会使思维能力正处于发展期的初中生更好地生成新知，理解新知，运用新知，巧妙地将课堂串起来，进而轻松解决问题。

一、问题生成以学生为前提

学生是学习的主体，教学的出发点和归宿点都体现在学生身上，因此在数学课堂中问题的设计，应体现学生的主体性。分析教材的同时，着力分析学生的学习基础和能力，从学生的角度来定教，做到低起点，高效率。

案例：浙教版新教材七年级（上）“6.8余角和补角”中有个例题：

已知一个角的补角是这个角的余角的4倍，求这个角的度数。

这道题用直接列算式的方法比较困难，因此教材分析提示用设未知数列方程的方法解。利用代数方法解决几何问题，数量关系又有些纠结，对于初一的学生，像笔者所在的农村初中是有难度的，是本堂课的难点。

策略：学生解决不了这类问题的关键在于，一个角、这个角的余角、这个角的补角这三个概念的理解和数量关系的不明确。所以笔者采用了如下的方式进行处理：讲解例题之前先作了如下铺垫：

（1）∠1=30°，则∠1的余角=___°，∠1的补角=___°。（学生很容易解决了）

（2）∠1的余角=50°，则∠1=___°，∠1的补角=___°。

（3）∠1的补角=120°，则∠1=___°，∠1的余角=___°。

（4）∠1=x°，则∠1的余角=___°，∠1的补角=___°。（有上面的基础，学生也很容易解决了）

通过上面的一系列小问题的环环相扣，把难点降低，寻找解题的关键：一个角、这个角的余角、这个角的补角，这三个量中，只要已知一个量，其他两个量就可以求出来或表示出来，然后分别给定条件让学生来体会，加深对问题的理解，形成模式。

明确了这一点后，已知具体角度数据的可以直接利用数量关系求解，未知的可以用设未知数的方式来表示，只要抓住这个基本点，类似的求解题都有了方向。

二、问题引入要激发学生思维

数学教学是数学活动的教学，而思维活动是数学课堂教学中学生的主要活动。数学课堂教学的质量，关键是看学生的思维有没有被激活。产生有效思维，是整个课堂体系清楚明了，形成有效的解决问题的模式。课堂教学要使学生思维在原有的基础上获得尽可能好的发展，问题的设计也要能够激发学生对知识的深入开发的思维。

案例：浙教版八年级下册“多边形”内角和计算公式的运用中，经常出现这种题型：

（1）已知一个多边形的每个外角都为60°，这个多边形的内角和为______°。

（2）已知一个多边形的内角和为540°，这个多边形有______条对角线。

这类求解题，由于数量关系没有那么明确，公式运用不够熟练，学生解起来比较困难，需要教师引导，将问题细化，层层深入，步步逼近，以达到降低难度的目的。

问题1：引导学生将这几个量的公式写出来，比较一下；

问题2：公式中最重要的元素是什么，有什么启发；

n边形内角和公式：180（n-2）

n边形外角和：360°

小结：n边形内角和、n边形对角线的公式中，字母n表示的都是多边形的边数，这一元素将这几个公式串联起来。因此，多边形的内角和、多边形的对角线、多边形的边数，多边形的外角特征四个量中，已知其中一个便可求解其他各量，而其中的中介就是多边形的边数，只要根据已知，用公式先求出多边形的边数，再利用公式求其他量即可。

数学是要掌握知识技能并运用的学科，基本知识的识记不是难点。现在很多学生面临这样的学习问题：课堂上听听似乎都懂，在老师讲解下做题也不难，但自己遇到问题要灵活运用时却有很多困难。这说明，看似简单的知识，不深入理解，找到联系，是形成不了解题模式的。解题不仅是熟能生巧的结果，关键是理解各个知识的基本意义，思考其中关系，激发学生把数学知识串联并融会贯通的学习思维。

三、问题设计凸显数学本质

数学活动是学生经历数学化过程的活动，又是学生自己建构数学知识的活动。因此教师应该把自己对数学本质的理解作为教学设计的灵魂，将其自始至终贯串在数学课堂中。对课堂关键点的把握也要在自身数学修养上，为学生开辟了解数学本质的机会。

案例：浙教版八年级下册“多边形”中，教材中探索多边形的内角和利用了一份表格来完成探索，如下：

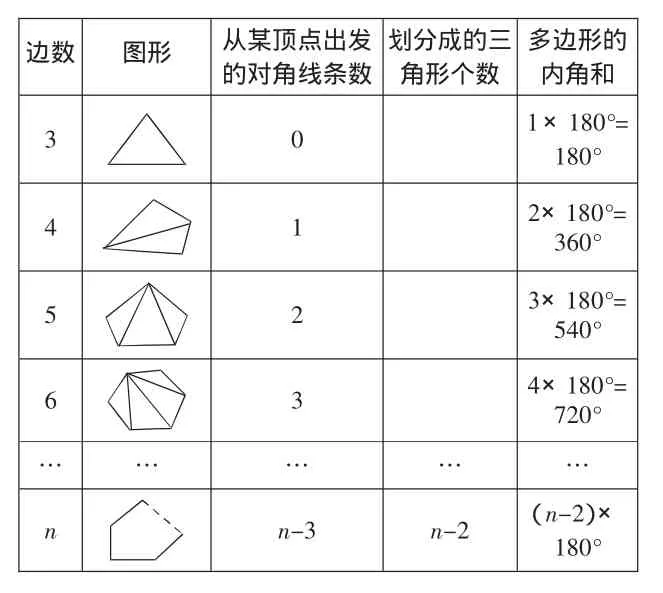
如果教师直接利用教材表格，由于学生有前面四边形内角和的知识铺垫，解决起来也没有什么问题。填完表格学生得出公式就可以应用解题了。但这种方式学生的参与受到了思维的限制，难以体现几何探索的本质。

问题设计：本节探索的本质即为多边形的问题需要转化的思想，既然上节课探索四边形时呈现了多种方法，在继续探索其他多边形时，只要提出一个问题：你是怎么解决四边形问题的？请类比！让学生充分参与，多角度展示，开出思维之花。体会多边形探索的本质——转化为三角形或四边形。（学生方法集锦如下）如此，也为本节例题（本节的例题是本节的难点，需要添加辅助线，转化为三角形）的解决提供了分析法。

方法1：把五边形分成三个三角形，3个180°的和是540°。

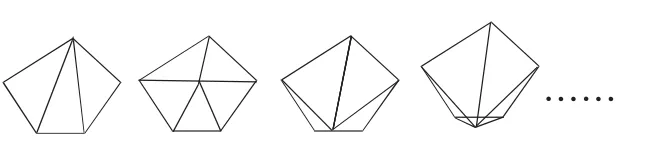
方法2：从五边形内部一点出发，把五边形分成五个三角形，然后用5个180°的和减去一个周角360°。结果得540°。

方法3：从五边形一边上任意一点出发把五边形分成四个三角形，然后用4个180°的和减去一个平角180°，结果得540°。

方法4：把五边形分成一个三角形和一个四边形，然后用180°加上360°，结果得540°。

当课堂上学生探索时，教师不要过多限制思维方式，而是精炼地提出思维的关键点，这样给学生留下了思维的时间和空间，并能更好地体会数学的本质。为解决类似的题目提供了方向。

问题可大可小，却要有所指向，值得我们关注和研究。精心设计每一个教学细节，就能激发学生的思维，培养学生精练的概括能力，化繁为简，提高课堂效率。

[1]中华人民共和国教育部.数学课程标准.北京师范大学出版社

[2]余文森.新课程的深化与反思.首都师范大学出版社

[3]朱士泉.关于课堂教学创新的思考.教育出版社