关于三角形的两个命题

内江师范学院数学与信息科学学院　王文强　陈明越

关于三角形的两个命题

内江师范学院数学与信息科学学院王文强陈明越

命题一：在一切同底且周长相等的锐角三角形中，等腰三角形的面积最大。

分析：当底相等，要使周长相等，则只需要不同的三角形两腰之和相等。由三角形的面积公式可知，同底的三角形，底对应的高越大三角形的面积越大。

证法1：如图△ABD和△ABE是同一圆的内接三角形，和为同底的等腰三角形，且AB//CD。

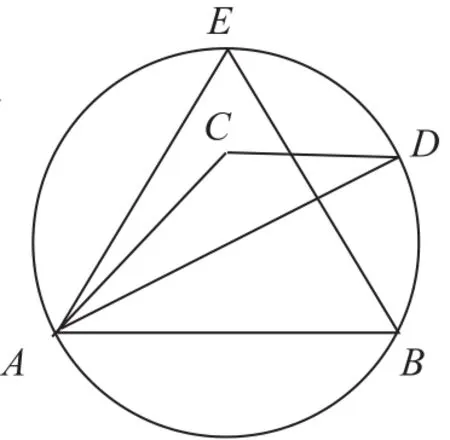
图1

应减小△ABD两腰的长度，则面积也相应减小，故命题一成立。

证法2：如图2，△ABC为等腰三角形，AB=AC且AC+AB=AD+BD，设AD为最长的一腰，构造△ABD的外接圆，则圆的直径2R≥AD＞AC∴C点在圆内。

图2

即S△ABC＞S△ABD，故命题一成立。

命题二：在一切同底且周长相等的三角形中，等腰三角形的面积最大。

分析：若不在锐角三角形中，正弦的图形可知不能通过角的大小判断正弦值的大小。先做出符合命题的图形3，△ABC是等腰三角形，AC+BC=AD+BD。

证法1：过C点做直线L平行AB，再做B点关于L轴的反射点E，并连接EC，ED和EB，因为∠ECL=∠BCL=∠CAB，

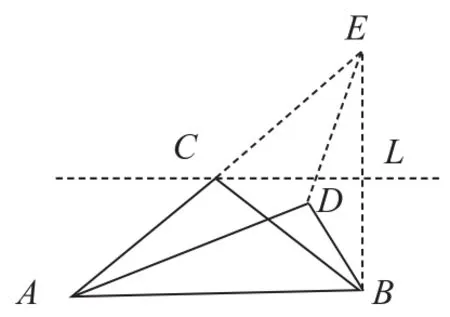
图3

证法3：设AC+BC=AD+BD=2a（2a为大于AB的定值），顶点D的运动轨迹为椭圆（不含端点）。

由椭圆的性质和图形可知，△ABC的高大于△ABD的高，∴S△ABC＞S△ABD。

将此命题用于生活中，满足相同条件的情况下，可用同样的材料得到最大的面积，达到降低成本的要求。

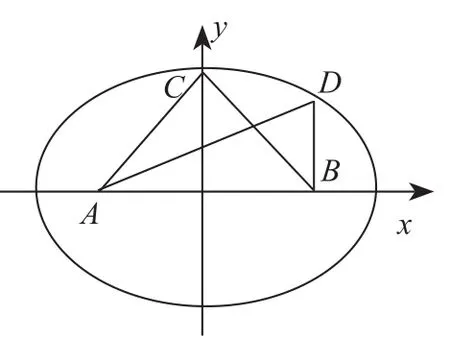
图4

［1］张雄，李得虎.数学方法论与解题研究［M］.北京：高等教育出版社，2013.

［2］张景中.会说话的图形［J］.数学教学通讯，2009（25）.

［3］张景中.把数学变得容易些［J］.河南教育，2000（10）.