一类新的q元量子MDS码

牛　刚，亓延峰

(杭州电子科技大学理学院，浙江 杭州 310018)



一类新的q元量子MDS码

牛刚，亓延峰

(杭州电子科技大学理学院，浙江 杭州 310018)

量子纠错码在量子信息处理和量子计算中有着重要的应用.q元量子MDS码是一类重要的最优量子纠错码，此类量子码的参数满足相应的量子Singleton界.构造q元量子MDS码具有重要的理论和应用意义.但构造码长q+1的q元量子MDS码是比较困难的，许多码长(q+1)(q-1)/m的q元量子MDS码,其中m整除q+1或q-1,已经被构造出来.在HE Xiangming等构造出的q元量子MDS码的基础上，给出了几类q元量子MDS码的具体实例，这些量子MDS码具有码长(q+1)(q-1)/m，其中m整除(q+1)(q-1)，但m不整除q-1，也不整除q+1.

量子纠错编码；量子MDS码；Hermitian内积

0　引　言

本文主要从参考文献[20]的最后一类q元量子MDS码出发，考虑此类q元量子MDS码的相关参数，给出了一些新的量子MDS码.

1　预备知识

本节将给出一些基本定义和性质，以及现有的q元量子MDS码的结果.令q为一个奇素数的方幂，Fq表示具有q个元素的有限域.

1.1线性码

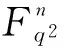
1.2量子MDS码

如何构造q元量子MDS码最近成为研究热点.比较常用的构造q元量子MDS码方法是Hermitian方法，见如下定理.

定理1.1[2]如果存在一个有限域Fq2上参数为[n,k,d]q2的MDS码C，而且C⊆C⊥H,则可构造出一个q元量子MDS码[[n,2k-n,≥d]]q.

通过这个定理，可由Reed Solomon码、循环码、negacyclic码、constacyclic码这些经典的MDS码构造出很多q元量子MDS码，此外选择具有较大最小距离d的Hermitian自正交MDS码，便可以得到具有较大最小距离的q元量子MDS码.文献[20]直接给出具有Hermitian正交线性MDS码的生成矩阵，再给出了几类q元量子MDS码.如下引理给出了如何使用相互Hermitian正交的行向量组成的生成矩阵产生Hermitian自正交码.

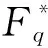
由引理1.1，只要给出一些相互Hermitian正交的行向量，便可以由这些行向量组成的生成矩阵给出Hermitian自正交码.要使用此方法构造q元量子MDS码，还需要Hermitian自正交码达到Singleton界，即需要Hermitian自正交的MDS码.文献[20]采用了类似多项式码的构造方法，考虑Fq2上所有次数小于某个数值的多项式，然后使用这些多项式在Fq2的生成元幂次上的赋值来给出Hermitian自正交的MDS码，通过此方法使用Hermtian自正交码可以得到q元量子MDS码，文献[20]的一些结果放在如下两个定理中.

定理1.2[14-15]设q为一个奇素数幂，偶数m为q-1的一个因子，则存在参数为[[n,n-2d+2,d]]q的量子MDS码q，其中n=(q2-1)/m，最小距离d满足2≤d≤(q+1)/2+(q-1).

定理1.3[20]设q为一个素数幂，偶数m1为q-1的因子，奇数m2为q+1的因子，则存在[[n,n-2d+2,d]]q的量子MDS码，其中n=(q2-1)(1/m1+1/m2+1/m1m2)，d满足2≤d≤(q-1)/2+min{(q-1)/m1+1,(q+1)/2m2}.

2　新的q元量子MDS码

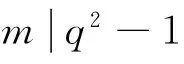
下面两个引理是文献[20]给出一类q元量子MDS码参数满足的条件和性质.

引理2.1[20]偶数m1与奇数m2互素，则存在无限个素数q使得m1整除q-1，m2整除q+1.

引理2.2[20]存在无限个正整数数对(m1,m2)满足以下条件：

1)m1是一个偶数，m2为一个奇数，gcd(m1,m2)=1；

2)(m1+m2-1)整除m1m2，令m=m1m2/(m1+m2-1)，且gcd(m,m1)>1，gcd(m,m2)>1.

由引理2.1和引理2.2知，满足这两个定理的条件的参数m和q具有无限多个，这两个定理并没有给出这些参数的具体实例.如下定理给出了由这些参数所决定的一类q元量子MDS码.

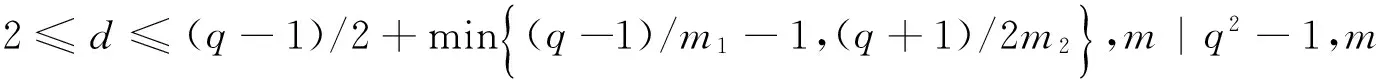
满足引理2.1和引理2.2的参数对m和q可以给出相应的q元量子MDS码，由引理2.2满足条件的参数m有无限个，由引理2.1给定参数m，有无限多个q满足条件，从而m和q的选取的无限性，可以得到无限个此类q元量子MDS码.通过研究引理2.1和引理2.2中参数对m和q满足的条件，给出如下5类满足引理2.1和引理2.2的数对(m,q)：

1)m1=k,m2=a(k-1),m=ak/(a+1),q=bk2-(b+2)k+1，其中q为奇数幂，k为偶数，a为奇数；

2)m1=ak,m2=k+1,m=a(k+1)/(a+1),q=bk2+(b+2)k+1，其中q为奇数幂，k为偶数，且(a+1)|(k+1),a|(bk+b+2)；

3)m1=2k,m2=ak+1,m=2(ak+1)/(a+2),q=2(ab-a2)k2+2bk+1，其中q为奇数幂，a,k为正整数；

4)m1=4k,m2=8k2-6k+1,m=4k-2,q=32ak3+8(2-3a)k2+4(a-3)k+1，其中q为奇数幂，a,k为正整数；

5)m1=akt,m2=(akt-1)(ak-1),m=kt-1(ak-1),q=2at+1k2t-2(a+at)kt+1，其中q为奇数幂，t≥2,a,k,t均为正整数，且akt,ak均为偶数.

这5类参数对(m,q)可以由相关的整数变量给出.给出相关变量的值，就可以确定数对(m,q)，每一类都可以给出无限个参数对(m,q).一般情况下，通过多项式变换f:k→f(k)求得更多的数对(m1,m2)，其中多项式f(k)∈Z[X]，从而得到更多的参数对(m,q).由定理1.2和定理2.1，可得到相应的q元量子MDS码[[n,n-2d+2,d]]q，其中码长为n=(q2-1)/m.在上面给出的5类参数中，取定变量的值，得到相应的5类具体的参数组：

1)k=8,a=3,b=1,m1=8,m2=21,m=6,q=41,n=280；

2)k=8,a=2,b=6,m1=16,m2=9,m=6,q=449,n=33 600；

3)k=8,a=1,b=1,m1=16,m2=9,m=6,q=17,n=48；

4)k=2,a=5,m1=8,m2=21,m=6,q=881,n=129 360；

5)k=2,a=3,t=2,m1=12,m2=55,m=10,q=769,n=59 136.

将这些参数组应用到定理1.2和定理2.1，得到相应的q元量子MDS码，具体见表1和表2.

表1　由定理2.1得到的q元量子MDS码

表2　由定理1.2得到的q元量子MDS码

3　结束语

量子MDS码有很强的纠错能力，可以相对容易地编码和译码，具有很强的实用性.构造较大最小距离的q元量子MDS码是量子码中一个重要的问题.本文在文献[20]的基础上，研究了一类q元量子MDS码的构造方法和相关参数，可以给出5类这种量子MDS码的参数组，从而得到具体的最小距离大于q/2的q元量子MDS码.这些具体参数的量子MDS码可以方便地应用于量子通信中.如何构造更多量子MDS是量子码理论和实际应用研究的热点.

[1]ALYSA,KLAPPENECKERA,SARVEPALLIPK.OnquantumandclassicalBCHcodes[J].InformationTheory,IEEETransactionson, 2007,53(3):1183-1188.

[2]ASHIKHMINA,KNILLE.Nonbinaryquantumstabilizercodes[J].InformationTheory,IEEETransactionson, 2001,47(7):3065-3072.

[3]ASHIKHMINA,LITSYNS.Foundationsofquantumerrorcorrection[J].AMSIPSTUDIESINADVANCEDMATHEMATICS, 2007, 41: 151 -185.

[4]ASHIKHMINA,TSFASMANMA,LITSYNS.Asymptoticallygoodquantumcodes[J].PhysicalReviewA,2000, 63(3):222-224.

[5]BIERBRAUERJ,EDELY.Quantumtwistedcodes[J].JournalofCombinatorialDesigns, 2000, 8(3): 174-188.

[6]FENGK,LINGS,XINGC.Asymptoticboundsonquantumcodesfromalgebraicgeometrycodes[J].InformationTheory,IEEETransactionson, 2006,52(3):986-991.

[7]GRASSLM,BETHT,ROETTELERM.Onoptimalquantumcodes[J].InternationalJournalofQuantumInformation, 2004, 2(1): 55-64.

[8]LAGUARDIAGG.Constructionsofnewfamiliesofnonbinaryquantumcodes[J].PhysicalReviewA, 2009, 80(4): 3383-3387.

[9]LAGUARDIAGG.NewquantumMDScodes[J].InformationTheory,IEEETransactionson, 2011,57(8):5551-5554.

[10]LAGUARDIAGG,PALAZZOR.ConstructionsofnewfamiliesofnonbinaryCSScodes[J].DiscreteMathematics, 2010, 310(21): 2935-2945.

[11]HAMADAM.Concatenatedquantumcodesconstructibleinpolynomialtime:Efficientdecodinganderrorcorrection[J].InformationTheory,IEEETransactionson, 2008,54(12):5689-5704.

[12]CALDERBANKAR,RAINSEM,SHORPW,etal.QuantumerrorcorrectionviacodesoverGF(4)[J].InformationTheory,IEEETransactionson,1996,44(4): 1369-1387.

[13]FENGK.Quantumcodes[[6, 2, 3]]pand[[7, 3, 3]]p (p ≥ 3)exist[J].InformationTheory，IEEETransactionson, 2002, 48(8):2384-2391.

[14]JINL,LINGS,LUOJ,etal.ApplicationofclassicalHermitianself-orthogonalMDScodestoquantumMDScodes[J].InformationTheory,IEEETransactionson, 2010,56(9):4735-4740.

[15]JIN L,XING C. A construction of new quantum MDS codes[J].Information Theory,IEEE Transactions on,2014,60(5):2921-2925.

[16]KAI X,ZHU S. New quantum MDS codes from negacyclic codes[J].Information Theory,IEEE Transactions on,2013,59(2):1193-1197.

[17]JIN L,XING C. Euclidean and Hermitian self-orthogonal algebraic geometry codes and their application to quantum codes[J].Information Theory,IEEE Transactions on,2012,58(8):5484-5489.

[18]CHEN B,LING S, ZHANG G.Application of constacyclic codes to quantum MDS codes[J]. Information Theory,IEEE Transactions on,2015,61(3):1474-1484.

[19]KAI X,ZHU S, LI P. Constacyclic codes and some new quantum MDS codes[J]. Information Theory,IEEE Transactions on, 2014,60(4):2080-2086.

[20]HE X, XU L,CHEN H. New q-ary Quantum MDS Codes with Distances Bigger than q/2[J]. arXiv preprint arXiv:1507.08355,2015.

A Class of New q-ary Quantum MDS Codes

NIU Gang, QI Yanfeng

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Quantum codes have applications in quantum computing and quantum communications. Quantum maximal distance separable(MDS) codes are a class of optimal quantum error-correcting codes and their parameters satisfy the quantum Singleton bound. The construction of quantum MDS codes has important application in theory and practice. It is still difficult to constructq-ary quantum MDS codes of length bigger thanq+1 with a big minimum distance. Manyq-ary quantum MDS codes of length (q+1)(q-1)/m have been constructed, wheremis a factor ofq+1orq-1. This paper uses some results in [20] and presents some quantum MDS codes of length (q+1)(q-1)/m, where m is a factor of (q+1)(q-1), m is not a factor ofq+1 orq-1.

quantum error-correcting code; quantum MDS code; Hermitian inner product

10.13954/j.cnki.hdu.2016.05.019

2015-11-30

国家自然科学基金资助项目(11531002,11501154)

牛刚(1990-),男,山西长治人,硕士研究生,密码学.通信作者：亓延峰讲师，E-mail：qiyanfeng07@163.com.

TN911.22

A

1001-9146(2016)05-0095-04