张量广义高次特征值互补问题解的一个刻划

常肖蕊，凌　晨

(杭州电子科技大学理学院，浙江 杭州 310018)



张量广义高次特征值互补问题解的一个刻划

常肖蕊，凌晨

(杭州电子科技大学理学院，浙江 杭州 310018)

提出了一类张量广义高次特征值互补问题与非线性规划之间的等价关系.进一步给出了相应非线性规划问题的稳定点是张量广义高次特征值互补问题解的充要条件，最后，在特征值次数满足一定条件下，证明了张量广义高次特征值互补问题可被转化为张量高次特征值互补问题.

高阶张量；高次特征值互补问题；非线性规划；稳定点

0　引　言

矩阵特征值互补问题是一类特殊的非线性互补问题，它具有广泛的应用背景[1-2].张量特征值互补问题是矩阵特征值互补问题的推广，其求解是一个困难问题.通常将张量特征值互补问题转化为等价的非线性规划问题来求解[3].本文提出了一类更为一般的张量广义高次特征值互补问题，并刻划该问题解的特征，从而说明在一定条件下求解此问题可转化成求解一类非线性优化问题的稳定点.进一步，在若干特殊情形下，张量广义高次特征值互补问题可转化为张量高次特征值互补问题.

1　概念与问题

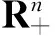
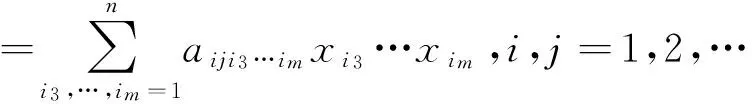
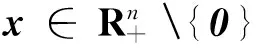
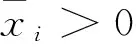
本文考虑以下形式的张量广义高次特征值互补问题(简记TGHDEiCP)，存在实数λ∈R和向量x∈Rn{0}，使得

(1)

若(λ,x)满足式(1)，则称λ为(A,B,C)的(k,l)次特征值，x为(A,B,C)的属于λ的特征向量.此时，也称(λ,x)为(A,B,C)的(k,l)次特征对.这里，m是偶数，而k和l为满足m≥k>l≥1的自然数.显然，若m=2，则k=2和l=1，此时上述问题即为矩阵的二次特征值互补问题.若A=0，记上述问题为张量高次特征值互补问题(THDEiCP)，它与张量特征值互补问题(TEiCP)密切相关，此时称(λ,x)为(B,C)的l次特征对.

众所周知，张量特征值问题与多项式优化关系密切.下面，研究TGHDEiCP的非线性规划转化形式并以此刻划TGHDEiCP解的特征.

2　主要结果

针对A，B,C∈Tm,n考虑非线性规划

minf(x,y,z,w,λ)

s.t.w-A zm-1-Bym-1-C xm-1=0,

xTe=1,

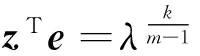
x≥0,w≥0.

(2)

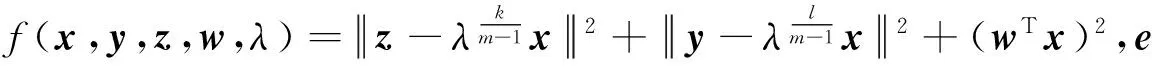
(3)

称满足式(3)的(x,y,z,w,λ)为式(2)的稳定点，并称(α,η,δ,β,γ)为相应的Lagrange乘子.

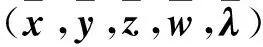
(4)

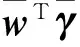
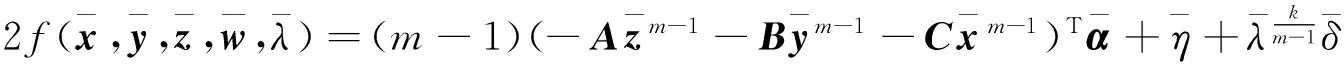
(5)

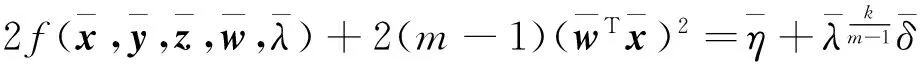
(6)

下面讨论TGHDEiCP与式(2)的解之间的关系.

定理1设A, B, C∈Tm,n.则(A, B, C)有(k,l)次特征对，当且仅当式(2)有目标函数值为0的全局最优解.

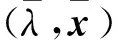
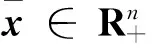
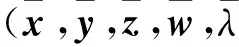
上述定理表明，求解TGHDEiCP可等价转化成求解非线性规划的全局最优解.然而，求解非线性规划的全局最优解仍是一件困难任务，下面的定理进一步建立了全局最优解与稳定点之间的关系.

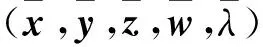
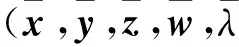
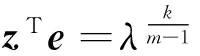
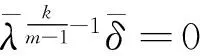
(7)

张量特征值互补问题和通常的张量高次特征值互补问题都是特殊的互补问题，利用投影算法和交替方向算法可分别有效求得它们的解[3,7].下面讨论TGHDEiCP与THDEiCP的关系.

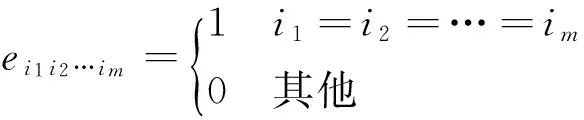
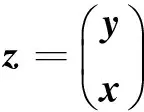
即

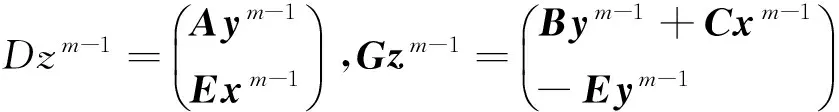
(8)

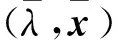
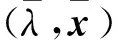
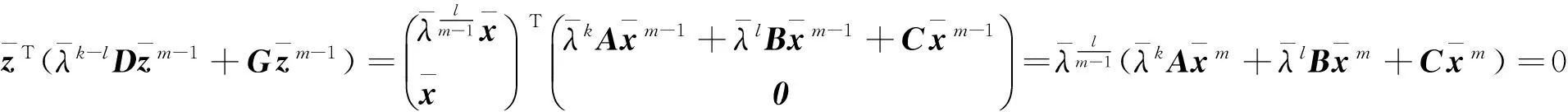
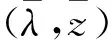
由式(8)知

(9)

进一步由式(9)知

(10)

从而由式(10)中第2式知

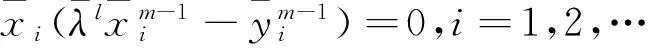
(11)

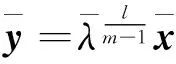
3　结束语

本文首先研究了一类张量广义高次特征值互补问题的非线性规划转化形式，将所考虑的张量广义高次特征值互补问题的求解转化为相应多项式优化问题的全局最优解的求解.进一步，刻划了优化问题的稳定点是张量广义高次特征值互补问题解的充要条件.同时，在特征值次数满足k=2l的情形下，本文证明了张量广义高次特征值互补问题可以被转化为相对较易求解的张量高次特征值互补问题.这些结果均为以后设计求解张量广义高次特征值互补问题算法提供了新途径.

[3]LINGC,HEH,QIL.Ontheconeeigenvaluecomplementarityproblemforhigher-ordertensors[J].ComputationalOptimizationandApplications, 2016, 63(1): 143-168.

[4]COMONP,MOURRAINB.Decompositionofquanticsinsumsofpowersoflinearforms[J].SignalProcessing, 1996, 53(2/3):93-107.

[5]QIL.Eigenvaluesofarealsupersymmetrictensor[J].JournalofSymbolicComputation, 2005, 40(6): 1302-1324.

[6]QIL．Symmetricnonnegativetensorsandcopositivetensors[J]．LinearAlgebra&itsApplications, 2013, 439 (1):228-238．

[7]LINGC,HEH,QIL.Higher-degreeeigenvaluecomplementarityproblemsfortensors[J].ComputationalOptimization&Applications,,2016, 64(1):149-176.

A Characterization of Solutions of Tensor Generalized Higher-degree Eigenvalue Complementarity Problem

CHANG Xiaorui, LING Chen

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

This paper proposes an equivalence relation between the considered tensor generalized higher-degree eigenvalue complementarity problem and nonlinear programming problems. Furthermore, a necessary and sufficient condition for the stationary point of the corresponding nonlinear programming problem being the solution of the tensor generalized higher-degree eigenvalue complementarity problem is given. Finally, under the degree of eigenvalues satisfies certain conditions, it is proved that the tensor generalized higher-degree eigenvalue complementarity problem can be transformed into the tensor higher-degree eigenvalue complementary problem.

higher-order tensor; higher-degree eigenvalue complementarity problem; nonlinear programming; stationary point

10.13954/j.cnki.hdu.2016.05.017

2016-03-11

国家自然科学基金资助项目(11571087)

常肖蕊(1991-)，女，河南濮阳人，硕士研究生，非线性优化.通信作者：凌晨教授，E-mail:macling@hdu.edu.cn.

O221.2

A

1001-9146(2016)05-0087-05