(k+2,k)的Hadamard极小存储再生码的明显修复方案

黄冬梅，唐春明，亓延峰

(1.西华师范大学数学与信息学院，四川 南充 637002；2.杭州电子科技大学理学院，浙江 杭州 310018)



(k+2,k)的Hadamard极小存储再生码的明显修复方案

黄冬梅1，唐春明1，亓延峰2

(1.西华师范大学数学与信息学院，四川 南充 637002；2.杭州电子科技大学理学院，浙江 杭州 310018)

(k+2,k)的Hadamard极小存储再生(MSR)码是一类对所有的失效单节点都具有最优修复属性的高码率纠删码.在已有研究工作的基础上，本文进一步研究一些矩阵的特殊结构,并借助Hadamard设计的基本性质，给出了一些大型矩阵的逆矩阵，获得了(k+2,k)的MSR码在单节点失效时的明显修复方案，从而使得(k+2,k)的MSR码的更加有效应用.

分布式存储；Hadamard设计；纠删码；明显修复方案；MSR码

0　引　言

随着大数据时代的来临，各种超大规模的分布式存储系统得到迅速发展.为了维护数据的可靠性和抵抗数据丢失的能力，数据恢复是系统必须具备的基本能力，主要是利用数据副本和纠删码两种冗余机制来维持分布式系统数据的修复能力.由于纠删码高效的数据存储效率，一些著名系统采用了基于纠删码的存储，例如Google Colossus(GFS2)[1]、Microsoft Azure[2]、HDFS Raid[3]和OceanStore[4].若分布式系统中节点数据丢失，为了维持系统的冗余水平，必须重构该节点的数据.有许多指标衡量节点修复的代价，例如从磁盘中总共读取的信息量，网络中总的通信量(修复带宽)，或者每次修复所需的磁盘数，其中最重要的是修复带宽.文献[5]给出存储量和修复带宽之间的折中关系，实现极小存储的极大距离可分码被称为极小存储的再生码(MSR).文献[6-7]构造出低码率情形下MSR码.文献[8-9]在高码率情形下给出明显的MSR码，但只对系统节点具有最优的修复性质.文献[10]基于Hadamard设计给出了一种明显的(k+2,k)的MSR码，它对所有的节点(系统节点和校验节点)都有最优的修复性质，称这种码为(k+2,k)的Hadamard MSR码.文献[11]利用Hadamard设计性质，改进了文献[10]的修复策略，大幅度降低单节点修复的计算量.但已有修复方案需要求解某些大规模线性方程组，计算费时.本文继续使用文献[11]的Hadamard设计的基本性质，给出了一些大型矩阵的逆矩阵，并在单节点失效时给出了(k+2,k)的MSR码的明显修复方案.

1　预备知识

表1　(k+2,k)的Hadamard MSR码

表1中前k个系统节点存储原始数据，第1个校验节点存储原始数据的和，第2个校验节点存储原始数据的线性组合，相关系数为

(1)

为了高效地修复失效的单节点，文献[11]引入了如下几个重要的稀疏矩阵.

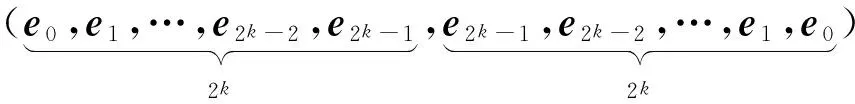
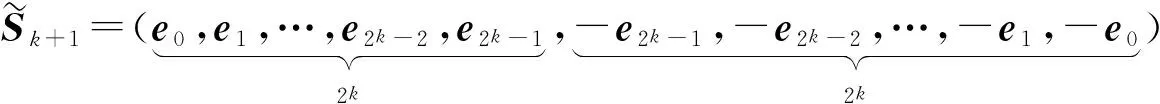
(2)

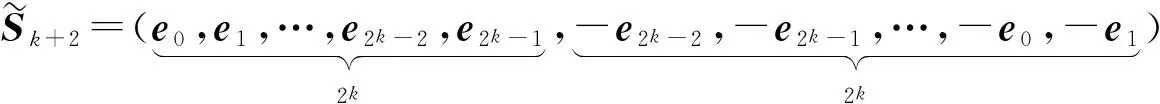
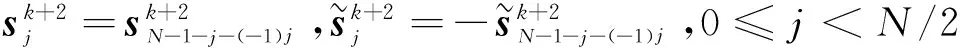
2　(k+2,k)的Hadamard极小存储再生码的明显修复方案

本节给出一些逆矩阵的结果，并对系统节点和校验节点给出了明显修复方案.下面引理是对文献[11]相关结果的一个总结.

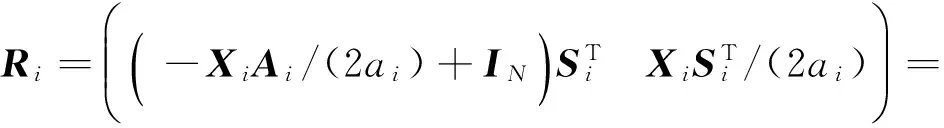
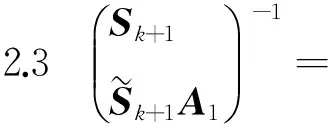
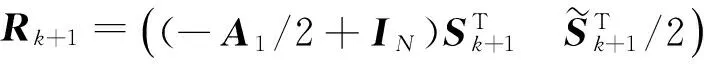
类似引理2.2证明，使用引理1.1，同理可证明此引理.

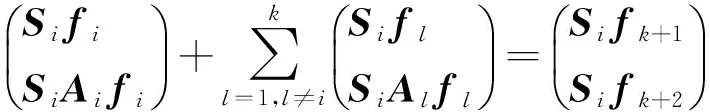
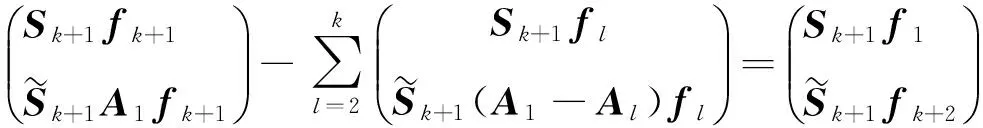
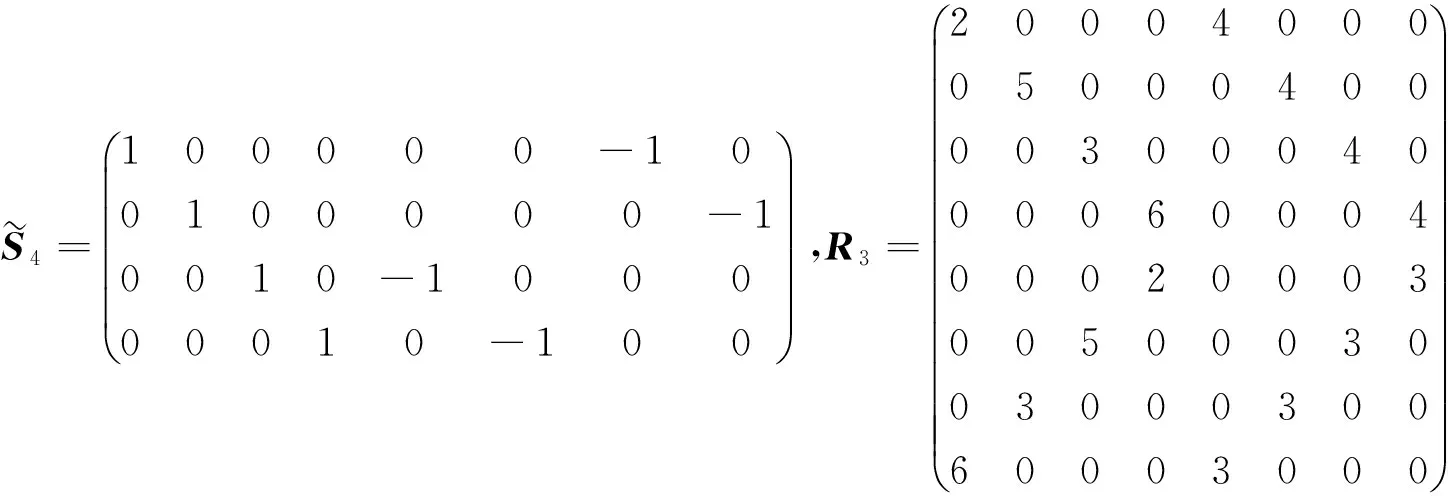
3　结束语

本文通过计算一些大型矩阵的逆矩阵，并借助Hadamard设计的基本性质，给出了(k+2,k)的MSR码在单节点失效时的明显修复方案，适用于系统节点和校验节点，从而使得(k+2,k)的MSR码更加实用，在分布式存储系统中有着重要的应用价值.

[1]QUORA.Google-GFS2Colossus[EB/OL]. [2016-02-09].http://www.quora.com/Colossus-Google-GFS2.

[2]HUANGC,SIMITCIH,XUY,etal.Erasurecodinginwindowsazurestorage[C]//Presentedaspartofthe2012USENIXAnnualTechnicalConference(USENIXATC12), 2012: 15-26.

[3]HADOOPWiki.HDFSRAID[EB/OL]. [2016-02-09].http://wiki.apache.org/hadoop/HDFS-RAID.

[4]KUBIATOWICZJ,BINDELD,CHENY,etal.OceanStore:anarchitectureforglobal-scalepersistentstorage[J].AcmSigplanNotices, 2000, 35(11):190-201.

[5]DIMAKISAG,GODFREYPB,WUY,etal.Networkcodingfordistributedstoragesystems[J].InformationTheory,IEEETransactionson, 2010, 56(9):4539-4551.

[6]SHAHNB,RASHMIKV,KUMARPV,etal.InterferenceAlignmentinRegeneratingCodesforDistributedStorage:NecessityandCodeConstructions[J].InformationTheory,IEEETransactionson, 2010, 58(4):2134-2158.

[7]SUHC,RAMCHANDRANK.Exact-repairMDScodesfordistributedstorageusinginterferencealignment[C]//2010IEEEInternationalSymposiumonInformationTheory.IEEE, 2010: 161-165.

[8]TAMOI,WANGZ,BRUCKJ.Zigzagcodes:MDSarraycodeswithoptimalrebuilding[J],InformationTheory,IEEETransactionson, 2013, 59(3): 1597-1616.

[9]LIJ,TANGX,PARAMPALLIU.Aframeworkofconstructionsofminimalstorageregeneratingcodeswiththeoptimalaccess/updateproperty[J].InformationTheory,IEEETransactionson, 2015, 61(4): 1920-1932.

[10]PAPAILIOPOULOSDS,DIMAKISAG,CADAMBEVR.Repairoptimalerasurecodesthroughhadamarddesigns[J].InformationTheory,IEEETransactionson, 2013, 59(5): 3021-3037.

[11]TANGX,YANGB,LIJ,etal.ANewRepairStrategyfortheHadamardMinimumStorageRegeneratingCodesforDistributedStorageSystems[J].InformationTheory,IEEETransactionson, 2013, 61(10):5271-5279.

Concrete Optimal Repair Strategy for (k+2,k) Hadamard Minimum Storage Regenerating Codes

HUANG Dongmei1, TANG Chunming1, QI Yanfeng2

(1.SchoolofMathematicsandInformation,ChinaWestNormalUniversity,NanchongSichuan637002,China;2.SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

The (k+2,k) Hadamard minimum storage regenerating(MSR) code is a high rate storage code with optimal repair for all single node failures. This paper uses the techniques of Tang et al.’s work and properties of Hadamard designs, gives inverses of some special matrices, and presents concrete, efficient, and optimal repair computation for all the single nodes failures.

distributed storage systems; Hadamard design; erasure codes; optimal repair; MSR codes

10.13954/j.cnki.hdu.2016.05.016

2016-03-09

国家自然科学基金资助项目(11401480)

黄冬梅(1980-)，女，湖北荆州人，助教，组合优化与编码.

TP309.3

A

1001-9146(2016)05-0082-05