ARIMA模型在卫星的可靠性评估中的应用

高　慧，程宗毛

(杭州电子科技大学理学院，浙江 杭州 310018)



ARIMA模型在卫星的可靠性评估中的应用

高慧，程宗毛

(杭州电子科技大学理学院，浙江 杭州 310018)

利用运行卫星的太阳能电池的电流数据对电池的可靠性进行了定量探究，建立ARIMA(5，1，4)非平稳时间序列分析模型.基于建立的时序模型，给出了对卫星太阳能电池退化量的预测方法，并建立了太阳能电池的可靠度方程.通过实例验证了方法的有效性和可行性，且基于实例编制了相应的R的程序.

可靠性；ARIMA模型；R软件；预测

0　引　言

卫星可靠性与人身安全联系较为密切，对卫星的发射而言，一旦发生失效，后果将不堪设想，因此对于卫星发射系统来说，可靠性的评估具有深远的意义，而卫星可靠性尤为密切的是卫星的太阳能电池.传统的可靠性建模评估方法对卫星太阳能电池高可靠性这类长寿命的产品束手无策，需要一种新的可靠性评估方法.文献[1]用时间序列方法对部件实时可靠性进行建模，以反映单一部件的实时可靠性；文献[2]在假设退化量分布为正态时，给出了基于性能退化数据的半似然可靠性预计方法；文献[3]采用Bootstrap仿真方法建立了动量轮寿命分布的模型，评价其可靠性水平.合理的时间序列模型可以对数据的发展趋势进行有效预测.本文采用ARIMA(p,d,q)模型对卫星电池寿命进行了预测，并对卫星的太阳能电池可靠性进行定量评估.

1　基于ARIMA模型的可靠性评估方法

1.1ARIMA模型理论

差分自回归移动平均模型(ARIMA)是自回归移动平均模型(ARMA)的扩展，运用ARIMA模型主要用于解决非平稳时间序列的预测分析问题.

1)ARIMA模型

ARIMA模型定义如下[4]：

(1)

其中，Φ(B)=1-φ1B-…φpBp为平稳的可逆ARIMA(p,q)模型的自回归系数多项式，Θ(B)=1-θ1B-…θqBq为平均可逆ARIMA(p,q)模型的滑动平均系数多项式，d=(1-B)d，B为后移算子，{εt}为均值为0时的白噪声.

2)自相关函数和偏相关函数

(2)

(3)

(4)

1.2ARIMA模型做预测操作流程图

ARIMA模型预测操作流程图如图1所示.

图1　ARIMA模型预测操作流程图

1.3可靠性分析

根据文献[5]可得在时刻tj的可靠度表达式为：

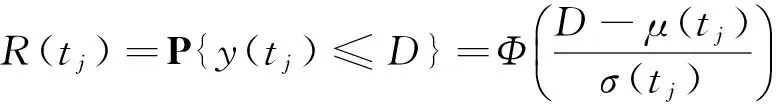
(5)

其中，y(tj)是在时刻tj的数据，D为失效阀值，μ(tj)，σ(tj)分别是在tj时刻的期望和标准差.

2　应用实例

本文研究的卫星太阳电池电流每月的平均值Xt，由浙江大学提供数据，时间跨度从2010年9月至2015年3月，共55个数据.选取2010年9月至2014年12月的52个数据作为建模样本，2015年1月至2015年3月的3个数据作为测试样本来评论样本的准确性.2010年9月至2014年12月电流的数据如图2所示.

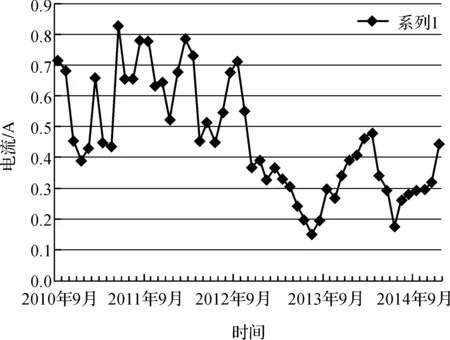
图2　卫星太阳能电池电流的每月平均数据

由R软件的adf.test知pvalue=0.260 1，从而数据为非平稳序列[6].接着对数进行一阶差分得到新序列Yt然后在进行检验，pvalue=0.021 17，可认为Yt是平稳序列.

由以上的ADF检验可知d=1，运用R语言对平稳序列做自相关函数和偏自相关函数分析，确定ARIMA(p,1,q)模型中的阶数p，q.新序列的自相关函数和偏相关函数如表1所示.

表1　Yt的自相关函数值和偏相关函数值

由表2可以看出，自相关和偏相关函数都是拖尾的，因此可以建立ARMA模型.计算所有模型的AIC值，当p=5,q=4的时，AIC值最小.故确定模型为ARIMA(5，1，4).

用R软件对模型的参数进行最小二乘法估计，得到估计参数的结果如表2所示.

表2　ARIMA(5,1,4)模型的参数估计

由上述结果预测后3个月的太阳能电流值如表3所示.

表3　真实值和ARIMA(5，1，4)模型预测表的比较

对模型进行残差检验，用R软件得到残差如图3所示.

由预测的结果和残差图可以看出，预测误差比较小，模型的残差值表现得较为平稳，模型的适应性检验是成立的,所以此模型是正确的.下面为了检验这个模型的效果，根据预测误差的时间曲线图和直方图，检验预测误差是否是平均值为零且方差为常数的正态分布.用R软件得到预测误差如图4所示.

图3　预测残差图

图4　预测误差的直方图

由图4预测误差的直方图可以看出，方差大致为常数(大致不变)(尽管上半部分的时间序列方差看起来稍微高一些).时间序列的直方图显示预测误大致是正态分布的且平均值接近0.因此，把预测误差看作平均值为0方差为常数正态分布是合理的.

由于任意阶数的ARMA模型均可由高阶自回归模型来描述，因此可采用AR(p)模型进行预测，利用上述的预测模型得到：

μ(tj)=-0.058 1μ(tj-1)-0.442 8μ(tj-2)+0.429 3μ(tj-3)-0.305 7μ(tj-4)-0.070 5μ(tj-5)在ARIMA(5,1,4)模型中σ(tj)的预测模型的表达式σ(tj)=0.304 1σ(tj-1)+0.530 5σ(tj-2)-0.888 7σ(tj-3)+0.188 9σ(tj-4).

由模型的预测方程可求出各时刻的分布参数值，假设太阳能电池的阀值为0.8，产品tj时刻可靠度表达式为：

由R软件和上面的可靠度的表达式，得到后3个月的可靠度如表4所示.

表4　可靠性预测值

由此可以看出，此模型预测后3个月的可靠度是比较准确的.

3　结束语

基于ARIMA建模的可靠性分析是一种估计可靠部件或系统可靠性的有效方法.本文对卫星太阳能电池的退化进行了建模领域的相关理论叙述和实践作了阶段性的总结.针对卫星太阳能电池的电流数据，建立电流变化的ARIMA模型，指出建模方法的适用性，给出了太阳能电池性能可靠性评估结果，获得比较理想的预测结果.

[1]LUH，KOLARIKWJ,LUSS.Real-timePerformanceReliabilityPrediction[J].Reliability,IEEETransactionson, 2001, 50(4): 353-357.

[2]JAYARAMJSR,GIRISHT.Reliabilitypredictionthroughdegradationdatamodelingusingaquasi-likelihoodapproach[C]//ReliabilityandMaintainabilitySymposium, 2005.Proceedings.Annual.IEEE, 2005:193-199.

[3]金光,刘强．基于性能退化的动量轮可靠性建模与评估[J]．数学的实践与认识，2009，39(15)：67-72.

[4]朱玉,王静.单纯ARIMA模型和ARIMA-GRNN组合模型在猩红热月发病率中的预测效果比较[D].合肥:安徽医科大学硕士论文,2011,35-41.

[5]BOXGEP,JENKINSGM,REINSELGC.时间序列分析:预测与控制[M].王成璋,尤梅芳,郝杨,译.北京：机械工业出版社，2011:57-209.

[6]尤琦，赵宇，马小兵.基于时序模型的性能退化数据可靠性评估[C]//中国现场统计研究会第十三届学术年会论文,2008.

[7]CRYERJD,CHANKS．时间序列分析及应用[M].潘红宇，王玲玲，李瑶帆，译.2版.北京：机械工业出版社，2011：77-152.

The Application of ARIMA Model of Satellite Reliability Assessment

GAO Hui, CHENG Zongmao

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Using the operation of satellite solar cell current data analyses quantitative explore for reliability of the battery, the ARIMA model is established to analyze the data of solar cell current. Based on the above time series model, this model has finished the prediction of performance degradation volume and established the reliability equation. The validity and feasibility of the method are verified by an example. The example obtains programs corresponding procedures on basis of R.

reliability; ARIMA model; R software; prediction

10.13954/j.cnki.hdu.2016.05.015

2015-12-23

高慧(1990-),女,安徽宿州人,硕士研究生,统计学.通信作者:程宗毛副教授，E-mail:zmcheng@hdu.edu.cn.

O213

A

1001-9146(2016)05-0077-05