一类修正的q-Baskakov-Beta算子的逼近性质

刘蕊蕊，胡晓敏，吴华亭

(杭州电子科技大学数学研究所，浙江 杭州 310018)



一类修正的q-Baskakov-Beta算子的逼近性质

刘蕊蕊，胡晓敏，吴华亭

(杭州电子科技大学数学研究所，浙江 杭州 310018)

q-Baskakov-Beta算子作为q-Baskakov算子的变形算子具有许多优良的性质.介绍了一类新的修正的q-Baskakov-Beta算子，通过计算得出了该算子的各阶矩，并讨论了其矩估计；研究了该算子的逼近性质，证得该算子有界且收敛.

q-Baskakov-Beta算子；K-泛函；光滑模；逼近

0　引　言

Baskakov算子作为算子逼近的一个重要分支，在函数逼近论中占有重要地位，已有大量的研究成果.近年来，文献[1]提出了q-Baskakov算子，并研究了该算子的逼近性质.在此之后，很多学者对q-Baskakov算子进行研究，得出了其变形算子，文献[2]在文献[3]的基础上首先提出了q-Baskakov-Beta算子.本文是在文献[2]的基础上，给出一类修正的q-Baskakov-Beta算子，采用文献[4]中相同的证明方法对其逼近性质进行了研究，得出了该算子具有有界性和收敛性.

1　基本概念和引理

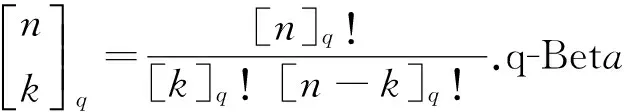
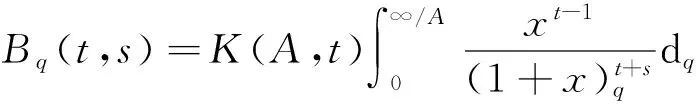
(1)

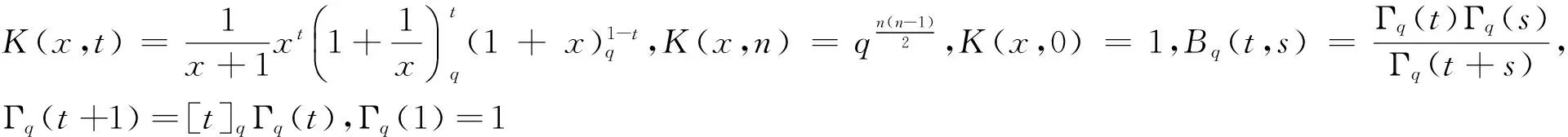
K-泛函[6]为：

(2)

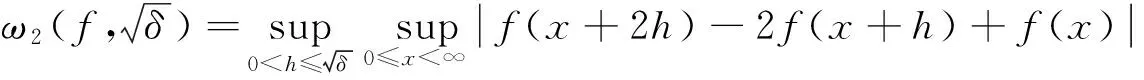
(3)

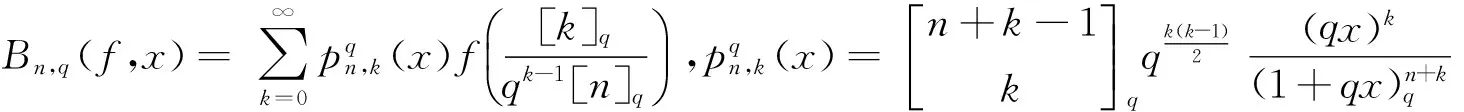
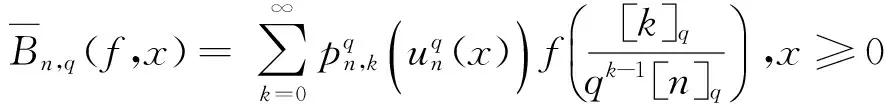
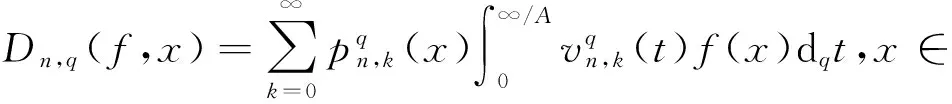
本文主要讨论定义4中修正的q-Baskakov-Beta算子的逼近性质，先看一些引理.

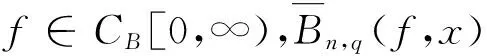
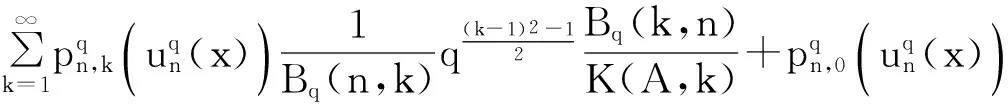
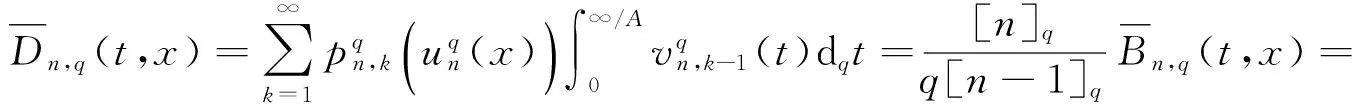
2　主要结果

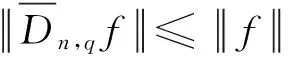
证明由定义4可知

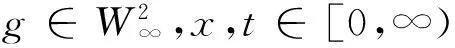
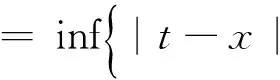
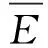
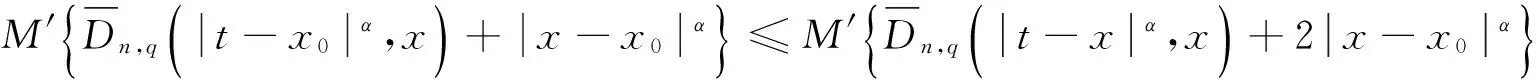
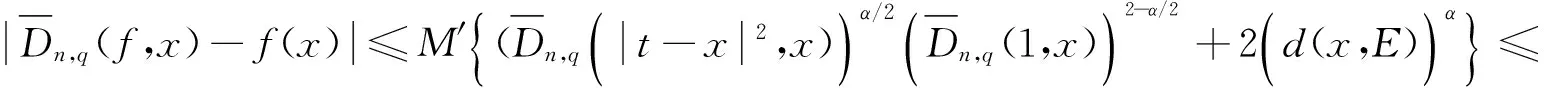
3　结束语

本文在文献[2]的基础上，给出了一类新的修正的q-Baskakov-Beta算子，利用K-泛函和光滑模研究了该算子的逼近性质，拓展了对一般的q-Baskakov-Beta算子的认识，为进一步研究这类修正型的算子有一定的意义.

[1]ARAL A, GUPTA V. Generalized q Baskakov operators [J]. Mathematica Slovaca, 2011, 61(4): 619-634.

[2]GUPTA V, ARAL A. Approximation by q Baskakov Beta operators [J]. Acta Mathematicae Applicatae Sinica, English Series, 2011, 27(4):569-580.

[3]王丽.修正的Baskakov-Beta算子的Voronovskaja型渐近展开公式[J].宝鸡文理学院学报(自然科学版)，2005，25(2):94-97.

[4]AGRAWAL P N, KUMAR A S. Approximation by q-Baskakov Durrmeyer type operators [J]. Rendiconti del Circolo Matematico di Palermo, 2014, 63(1):73-89.

[5]DE SOLE A, KAC V.G. On integral representations of q-gamma and q-betta functions[J]. Eprint Arxiv Math ,2003,16(1):11-29.

[6]DITZIAN Z, TOTIK V. Modulus of smoothness [M]. New York:Springer-Verlag, 1987:24-26.

Approximation Properties of the Modified q-Baskakov-Beta Operators

LIU Ruirui, HU Xiaomin, WU Huating

(InstituteofMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

The q-Baskakov-Beta operators have many better properties as the deformation of the q-Baskakov operators. This paper introduces a new modified q-Baskakov-Beta operators, gets the moments of this operators by calculating, and the moments estimation is discussed. It also investigates some kind of approximation properties of the operators, and gets that this operators with bounded and convergence.

q-Baskakov-Beta operators; K-functional; modulus of smoothness; approximation

10.13954/j.cnki.hdu.2016.05.020

2015-12-11

刘蕊蕊(1990-)，女，河南周口人，硕士研究生，函数逼近论.通信作者：胡晓敏副教授：E-mail：mathhuxm@163.com.

O174.41

A

1001-9146(2016)05-0099-04