基于不同残差分布的黄金波动率模型实证研究

赵崇增，郑　静，黄佩佩

(杭州电子科技大学理学院，浙江 杭州 310018)



基于不同残差分布的黄金波动率模型实证研究

赵崇增，郑静，黄佩佩

(杭州电子科技大学理学院，浙江 杭州 310018)

基于1988-01-02至2015-10-31每周伦敦现货黄金价格数据，按照条件异方差模型的建模步骤，对黄金收益率序列分别建立了残差服从标准正态分布、标准化学生t分布和广义误差分布的GARCH模型，并选取3个损失函数(均方根误差、平均绝对误差和泰勒不等系数)来检验模型预测效果的优劣.分析得出，对于伦敦黄金收益率序列，建立残差服从标准化学生t分布的GARCH模型，其样本内拟合效果和样本外预测精度都比较好.

黄金收益率；波动率；残差分布；GARCH模型

0　引　言

黄金是一种具有商品和货币双重属性的贵金属，是投资者资产保值增值的重要方式.近些年来，由于货币的不断贬值、通货膨胀压力不断增大、金融风险以及黄金的需求和供给等因素的影响，黄金价格波动明显增大.因此，建立有效的黄金价格序列模型能更好地解释和把握黄金价格的波动.

伦敦黄金交易具有悠久的历史，早在1804年，伦敦就已取代了阿姆斯特丹，成为了世界黄金的交易中心，1919年，伦敦黄金市场正式成立，到目前，伦敦已经是世界上最大的黄金交易市场，伦敦金价在世界黄金交易中已处于至关重要的领导和核心地位.

自从恩格尔突破性地提出了自回归条件异方差模型以来，基于GARCH的改进模型族已被广泛应用于黄金交易市场的预测与决策中.文献[1]对伦敦黄金年度数据用AR(2)过程进行拟合，并对伦敦黄金月度数据建立了TGARCH(1,1)模型，表明伦敦黄金波动存在杠杆效应；文献[2]利用R/S分析模型研究了国内外黄金价格波动特征，实证结果表明上海黄金和伦敦黄金价格波动均存在波动聚集和持续性的特征，且伦敦市场的上述特征更强；文献[3]对世界黄金价格序列分别拟合GARCH和SV-T模型,对比发现后者在对世界黄金价格走势的预测更优；文献[4]运用EGARCH模型特别研究了夜盘交易推出对国内黄金期货价格波动率的影响，结果显示,夜盘交易增加了市场的活跃度，却降低了平均波动率水平；文献[5]采用3种GARCH波动性模型研究黄金收益的波动行为，结果表明，FIGARCH(1，1)是预测黄金收益率波动性的最佳模型.本文结合以往国内外学者对黄金的研究，对黄金收益率序列分别建立了3种不同残差分布的GARCH模型，并选取适当的信息量和损失函数来检验模型的拟合和预测效果，主要探究残差服从哪种分布的GARCH模型能较好地描述伦敦现货黄金的尾部特征.

1　条件异方差模型及其残差分布

1.1GARCH模型

1982年,恩格尔突破性地提出了自回归条件异方差模型，简称ARCH模型.ARCH模型被认为是最能集中反映方差变化特点而被广泛应用于金融数据时间序列分析的模型，它的基本思想是扰动项的条件方差和它的前期值存在相关性.

为克服ARCH模型参数估计困难和估计精度不高的不足，Bollerslev提出了广义的ARCH模型(GARCH模型).GARCH(m，s)模型的一般形式如下：

(1)

其中，{εt}是均值为0、方差为1的独立同分布随机变量.

1.2GARCH模型的残差分布

金融时间序列一般具有厚尾的特性，而GARCH模型尾部太薄，因此需要模型的残差εt服从合适的厚尾分布，以此来达到准确描述金融收益率尾部特性的目的.通常情况下，残差εt假定服从标准正态分布、标准化学生t分布和广义误差分布.

1.2.1标准学生t分布

一般来说，对厚尾数据，残差εt服从标准化的学生t分布可能显得更合理.设随机变量εt服从学生t分布，自由度为v(v>2)，则εt的概率密度函数为

(2)

1.2.2广义误差分布

方差方程中的残差假定服从广义误差分布，其概率密度函数为

(3)

2　黄金收益率建模

2.1数据分析和处理

本文收集了1988-01-02日至2015-10-31每周伦敦现货黄金价格(单位：美元/盎司)，总共1 448个数据.数据来源于Wind资讯，文中所有算法的实现都是通过R语言来完成的.

对黄金价格数据作对数差分处理，得到黄金收益率序列，记为rt，其中，Pt为黄金在t时的价格.本文截取后30个收益率数据作为测试样本集，前面的1 417个数据构成训练样本集(记作rt).

黄金收益率时序图如图1所示.从中可以看出，收益率序列存在多个异常峰值，并且存在收益率波动集群现象，猜测序列波动可能存在条件异方差性.同时，通过计算得出收益率序列偏度为-0.142 4，超额峰度为4.786 8，说明了黄金收益率序列具有尖峰厚尾的特征.

图1　黄金收益率时序图

2.2模型建立

对黄金收益率进行建模，通过收益率序列的自相关图和偏自相关图对收益率序列建立符合AR(5)模型的均值方程，利用Engle的拉格朗日乘子法(ARCH-LM)对残差at进行滞后10阶的ARCH效应检验，检验p值接近于0，检验确认黄金收益率有很强的ARCH效应，因此，可以对收益率序列建立条件异方差模型.

根据方差方程中残差的不同分布，建立了3种不同的GARCH(1,3)模型，模型残差分别服从标准正态分布(norm)、标准化学生t分布(t)和广义误差分布(ged).对均值方程和方差方程进行联合估计，去掉均值方程不显著的参数，得到各个模型显著参数的极大似然估计量如表1所示.

表1　模型参数估计表

注：表格中括号内为参数估计的p值，AIC为模型的赤池信息量.

从表1中可以看出，残差服从标准学生t分布的GARCH模型的AIC是最小的，即样本内拟合效果最好.

2.3残差服从标准学生t分布的GARCH模型的研究

下面主要研究残差服从标准学生t分布的GARCH模型.根据模型参数估计表，写出残差服从标准学生t分布的AR(5)-GARCH(1,3)模型的具体形式为：

(4)

其中，εt服从自由度为7.50的标准化学生t分布.

所建立的GARCH模型的拟合波动率时序图如图2所示.分析模型的拟合波动率时序图可以发现，序列有少数比较高的峰值，这是跟当时的社会环境有一定的关系的，比如2000年的高波动率是和社会处于互联网泡沫期间有一定关联.

图2　残差服从标准学生t分布的GARCH模型的拟合波动率时序图

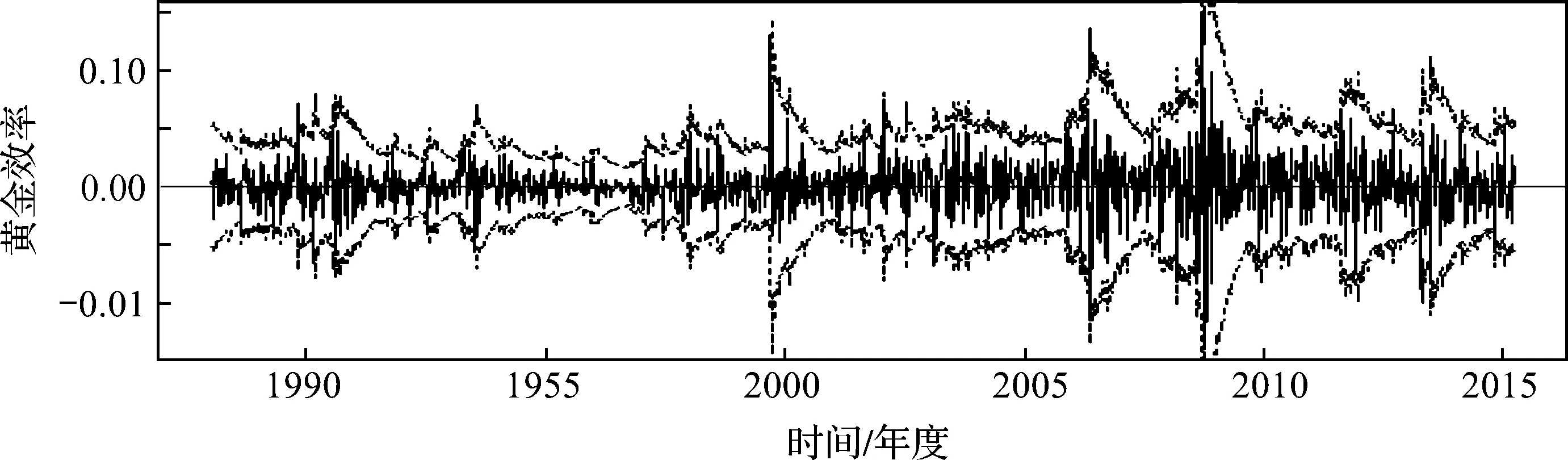
图3　黄金收益率时序图及残差服从标准学生t分布的GARCH模型的95%点预测区间

3　模型评价与结论

本文通过1988-01-02至2015-10-31每周伦敦现货黄金价格数据，按照金融时间序列条件异方差模型的建模步骤，对训练样本收益率数据建立了残差分别服从标准正态分布、标准化学生t分布和广义误差分布的GARCH(1,3)模型，分别对3个模型进行波动率预测.选择均方根误差(SRMSE)、平均绝对误差(SMAE)和泰勒不等系数(STIC)3个损失函数来检验预测效果，损失函数越小，预测的效果也就越好.损失函数的计算公式如下：

(5)

(6)

(7)

将模型的损失函数结果和模型的赤池信息量汇总分析，可以直观地看出模型的拟合效果.计算结果如表2所示.

由表2可知，残差服从标准学生t分布的GARCH模型AIC信息量和损失函数都比较小，因此，其样本内拟合效果和样本外预测精度都比较好.

4　结束语

本文的研究表明，基于标准学生t残差分布的GARCH模型能够较为准确地描述金融数据的波动率变化.这一模型不仅为金融市场的分析提供了理论依据，同时为投资者洞察市场发展变化规律、规避市场风险提供了重要手段.

[1]阚景阳.后危机时代国际黄金价格实证分析[J].上海金融学院学报,2015(4):15-23.

[2]温博慧.黄金价格波动性及其演化:以上海和伦敦市场为例[J].商业研究,2010(1):9-13.

[3]陈杨林,向东进.基于波动率模型的世界黄金价格实证分析[J].决策与信息(财经观察),2008(9):26-27.

[4]黄卓,李超.上海黄金期货波动率的实证分析—基于夜盘交易推出对黄金期货价格影响机制研究[J].价格理论与实践,2015(2):94-96.

[5]BENTES S R. Forecasting volatility in gold returns under the GARCH, IGARCH and FIGARCH frameworks: New evidence[J]. Physica A: Statistical Mechanics and its Applications, 2015, 438: 355-364.

An Empirical Study of the Gold Volatility Model with Different Residual Distribution

ZHAO Chongzeng, ZHENG Jing, HUANG Peipei

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

The paper chooses weekly gold spot price data of London from January 2, 1988 to October 31, 2015 to establish GARCH models with residuals subjected to the standard normal distribution, standard student’s t-distribution and generalized error distribution respectively, according to the modeling steps of conditional heteroskedasticity model. Then, it selects root mean square error, mean absolute error and Taylor coefficients as loss functions to test model predictions effect, and draws the conclusion that the GARCH model with residuals subjected to standard student’s t-distribution has a better ability of in-sample fitting and out-sample forecasting than others.

gold return; volatility; residual distribution; GARCH model

10.13954/j.cnki.hdu.2016.05.014

2015-12-11

赵崇增(1989-)，男，山东枣庄人，硕士研究生，统计学.通信作者：郑静副教授，E-mail：zhengjing@hdu.edu.cn.

F830.9

A

1001-9146(2016)05-0073-04