解析函数空间Hp,α的乘子性质

姜佳梅，肖建斌，张苏珍

(杭州电子科技大学基础数学研究所，浙江 杭州 310018)



解析函数空间Hp,α的乘子性质

姜佳梅，肖建斌，张苏珍

(杭州电子科技大学基础数学研究所，浙江 杭州 310018)

对Hp,α空间的乘子问题进行了研究，得到了单位圆盘上Hp,α空间到加权Bergman空间Ap,q,β乘子的一个充分条件；同时，还获得Cn中有界对称域上Hp,α空间到lq的乘子的一个充分条件，完善了有界对称域上Hp,α空间到lq的乘子性质.

单位圆盘；有界对称域；Hp,α空间；Ap,q,β；lq；乘子

0　引　言

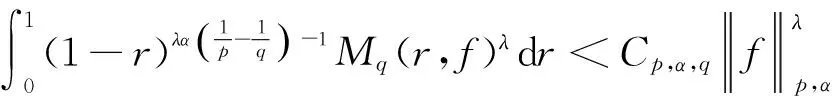
1　预备知识

记Ω为Cn中包含原点的有界对称域，用b表示它的Silov边界.记Γ是Ω的全纯自同构群，用Γ0表示Γ的使原点不变的子群，b上存在唯一的Γ0不变的测度σ，使得σ(b)=1.

文献[6]用群表示的方法构造了一组齐次多项式：

Cn中有界对称域上有关Hp,α空间的探讨，有系列成果，部分结果详见文献[7-8].

对于复序列{bk,v},v=1,2,…,mk,k=0,1,2…定义

(A,B)表示函数空间A到B的所有系数乘子的集合，即(A,B)={h∶h*g∈B,∀g∈A}.

2　主要定理

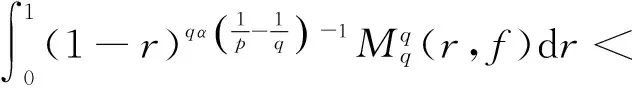
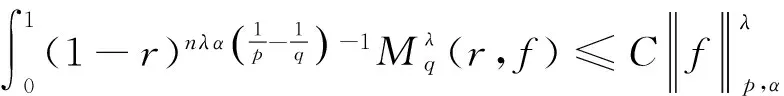
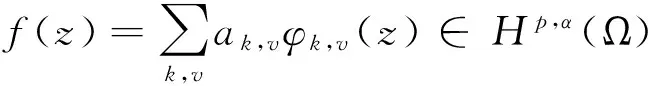
由引理4知

(1)

3　结束语

本文通过对Hp,α空间乘子性质的研究，得到了Hp,α空间到加权Bergman空间Ap,q,β乘子的一个充分条件，该条件的成立支持了文献[1]的猜想1成立；同时，还获得Cn中有界对称域上Hp,α空间到lq的乘子的一个充分条件.但如何证明文献[1]的猜想1，是下一步研究的方向.

[1]KIM H O, KIM S M, KWON E G, et al.A note on a spaceHp,αof holomorphic functions[J]. Bulletin of the Australian Mathematical Society,1987,35:471-479.

[2]肖建斌.Hp,α空间的Hardy Littlewood定理[J].数学进展,1995,24(2):139-144.

[3]史济怀.有界对称域上的Hardy-Littlewood定理[J].中国科学A辑,1988(4):366-375.

[4]李永群．Hp,α空间与Dp空间的函数性质[D]．长沙：湖南师范大学，2001．

[5]HARDY G H, LITTLEWOOD J E.Theorems concerning mean values of analytic or harmonic functions[J]. Quarterly Journal of Mathematics,1941,12(1): 221-256.

[6]华罗庚.多复变数函数论中的典型域的调和分析.北京:科学出版社,1965:143.

[7]张学军,关莹,李敏.单位球上对数权Bloch型空间的复合算子[J].数学进展,2015,44(4):553-561.

[8]刘竟成,张学军.单位球上小Bloch型空间之间的加权复合算子[J].数学物理学报,2010,30(4):894-907.

Some Multiplier Properties of Analytic Function SpaceHp,α

JIANG Jiamei, XIAO Jianbin, ZHANG Suzhen

(InstituteofFundamentalMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

This paper studies multiplier issues ofHp,αspace and gets a sufficient condition of multiplier fromHp,αspaces to weighted Bergman spaceAp,q,βon the unit disc. At the same time, this paper also obtains a sufficient condition of multiplier fromHp,αspace intolqon the bounded symmetric domains and this sufficient condition makes multiplier theorem ofHp,αspace complete.

unit disc; bounded symmetric domain;Hp,αspace;Ap,q,β;lq; multiplier

10.13954/j.cnki.hdu.2016.05.018

2016-04-05

国家自然科学基金资助项目(11571104)

姜佳梅(1989-)，女，安徽萧县人，硕士研究生，复分析.通讯作者:肖建斌教授,E-mail:xjb@hdu.edu.cn.

O174.5

A

1001-9146(2016)05-0092-03