从双基教学到数学核心素养
眭亚燕
绝大多数人都学过数学,但有关平方差的计算公式、一元二次方程的求根公式,长大后还有多少人能够记得?当这些东西都遗忘了,还能留在你脑海里的东西,就是素养.它不是为考试而设定的目标,而是对学生一生受用的方法和能力.在德育为先、素养为重、学问为本的社会主义教育学价值体系下,数学核心素养与数学课程的目标和内容直接相关,对于理解数学学科本质,设计数学教学,以及开展数学评价等有着重要的意义和价值.
一、侧重基础知识、基本技能素养
上世纪60年代以来,以“双基教学”为特征的我国数学教学理论体系逐渐形成.双基教学即注重基础知识、基本技能的教学和基本能力的培养,以教师为主导,以学生为主体,以学法为基础,注重教法,具有启发性、问题驱动性、示范性、层次性、巩固性的特征.
设计1:北师大版七(下)1.5平方差公式第一课时中,探究平方差公式这个知识点的教学设计:
2.平方差公式的结构特征是什么?
3.总结运用平方差公式进行计算的“三步法”:①变形:②套公式:③计算.
为什么学生在貌似掌握了平方差公式的比较抽象的数学符号语言,即(a-b)(a+b)=a2-b2之后,依然与完全平方公式(a±b)2= a2±2ab+b2相混淆呢?这不是简单的训练量的问题,而是学生头脑中没有很好建立平方差公式这个概念图式的原因.对于平方差公式来说,如果既不能这样用文字来表述:两个数的和与这两个数的差的积,等于这两个数的平方差.同时又不能广泛认识到平方差公式中的字母a、b不仅表示一个数或是单独的一个字母,还可以表示一个式子.倘若做不到这些,那么一切记忆依然是浮云.
二、加强基本思想、基本方法素养
在重视“双基教学”的口号下,一些学校大搞题海战术,只顾成绩,不管其它,加重了师生负担,造成应试教育和片面追求升学率的严重后果.为了改变这种情况, “三基教学”的概念相继出现,目的是在继承双基教学传统的基础上,进一步适应和体现时代的要求.三基教学即在注重基础知识、基本技能的教学和基本能力的培养之外,增加“基本思想和基本方法”.
设计2:苏科版七(下)9.4乘法公式第二课时中,探究平方差公式这个知识点的教学设计:
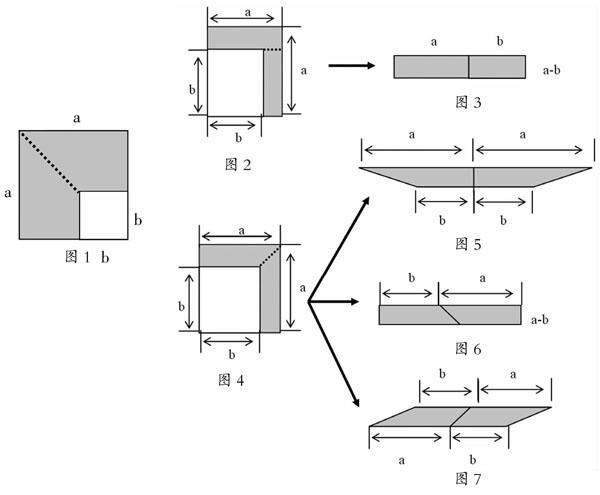
1.边长为b的小正方形纸片放置在边长为a的大正方形上,如下图,如何表示图中阴影部分的面积?
2.你能用多项式乘法运算法则推导公式(a-b)(a+b)=a2-b2吗?
在解答设计中的问题1时,我们综合运用了数形结合思想、转化思想和面积法等基本数学思想方法.其中数形结合思想是研究数学问题的有效途径和重要策略,它体现了数学的和谐美、统一美.华罗庚先生曾用“数缺形时少直觉,形少数时难入微”作高度的概括.如果把阴影部分看成是两个正方形的面积的差,那么它的面积为a2-b2,如果把阴影部分转化成两个梯形面积的和,那么它的面积为 ,这里我们借助几何图形特征将阴影部分面积问题转化为公式(a-b)(a+b)=a2-b2.但用面积推导法则有局限性(字母a、b表示正数),所以紧接着抛出问题2,用多项式乘法运算法则推导公式(a-b)(a+b)=a2-b2,至此,字母a、b可以表示任意数或式子.
三、积累活动经验、提升数学素养
随着新课标修订版的颁布,数学基本活动经验在课标中被列为“四基”之一,积累数学活动经验,提高学生教学素养,成了广大教师的共识.因此,教师要深入钻研教材,精心设计教学活动,帮助学生积累数学活动经验,提升学生数学素养.
设计3:新苏科版七(下)9.4乘法公式第二课时中,探究平方差公式这个知识点的教学设计:
1.在边长为a的大正方形纸片上剪去一个边长为b(b 2.沿图2中的虚线将阴影部分剪开拼成图3.由此,你发现了什么? 3.你还有其他剪拼图形的方法,计算图2中阴影部分的面积吗? 4.你能用多项式乘法运算法则推导公式(a-b)(a+b)=a2-b2吗? 设计问题2是引导学生通过动手操作,从图形的直观理解平方差公式的几何意义.设计问题3是用学生最喜欢的拼图游戏,引导学生从“形”的角度认识平方差公式的几何意义,真切的体会拼接的必然性和和其中蕴含的形状改变但面积不变的道理(梯形:如图5;矩形:如图6;平行四边形:如图7).学生在分割图形、剪拼图形的过程中,动脑、动手、探索交流,不仅获得了基础知识和基本技能,体会了数学思想,更重要的是积累了基本活动经验. 从双基教学的产生,到素质教育、情感态度价值观、学生学科核心素养等一系列理念的提出、研究和实施,不难发现,在这个变化发展的过程中,教育教学目标的实施一步步具体、明确、可操作,充分体现了基础教育科学研究的不断深入,体现了教育研究水平的不断提高.我们要深刻体会这种变化,最大限度地提高教学效率和教育质量,为现代化建设事业培养全面发展的合格接班人. 参考文献: 1.谢明初.数学教育中的建构主义[M].上海:华东师范大学出版社,2007:40. 2.胡梦甜.从数学学科看“核心素养”如何落地.浙江教育报,2015-11-20. 3.孙志刚.数学教学:从双基到学科核心素养.甘肃教育.2015:20

