数学作业讲评要注重“六性”

陆宇斐

[摘 要] 数学作业讲评是数学教学过程中不可或缺的重要一环。针对当前数学作业讲评中存在的低效讲评现象，提出数学作业讲评必须注重数学内容的准确性、数学语言的简洁性、数学思维的灵活性、数学认知的发展性、数学解题的方法性和数学学习的导向性的观点，旨在提升数学作业讲评的实效。

[关键词] 初中数学 作业评价 讲评课

作业讲评是数学教学的一环，认真设计、精心实施作业讲评是教师教学的“必修课”。但是，在当前数学课堂中，作业讲评普遍存在着形式单一不互动、就题论题不拓展、全部讲评无重点、一题一解不开放等误区。在这样的讲评课中，学生不仅收获甚微，而且加重了学习负担，也丧失了学习的兴趣。因此，数学作业讲评必须注重策略，科学地进行讲评。

一、纠正错误，注重数学内容的准确性

纠正错误是讲评的关键。分析错误原因是纠错的首要任务，剖析错误是作业讲评的重要内容之一。教师应把学生作业中的错误进行归纳、概括，找到通病和典型错误，找准其思维的薄弱点，有针对性地引导学生辨析，找准错因、错源，探究正确思路，做到触类旁通。使学生思维的严密性、批判性、灵活性、深刻性和创造性得到最有效的提高。针对学生练习中出现的共性问题，精心设计难度相当的练习题，加强有针对性的练习，使之强化，当堂反馈补救。

例如，在学习“平方差公式”时有这样一道作业题：计算（-x+y）（x+y）。学生做出了错误的解答：原式=x2-y2。这种错误是由于学生没有正确理解平方差公式的结构特征，将原题生搬硬套平方差公式所致。讲评时应该让学生找到平方差公式（a+b）（a-b）=a2-b2的结构特点：左边是两个二项式相乘，其中a与a是相同项，b与-b是相反项，右边是相同项与相反项的平方差的形式。在认清公式的结构特征的基础上，进一步剖析a、b的广泛含义。最后，让学生辨析下列各式能否运用平方差公式进行计算：①（2x+3y）（2x-3y），②（t2+1）（t2-1），③（-m+n）（-m-n），④[（a+b）+c] [（a+b）-c]。通过这样的讲评，学生在究错和纠错的过程中去伪存真，抓住了概念的核心，对公式由感性认识上升到理性认识，使学生在公式的运用中能得心应手，起到事半功倍的效果。

二、规范表达，注重数学语言的简洁性

学生做作业要按照数学学科的规范性进行，即解题的规范。总的要求是条理清晰、逻辑严密，准确使用数学语言。在数学作业的讲评中，要在确保学生审题准确的前提下，注意解题的逻辑性、严密性，在书写的清晰性、规范性、整洁性、美观性、简洁性等方面进行严格的要求和训练，容不得半点马虎，不能因为一字之差，而导致学生产生歧义。有些题目看起来简单，但它对解题的规范化提出了较高的要求。因此，数学教师必须做到教学语言严密、精炼、逻辑性强，在讲评时要注重这方面的问题，要给学生讲清讲透，让学生在以后的解题过程中始终想着这一点，在表达时做到简洁、规范。

例如，在解答几何证明题时，每一步推理的条件必须充分，注意推理过程必需严密、逻辑顺序合理、条理清楚。要把推理的过程写清楚，要明确每一步的推理依据。在叙述数学概念、定义和定理时要准确，不应使学生产生疑问或误解，不能随意误读。譬如，不能把“点到直线的距离”说成“点到直线的垂直距离”，否则会让学生误以为点到直线的距离除了垂直距离，还有非垂直距离；也不能把“垂线”说成“垂直向下的线”；不能把“最简分式”说成“最简单的分式”等。

三、交流想法，注重数学思维的灵活性

作业讲评中，对学生数学作业中的疑惑、想法、方法、思路、创见等进行交流是作业讲评中的重要内容。教师经常性的单独讲评往往会造成学生视觉和听觉的疲劳，容易滋生倦怠情绪，注意力也会分散，导致讲评效果不理想。由于对所评作业学生已独立思考解决过，学生或多或少已形成个人的认识，这就为教师“放手”提供了有利条件。

教师应努力营造民主、和谐的讲评氛围，相信学生，适时将教师主导下的“讲”改为师生共同参与下的“议”，让学生充分展示自己的想法，暴露思维的过程，包括典型错误的思考、巧妙的方法等，加之教师的引导、点拨，在质疑和争辩中实现作业问题的有效解决。作业讲评的信息也实现了从“单向传递”向“多向传递”的转变，能达到优劣互补、取长补短的目的。也可适时组织一些学生进行小组交流，小组内优生可以帮助中等生和后进生，中等生和后进生在这个过程中可以学习到优生的解题思路与方法，而优生同样也可以在别的同学身上发现自己的问题，在帮助别人的同时对自己也是一次检验。在此过程中，组内成员都有发表自己意见的机会，也有倾听别人想法的机会，在不知不觉中锻炼了自己与别人合作、交流的能力。

四、一题多变，注重数学认知的发展性

作业讲评过程中必须有训练的环节，可以在讲评之前练习，也可以讲评中间练习或是讲评之后练习。如果是重复性的机械式训练，学生必然会厌烦。而变式训练有利于提高学生积极参与讲评过程的热情，激发学生的求知欲望，提高作业讲评的有效性；有利于发掘学生的学习潜力，培养学生思维的广阔性与深刻性，提高学生的数学学习能力。

作业讲评时必须注意的是，变式训练要根据不同的讲评内容、讲评目标，合理地选择变式的方法。当作业中习题难度较高或学生基础较差时，可以通过习题的变式适当降低难度或设置一定的坡度以降低思维的起点，进行讲评之前的练习；当出现几个难点时，可在讲评之前或讲评之中通过习题的变式各个击破；而讲后练习的变式可依据拓展性原则，采用将作业题做情景变式、结论的变式、条件的变式、逆向变式、图形变式、解题方法变式、解题策略变式、解题思想变式等方法，以实现再现思路、拓展思路、获取新知、形成技能、找出规律、归纳方法、领悟思想、发展认知等讲评目标。总而言之，在作业讲评中教师要充分开发和利用作业中的习题，引发学生思考，透过现象寻找本质，从“变”的现象中发现“不变”的本质，从“不变”的本质中探究“变”的规律，灵活运用变式训练，提升作业讲评的有效性。

五、总结规律，注重数学解题的方法性

规律提炼是讲评的重点，作业中的题目仅仅是一个例子，所以只有帮助学生通过一道题弄清一类题解决的本质，引导学生掌握解题的规律，才能帮助学生开启知识宝库的大门。教师应将规律的总结作为作业讲评的重点。虽然规律是抽象的，但若在解题过程中详加钻研，还是能够发现规律的蛛丝马迹。在开拓解题思路、总结解题规律时，要抓住“通性通法”与特殊方法。通性通法是指具有普遍性和共性的常规解法，抓通法可以加深对知识、技能的理解和记忆，强化公式、法则的运用；特殊的方法和思路是根据问题的特殊性所产生的特殊的简便方法和思路，可以开启智慧大门，使能力得以升华。

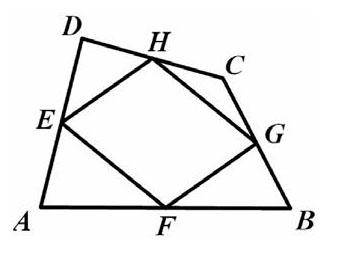
例如，有这样一道作业题：如图，顺次连接四边形ABCD各边中点，得四边形EFGH。要使四边形EFGH为矩形，应添加的条件是什么？在讲评此题时，先用“几何画板”工具进行演示，通过改变对角线AC、BD的位置关系与数量关系，让学生观察中点四边形EFGH的形状是如何变化的？它与原四边形ABCD的哪些量有关系？然后引导学生总结出规律：中点四边形的形状取决于原四边形对角线的位置关系与数量关系。分析完这道题后，再给出了以下2个巩固性练习题：（1）顺次连接等腰梯形各边的中点，所得到的四边形是什么？（2）顺次连接对角线互相垂直的等腰梯形各边中点，所得到的四边形是什么？

六、指导方法，注重数学学习的导向性

作业讲评中，教师要对学生的学习方法、解题方法和解题策略等进行指导。通过作业讲评使学生学会用批判的眼光去反思自己的解题过程，看看思路是否有问题，概念使用是否正确，计算是否有失误，思考是否周密等等。有时需要从不同的角度去思考，用不同的方法去演算更能发现问题，指导学生掌握解题具体方法，形成技能。

例如，解答选择题时可采用比较法、排除法、图像法、特殊值法；引导学生在分析问题结构特征的基础上进行解题定向，首先确定解题方向和解题思路，再进行具体的计算或推理。也就是让学生形成解决问题时先寻找思路，在思路接通后再进行具体的推理或运算的良好习惯；摒弃拿到题目就动笔、写到哪里算哪里、做不下去再涂改的不良习惯。在问题解决后，对问题解决的方法进行评价、反思、概括，从问题解决的过程中提炼出数学思想方法和解决问题的策略。

综上，数学教师一定要用好作业讲评这一师生交流的平台，要让学生在讲评中纠正错误、规范表达、交流互动、巩固知识、总结规律、掌握方法，提高数学思维品质，使学生能够真正地有所发现，有所感悟，有所提高。这样，数学作业讲评才能发挥出其应有的教学功效。