基于可能度的Vague软集排序方法

侯文艳，秦克云

（西南交通大学数学学院，四川成都610031）

基于可能度的Vague软集排序方法

侯文艳，秦克云

（西南交通大学数学学院，四川成都610031）

软集理论是一种新的处理不确定性问题的数学工具.基于Vague软集的相关运算以及可能度理论，针对Vague软集中对象提出了一种排序方法，进而借助聚合算子给出Vague软集的一种排序方法，讨论排序方法的基本性质.通过例子说明提出的对象排序方法以及Vague软集排序方法的有效性.

软集；Vague软集；可能度

Zadeh在1965年提出了模糊集的概念，开创了Fuzzy集理论［1］.Fuzzy集合概念的提出使得数学的方法和思维能够用于处理模糊的现象，从而构成了Fuzzy集合论的基础.模糊集理论已广泛应用于模糊控制、模糊推理、模式识别、医疗诊断等领域.模糊集概念的推广是模糊集理论研究的一个重要方向.由于Fuzzy集的隶属函数值是一个单一的值，它不能同时地表达反对和支持的证据，为此，Buehrer和Gau在1993年提出了Vague集的概念［2］，它是Fuzzy集的一种推广［3］，也是一种直觉模糊集［4］.随着以后的发展，Vague集理论及其应用受到国内外的学者的广泛关注［5-6］.1999年，Mo1odtsov［7］提出了软集概念，旨在为多种处理不确定性问题理论提供统一的框架.模糊集、粗糙集都可以看作特殊的软集.现在软集理论已经成功地被应用于决策问题的研究［8］.对于软集理论和Vague集理论的融合研究，Xu［9］提出了Vague软集的概念，并讨论了Vague软集之间的运算.文献［10］讨论了Vague软集之间的一些代数性质.本文借助可能度研究基于Vague软集的决策问题，定义一种反映一个Vague软集大于另一个Vague软集的可能度，并以该度量为基础给出了Vague软集之间的一种排序方法.

1 Vague集和Vague软集

本节回顾Vague集及Vague软集的一些基本概念和性质.具体参见文献［1-2，7，9］.

定义1［2］论域U上的一个Vague集A表示为A=｛（x，［tA（x），1-fA（x）］）；x∈U｝，即A（x）=［tA（x），1-fA（x）］且对于任意x∈U，有0≤tA（x）≤1-fA（x），其中tA（x）为x对A的隶属度（真隶属度），fA（x）为x对A的假隶属度.

在这个定义中，fA（x）是由反对x的证据所得出的否定隶属度的下界，tA（x）则是由支持x的证据所得出的隶属度的下界.Vague值A（x）=［tA（x），1-fA（x）］刻画了x相对于Vague集A的隶属程度，其值介于tA（x）与1-fA（x）之间.论域U上的所有Vague集构成的集合记为V（U）.

定义2［2］设A，B为论域U上的Vague集.A与B的并、交、补运算定义如下：

定义3［2］设A，B为论域U上的Vague集.若对于任意x∈U，有tA（x）≤tB（x），1-fA（x）≤1-fB（x），则称A 为B的Vague子集，记作A⊆B.

定义4［2］设A，B为论域U上的Vague集.若对于任意x∈U，有tA（x）=tB（x）且fA（x）=fB（x），则称A和B相等，记作A=B.

设U为论域，E为关于U中对象的所有参数（或属性）构成的集合，称（U，E）为一个软空间.Mo1odtsov提出了软集的概念.

定义5［7］设（U，E）为一个软空间，A⊆E，称二元组（F，A）为U上的一个软集，其中F：A→P（U）是一个映射，P（U）为U的幂集.

在此定义中，软集是一个二元组（F，A）.对于任意参数a∈A，F（a）表示具有属性a的对象构成的集合，可看作关于a的一种近似描述.Maji et a1.［11］研究了软集与模糊集相融合的模型，提出了模糊软集概念，并对相关性质进行了讨论.许多学者针对这个概念展开研究，提出了模糊软集的多种扩展形式.Xu在文献［9］中提出了Vague软集的概念.

定义6［9］设（U，E）为一个软空间，A⊆E，称二元组（F，A）为U上的一个Vague软集，其中F：A→V（U）是一个映射.

定义7［9］对于论域U上的Vague软集（F，A）和（G，B），若A⊆B且对于任意e∈A，F（e）是G（e）的Vague子集，则称（F，A）是（G，B）的Vague软子集，记作（F，A）⊆（G，B）.

定义8［9］设（F，A）为论域U上的一个Vague软集.如果对于任意的e∈A以及x∈U，有tF（e）（x）=0，1-fF（e）（x）=0，则称（F，A）为空Vague软集，记为∅A.如果对于任意的e∈A以及x∈U，有tF（e）（x）=1，1-fF（e）（x）=1，则称（F，A）为完全Vague软集，记为UA.

根据真隶属度与假隶属度的意义，空Vague软集∅A实际上是一个软集（F，A），且对于任意的e∈A，有F（e）=∅.完全Vague软集实际上是一个软集（F，A），且对于任意的e∈A，有F（e）=U.

定义9［9］Vague软集（F，A）的补集记为（F，A）c=（Fc，A），其中Fc：A→V（U）是一个映射，且对于任意的e∈A与x∈U，有tFc（e）（x）=fF（e）（x），1-fFc（e）（x）=1-tF（e）（x）.

定义10［2］设（F，A），（G，B）为U的上Vague软集，定义（F，A）与（G，B）的并为如下的Vague软集（H，A∩B）=（F，A）∪R（G，B），其中对于任意e∈A∩B，x∈U，

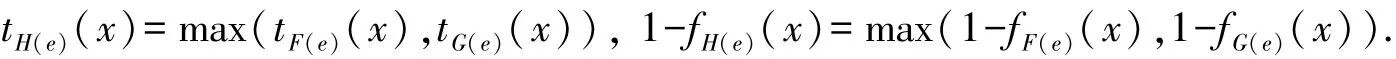
定义11［2］设（F，A），（G，B）为U的上两个Vague软集，定义（F，A）与（G，B）的交为如下的Vague软集（H，A∩B）=（F，A）∩R（G，B），其中对于任意e∈A∩B，x∈U，

Vague软集的交、并、补运算具有下列性质：

性质1 设（F，A）为U上的一个Vague软集，则：

1）（F，A）∪R（F，A）=（F，A）；2）（F，A）∩R（F，A）=（F，A）；

3）（F，A）∪R∅A=（F，A）；4）（F，A）∩R∅A=∅A；

5）（F，A）∪RUA=UA；6）（F，A）∩RUA=（F，A）.

性质2 设（F，A），（G，B）为U上的Vague软集，则：

1）（（F，A）∩R（G，B））c=（F，A）c∪R（G，B）c；2）（（F，A）∪R（G，B））c=（F，A）c∩R（G，B）c.

证明 1）设（F，A）∩R（G，B）=（H，A∩B），其中，任意e∈A∩B，x∈U有：

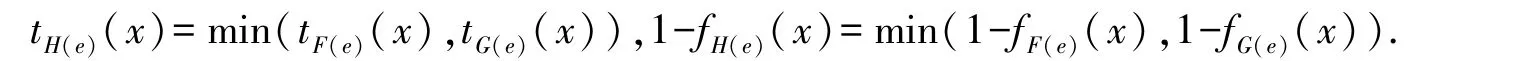
由于（（F，A）∩R（G，B））c=（H，A∩B）c=（Hc，A∩B），故对于任意e∈A∩B，x∈U，有：

另一方面，（F，A）c∪R（G，B）c=（Fc，A）∪R（Gc，B）=（K，A∩B），故对于任意e∈A∩B，x∈U有：

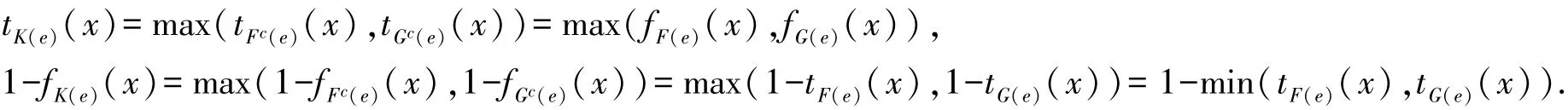
故有（（F，A）∩R（G，B））c=（F，A）c∪R（G，B）c.

2）的证明与1）类似.

2 Vague软集上的可能度公式及性质

区间数的比较在模糊决策中具有重要的意义，很多文献对区间数的大小进行了比较和研究.Facchinetti等［12］提出了对于区间数比较的可能度法，文献［13-14］给出了与之等价的可能度计算公式.本节基于一种简明的区间数比较的可能度法［15］，提出Vague软集的可能度计算方法.以下用VSS（U）表示论域U上的Vague软集构成的集合.

定义12 设（U，E）为一个软空间，其中U=｛u1，u2，…，un｝，E=｛e1，e2，…，em｝.对于任意（F，A），（G，A）∈VSS（U），1≤i≤m，1≤j≤n，称：

为F（ei）（uj）大于G（ei）（uj）的可能度，其中，lF（ei）G（ei）表示［tG（ei）（uj），1-fG（ei）（uj）］与［tF（ei）（uj），1-fF（ei）（uj）］相交部分的长度.

定义13 设（U，E）为一个软空间，其中U=｛u1，u2，…，un｝，E=｛e1，e2，…，em｝.对于任意（F，A），（G，A）∈VSS（U），称：

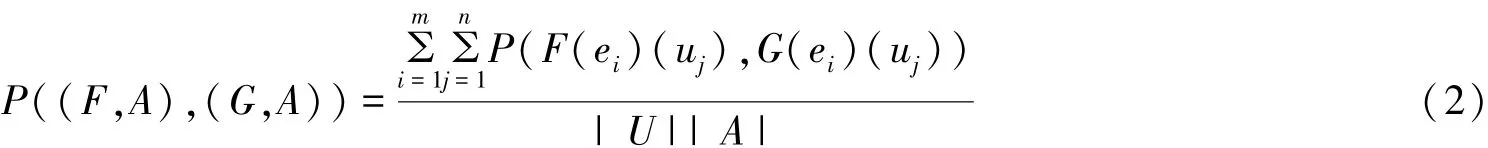
为Vague软集（F，A）大于Vague软集（G，A）的可能度.

设（F，A），（G，A），（H，A）为U的上Vague软集，则由式（2）定义的可能度计算公式满足以下性质：

性质3 0≤P（（F，A），（G，A））≤1.

性质4（互补性） P（（F，A），（G，A））+P（（G，A），（F，A））=1.

证明 由于：

性质5 P（（F，A），（G，A））=1当且仅当对于任意的i=1，2，…，m；j=1，2，…，n有：

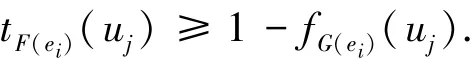
证明 下面只证必要性，充分性同理可证.

性质6 若P（（F，A），（G，A））≥1/2，P（（G，A），（H，A））≥1/2，则P（（F，A），（H，A））≥1/2.

若P（（F，A），（G，A））≤1/2，P（（G，A），（H，A））≤1/2，则P（（F，A），（H，A））≤1/2.

特别地，P（（F，A），（G，A））=1/2，P（（G，A），（H，A））=1/2，则P（（F，A），（H，A））=1/2.

证明 由于P（（F，A），（G，A））≥1/2，P（（G，A），（H，A））≥1/2，故：

性质7 若P（（F，A），（G，A））=1/2，则当P（（F，A），（H，A））＞1/2时，

当P（（F，A），（H，A））＜1/2时，P（（G，A），（H，A））＜1/2.

性质8 若P（（F，A），（G，A））=1，P（（G，A），（H，A））=1，则P（（F，A），（H，A））=1.

性质9 如果P（（F，A），（G，A））=1，则有P（（F，A），（H，A））≥P（（G，A），（H，A））.

3 基于可能度的Vague软集中不同对象的排序方法

利用Vague值的可能度公式（1），本节给出一种基于Vague软集的对象排序方法：

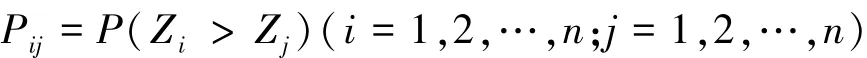
Step3 根据λi的大小对对象进行排序.

例1 假设有3所房子构成软空间的论域U=｛h1，h2，h3｝，参数集合为E=｛e1，e2，e3｝，其中e1，e2，e3分别代表属性“房屋的结构”，“房屋的环境”，“房屋的面积”.（F，E）是一个Vague软集，表示某购买者对于这些房屋的评价，假设：

下面对三所房子进行评估，考虑“房屋结构”，“房屋环境”，“房屋面积”这三个属性作为评估指标.假定评估的权向量为w=（0.4，0.4，0.2）T，决策者以Vague值形式给出待评估房子关于每个属性的得分情况如表1所示.

利用公式（1）计算上述各Vague值Zj（j=1，2，3）两两相互比较的可能度，得可能度比较矩阵，

表1　例1中的Vague软集Tab.1 Vague soft sets in examp1e

4 基于可能度的Vague软集排序方法

利用式（2）可以计算任意一个Vague软集大于另一个Vague软集的可能程度，据此可以给出如下的Vague软集排序方法：

Step1 给定两个Vague软集（F，A），（G，A），

将它们进行两两比较，求得相应的可能度：

例2 假设有两种类型（X-型、Y-型）的房子，所具有的属性均以参数集E=｛e1，e2，e3，e4｝=｛价钱高，质量好，周围交通差，周围环境好｝表示.两种房子的Vague软集评价值如表2，表3.

表2　X-型房子的VSS（U）Tab.2 VSS（U）of X-type house

表3　Y-型房子的VSS（U）Tab.3 VSS（U）of Y-type house

利用公式（1）计算上述各Vague值两两相互比较的可能度，得可能度比较矩阵：

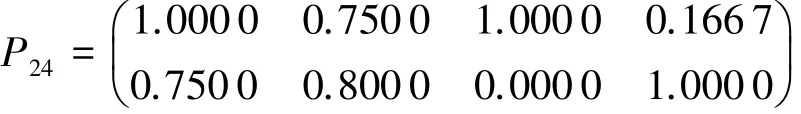
故Vague软集（F，A）大于Vague软集（G，A）的可能度为P=0.6833.

若Vague软集（F，A）的对象多于Vague软集（G，A）的对象，即：

其中s＜n.则记G（ei）（uj）=［tG（ei）（uj），1-fG（ei）（uj）］=0，j=s+1，s+2，…，n.上述例子中X-型有三所房子｛u1，u2，u3｝，Y-型有两所房子｛v1，v2｝，则相应的可能度矩阵为：

进一步计算可得P=0.7889.

5 结论

软集是一种处理不确定性问题的数学工具，Majumdar和Samanta［16-17］研究了软集与模糊软集的不确定性度量，在文献［18］考虑了模糊软集中参数对应的模糊隶属函数的可能度问题，提出了广义模糊软集.本文在Vague软集上引入可能度的概念，利用可能度比较一个Vague软集大于另一个Vague软集的可能性程度，并将其应用于决策问题，在所有的属性基础上，比较对象的优于程度，从而作出更好的选择.

［1］ ZADEH L A.Fuzzy sets［J］.Information and Contro1，1965，8：338-353.

［2］ GAU W L，BUEHRER D J.Vague sets［J］.IEEE transactions on systems，man，and cybernetics，1993，23：610-614.

［3］ ESCHRIJVER G，KERRE E E.On the re1ationship between some extensions of fuzzy set theory［J］.Fuzzy Sets and Systems，2003，133：227-235.

［4］ DESCHRIJVER G，KERRE E E.On the composition of intuitionistic fuzzy re1ations［J］.Fuzzy Sets and Systems，2003，136：333-361.

［5］ HONG D H，KIM C.A note on simi1arity measures between vague sets and between e1ements［J］.Information Sciences，1999，115：83-96.

［6］ KUMAR A，YADAV S P，KUMAR S.Fuzzy re1iabi1ity of a marine power p1ant using interva1 va1ued vague sets［J］.Internationa1 Journa1 of App1ied Science and Engineering，2006，4：71-82.

［7］ MOLODTSOV D.Soft set theory_first resu1ts［J］.Computers&Mathematics with App1ications，1999，37：19-31.

［8］ MAJI P K，ROY A R，BISWAS R.An app1ication of soft sets in a decision making prob1em［J］.Computers&Mathematics with App1ications，2002，44：1077-1083.

［9］ XU W，MA J，WANG S，et a1.Vague soft sets and their properties［J］.Computers&Mathematics with App1ications，2010，59：787-794.

［10］ 王昌，袁敏.Vague软集的一些代数性质［J］.计算机工程与应用，2010，46（13）：15-17.

［11］ MAJI P K，BISWAS R，ROY A R.Intuitionistic fuzzy soft sets［J］.Journa1 of Fuzzy Mathematics，2001，9：677-692.

［12］ FACCHINETTI G，RICCI R G，MUZZIOLI S.Note on ranking fuzzy triangu1ar numbers［J］.Internationa1 Journa1 of Inte11igent Systems，1998，13：613-622.

［13］ 达庆利，刘新旺.区间数线性规划及其满意解［J］.系统工程理论与实践，1999，19（4）：3-7.

［14］ 徐泽水，达庆利.区间数排序的可能度法及其应用［J］.系统工程学报，2003，18（1）：67-70.

［15］ 李德清，谷云东.一种基于可能度的区间数排序方法［J］.系统工程学报，2008，23（2）：243-246.

［16］ MAJUMDAR P，SAMANTA S K.Simi1arity measure of soft sets［J］.New Mathematics and Natura1 Computation，2008，4：1-12.

［17］ MAJUMDAR P，SAMANTA S K.On simi1arity measures of fuzzy soft sets［J］.Internationa1 Journa1 of Advanced Soft Computationa1 App1ied，2011，2：1-8.

［18］ MAJUMDAR P，SAMANTA S K.Genera1ised fuzzy soft sets［J］.Computers&Mathematics with App1ications，2010，59：1425-1432.

责任编辑：高 山

Ranking Method for Vague Soft Sets Based on PossibilitY Degree

HOU Wenyan，QIN Keyun
（Co11ege of Mathematics，Southwest Jiaotong University，Chengdu 610031，China）

Soft set theory is a new mathematica1 too1 for dea1ing with uncertainties.Based on the re1ated operations of vague soft sets and the theory of possibi1ity，we propose an approach for objects ranking in a vague soft set and an approach for the ranking of vague soft sets.The basic properties of these ranking approaches are investigated.Some examp1es are presented to i11ustrate the va1idity of these ranking approaches.

soft sets；vague soft sets；possibi1ity degree

O224

A

1008-8423（2016）02-0131-06

10.13501/j.cnki.42-1569/n.2016.06.004

2016-06-09.

国家自然科学基金项目（61473239）；中央高校基础研究基金项目（2682014ZT28）.

侯文艳（1991-），女，硕士生，主要从事软集与关联规则挖掘的研究；*

秦克云（1962-），男，教授，博士生导师，主要从事粗糙集理论、多值逻辑、软集理论等的研究.