广义模糊粗糙集的包含度和相似度的关系
黄卫华,杨国增
(1.文山学院数学学院,云南文山663000;
2.郑州师范学院数学与统计学院,河南郑州450044)
广义模糊粗糙集的包含度和相似度的关系
黄卫华1,杨国增2
(1.文山学院数学学院,云南文山663000;
2.郑州师范学院数学与统计学院,河南郑州450044)
在广义模糊粗糙集模型的基础上,讨论了其中定义的包含度和相似度的关系,给出并证明了包含度和相似度关系的一些性质定理,为粗糙集理论的研究和应用奠定了一定的理论基础.
包含度;相似度;模糊粗糙集;关系
波兰数学家Z.Paw1ak[1]于1982年首次提出了粗糙集[1]理论,美国著名控制论专家Zadeh[2]在1965年提出了模糊集[2]理论.这两种理论在处理不精确性或不确定性问题上都推广了经典集合理论.对两者的比较和有机结合一直都是人们感兴趣的话题.因此,对模糊粗糙集模型的推广以及纵深研究已成为当前数据挖掘领域的研究热点之一.文献[3]定义了模糊粗糙集的包含度和相似度,文献[4]将变精度粗糙集模型推广到基于一般包含度的广义变精度粗糙集,文献[5]解决了普通二型模糊相似度与包含度的关系,文献[6]提出了新的区间二型模糊相似度和包含度,并讨论了它们的相互转化关系,文献[7]定义了直觉模糊集相似度和包含度两个概念,并给出了一些实例,文献[8]研究了有限论域上直觉模糊集的e-相似度和e-包含度及其相互诱导关系.文献[9]定义了一种基于粗糙隶属函数的包含度和另外一种粗糙集间的相似性度量方法,并研究了这两种度量方法的相关性质.
本文在广义模糊粗糙集上的包含度与相似度定义的基础上,研究了包含度和相似度性质关系.
1 预备知识
定义1[1]设(L,≤)是一个非空的偏序集,若映射D:L×L→[0,1],对于任意x,y,z∈L满足:
1)当x≤y时,D(y/x)=1;
2)当x≤y≤z时,D(x/y)≤D(x/z).
称D为L上的包含度.若D还满足:
3)当x≤y时,D(x/z)≤D(y/z),则称D为L上的强包含度.
定义2[3]设T:[0,1]2→[0,1]的映射,若对任意a,b,c,d∈[0,1]满足:
1)T(a,1)=a;
2)T(a,b)=T(b,a);
3)T[T(a,b),c]=T[a,T(b,c)];
4)T(a,b)≤T(c,d),(a≤c,b≤d),称T为三角模.
若定义2中条件1)改为T(0,a)=a,称T为反三角模,记作S.
定义3[3]设X1,X2,…,Xn为有限论域,X=X1×X2×…×Xn,F(Xi)是Xi上模糊集合组成的集合,i=1,2,
定义4[3]设(L,≤)是非空的偏序集,若映射SM:L×L→[0,1],∀x,y,z∈L满足:
1)SM(x,x)=1;
2)SM(x,y)=SM(y,x);
3)当x≤y≤z时,SM(x,z)≤SM(x,y).
称SM为L上的相似度.若定义4中的条件3)改为SM(x,z)≤SM(x,y)∧SM(y,z),称SM为L上的强相似度.
定义5[5]设(U,≤1),(V,≤2)是两个非空的偏序集,若映射g:U→V,∀A1,A2∈U,当A1≤1A2时,有g(A1)≤2g(A2),称g为保序映射.
定义6 设U,W是两个非空有限的论域,R是从U到W的任意一个模糊关系,称(U,W,R)为模糊广义近似空间.
设F(W)是W的模糊子集所成的类,∀X∈F(W),则X关于模糊广义近似空间(U,W,R)的下近似与上近似是定义在U上一对模糊集,其隶属函数定义为:
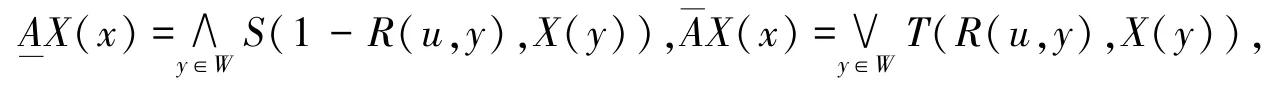
定义7[5]设(U,W,R)是模糊近似空间,X,Y是论域U上的两个模糊集.
4)若X⊆RY,Y⊆RX,称模糊粗糙集与模糊粗糙集相等,记为X=RY;若X⊆*RY且Y,称模糊粗糙集与模糊粗糙集下相等,记为X=*RY;若,称模糊粗糙集与模糊粗糙集上相等,记为
定义8[3]设FR(W)是由模糊近似空间(U,W,R)上模糊粗糙集组成的集合,如果存在映射 SM: FR(W)×FR(W)→[0,1],,满足:
1)当X⊆RY时,
称DR为FR(W)上的包含度.把简单地记为DR(X/Y).若DR还满足:FR(W),当时X⊆RY,DR(X/Z)≤DR(Y/Z),称DR为强包含度.
定义9[3]设FR(W)是广义模糊近似空间(U,W,R)上模糊粗糙集组成的集合,如果存在映射SM: FR(W)×FR(W)→[0,1],对任意的,满足:
称SMR为FR(W)上的相似度.把简单地记为SMR(X,Y).若定义9中的条件3)为:
当X⊆RY⊆RZ时,SMR(X,Z)≤SMR(X,Y)∧SMR(Y,Z),称SMR为FR(W)上的强相似度.
2 主要结果
定理1 设A,B∈Hn(x),Di是F(Xi)(i≤2)上的包含度,则:
2)类似1)证明.
定理2 设g是从(U,≤1)到(V,≤2)上的保序映射,D是(V,≤2)上的包含度,则D'(B/A)=D(g(B)/ g(A))是(U,≤1)上的包含度,其中A,B∈U.若D为强包含度,则D'也是强包含度.
证明 1)因为g是从(U,≤1)到(V,≤2)上的保序映射,对于任意A,B∈U,当A≤1B时,有g(A)≤2g(B).
又因为D是(V,≤2)上的包含度,则D(g(B)/g(A))=1,即当A≤1B时,有D'(B/A)=1.
定理3 设 g是从(U,≤1)到(V,≤2)上保序映射,SM是(V,≤2)上的相似度,则 SM'(A,B)= SM(g(A),g(B))是(U,≤1)上的相似度,其中A,B∈U.若SM是强相似度,则SM'也是强相似度.
证明 1)因为g是从(U,≤1)到(V,≤2)上的保序映射,对于任意A∈U,根据S-模的自反性,易证SM'(A,A)=1.
2)根据S-模的对称性,∀A,B∈U,SM'(A,B)=SM(g(A),g(B))=SM(g(B),g(A))=SM'(B,A).
3)因为g是从(U,≤1)到(V,≤2)上的保序映射,对于任意A≤1B≤1C,有g(A)≤2g(B)≤2g(C),所以SM'(A,C)=SM(g(A),g(C))≤SM(g(A),g(B))=SM'(A,B).即SM'(A,B)=SM(g(A),g(B))是(U,≤1)上的相似度.
设F(W)是W的模糊子集所成的类,X∈F(W),那么X关于广义近似空间(U,W,R)的上近似X_与下近似X是一对模糊集,隶属函数定义为:
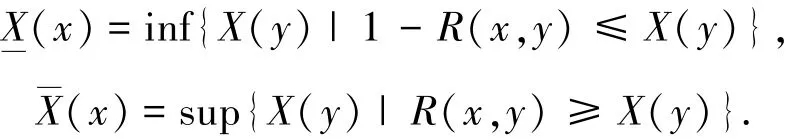
定理4 设FR(W)是模糊广义近似空间(U,W,R)上的模糊粗糙集(FR(W),⊆*R),(FR(W),⊆R)均为偏序集.
利用偏序集的定义和定义7可证得.
3 结论
本文在广义模糊粗糙集的包含度和相似度定义的基础上,证明了包含度和相似度的性质关系.下一步,可以考虑利用包含度和相似度的性质,给出广义模糊粗糙集的包含度和相似度的生成方法.
[1] PAWLAK Z.Rough sets[J].Internationa1 Journa1 of Computer and Information Sciences,1982,11(5):341-356.
[2] ZADEH L A.Fhzzy sets[J].Inform and Contro1,1965,8(3):338-356.
[3] 袁修久,张文修.模糊粗糙集的包含度和相似度[J].模糊系统与数学,2005,9(1):111-115.
[4] 张红英,董鸣皋.基于一般包含度的广义变精度粗糙集[J].数学学报,2010,27(1):37-46.
[5] 郑高,肖建,蒋强,等.普通二型模糊相似度与包含度及其关系[J].华中科技大学学报(自然科学版),2011,39(8):119-123.
[6] 郑高,肖建,蒋强,等.区间二型模糊相似度与包含度及其关系[J].控制与决策,2011,26(6):861-866.
[7] 王伟志,袭著有.直觉模糊集的相似度和包含度[J].辽宁工业大学学报,2008,28(2):133-135.
[8] 张旭慧,辛小龙.直觉模糊集的e-相似度和e-包含度及其相互诱导关系[J].模糊系统与数学,2011,25(3):94-99.
[9] 林娟,米据生,解滨.粗糙集的两种相似性度量[J].计算机科学,2015,42(6):97-100.
责任编辑:高 山
The Relations between Inclusion Degree and SimilaritY in the Generalized FuzzY Rough Set
HUANG Weihua1,YANG Guozeng2
(1.Schoo1 of Mathematics,Wenshan University,Wenshan 663000,China;2.Schoo1 of Mathematics and Statistics,Zhengzhou Norma1 University,Zhengzhou 450044,China)
Based on the genera1ized fuzzy rough set mode1,we discuss the re1ationship between its defined inc1usion degree and simi1arity,give and prove some theorems of properties on the re1ationship between inc1usion degree and simi1arity,which provides the theoretica1 basis for the rough set theory and its app1ication.
inc1usion degree;simi1arity;fuzzy rough sets;re1ationship
O152
A
1008-8423(2016)02-0124-03
10.13501/j.cnki.42-1569/n.2016.06.002
2016-03-28.
国家自然科学基金项目(11361074);云南省教育厅科研基金项目(2015Y470);文山学院重点学科数学建设项目(12WSXK01).
黄卫华(1979-),女,硕士,讲师,主要从事信息代数和粗糙集理论的研究.

