不可约M矩阵最小特征值的界

李艳艳

（文山学院数学学院，云南文山663000）

不可约M矩阵最小特征值的界

李艳艳

（文山学院数学学院，云南文山663000）

利用不可约非负矩阵A和不可约M矩阵B的性质，给出了不可约非负矩阵A。B-1的新上界ρ（A。B-1）≤，以及B的最小特征值τ（B）的新下界数值算例表明了新界的有效性.

不可约；M矩阵；Hadamard积；最小特征值

不可约M矩阵的估计是矩阵分析领域中非常重要的研究课题，近年来受到比较多的青睐，许多学者都对该问题进行过研究，并得到了一系列结果［1-8］.本文在前人的基础上，对该问题继续研究.

为下文的论述，先给出一些定义和引理.

Cn×n（Rn×n）表示n阶复（实）矩阵的集合.A≥0表示所有元素非负的矩阵，并称为非负矩阵，ρ（A）表示A的谱半径.Mn表示非主对角元素非正，逆矩阵元素非负的矩阵的集合，τ（A）表示矩阵A的最小特征值，且有性质.A。B表示阶数相同的矩阵A，B对应元素相乘所得矩阵，称为A和B的Hadamard积.

若A是不可约非负矩阵，那么存在正向量u，v使Au=ρ（A）u，u称为A的右Perron特征向量.

引理1［1］若A是不可约非负矩阵，并且有正向量z，使得Az≤kz，则ρ（A）≤k.

引理2［2］设B=（bij）∈Mn且不可约，y=（yi）是正向量，且使得JBy=ρ（JB）y，则对于有下面的不等式成立：

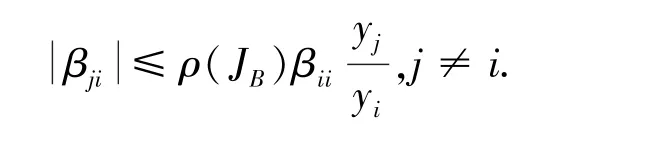
1 主要结论

本部分首先给出不可约M矩阵的逆矩阵主对角元素下界的新估计式，其次利用该新估计式，得到最小特征值的下界.

定理1 设B=（bij）∈Mn且不可约，则对于B-1=（βij）有下面的不等式成立

证明 设D=diag（yi），，因为JBy=ρ（JB）y，则，即，又由引理2知：，且B1B-11=I，则有：

定理2 设A=（aij）是不可约非负矩阵，B=（bij）∈Mn，B-1=（βij），则：

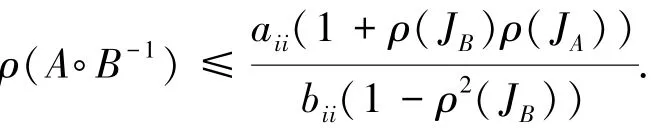
证明 首先假设A，B是不可约的，令JATx=ρ（JAT）x，JBy=ρ（JB）y，其中x=（xi），y=（yi）是正向量，定义z，令C=A。B-1，因为B-1＞0，所以C是非负不可约矩阵.

定理3 设B=（bij）∈Mn，B-1=（βij），则：

证明 在定理2中令A=J，J的每个元素都是1，则ρ（JA）=n-1，并且对于M矩阵B，有

推论1 设B=（bij）∈Mn，B-1=（βij），则：

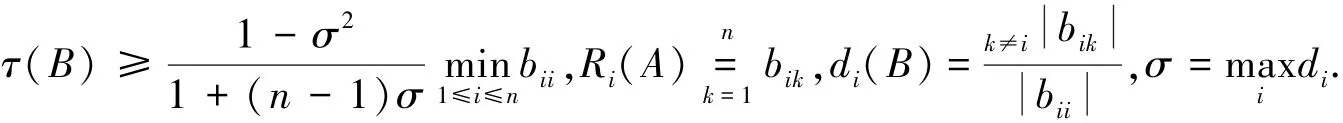
证明 JB=D-1C，D=diag（b11，b22，…，bnn），C=D-B，C是非负矩阵，则，即ρ（JB）≤σ，那么-ρ2（JB）≥-σ2，所以

注1 本文所得估计式的一个最大优点是只与矩阵的元素有关，易于计算.

2 数值算例

得：τ（B）≥0.085，τ（B）≥0.093，事实上真值τ（B）=0.47.通过该例发现，本文所给出的估计式一定情况下，优于现有的结果.所以本文的结论是对M矩阵最小特征值估计的有益补充和进一步完善.

［1］ HORN R A，JOHNSON C R.Matrix Ana1ysis［M］.UK：Cambridge University Press，1985.

［2］ HUNG Rong.Some inequa1ities for the Hadamard product and the Fanproduct of matrices［J］.Linear A1gebra and its App1ications，2008，428：1551 -1559.

［3］ 孙德淑.M矩阵最小特征值的下界新估计［J］.重庆师范大学学报（自然科学版），2016，33（2）：1-6.

［4］ LI C Q，LI Y T，ZHAO R J.New inequa1ities for the minimum eigenva1ue of Mmatrices［J］.Linear and Mu1ti1inear A1gebra，2013，61（9）：1267-1279.

［5］ 王峰.非奇异M矩阵的逆矩阵和M矩阵的Hadamard积的最小特征值下界估计［J］.应用数学学报，2013，36（2）：13-15.

［6］ 赵建兴.M-矩阵最小特征值估计及其相关问题研究［D］.昆明：云南大学，2014.

［7］ 李华，刘玉晓，刘常盛.矩阵Hadamard积最小特征值的新界值估计［J］.重庆师范大学学报（自然科学版），2014，31（6）：54-57.

［8］ TIAN G X，HUANG T Z.Inequa1ities for the minimum eigenva1ue of M matrices［J］.E1ectron J 1inear A1gebra，2010，20：291-302.

责任编辑：时 凌

Bound for the Minimum Eigenvalue of the Irreducible M-matrix

LI Yanyan
（Schoo1 of Mathematics，Wenshan University，Wenshan 663000，China）

In the paper，using the properties of irreducib1e nonnegative matrix A and irreducib1e M matrix B，we give the new upper boundof irreducib1e nonnegative，and the new 1ower boundof the minimum eigenva1ue τ（B）for matrix B.Numerica1 examp1es show the va1idity of the resu1t.

irreducib1e；M matrix；Hadamard product；minimum eigenva1ue

O151.21

A

1008-8423（2016）02-0140-02

10.13501/j.cnki.42-1569/n.2016.06.006

2016-04-08.

云南省教育厅科学研究项目（2013Y585）.

李艳艳（1982-），女，硕士，讲师，主要从事矩阵理论及其应用的研究.