变形Boussinesq方程与Benjamin-Ono方程的可积性与达布变换解
房春梅,薛丽红*,田守富
(1.集宁师范学院数学系,内蒙古乌兰察布012000;2.中国矿业大学理学院,山东徐州221116)
变形Boussinesq方程与Benjamin-Ono方程的可积性与达布变换解
房春梅1,薛丽红1*,田守富2
(1.集宁师范学院数学系,内蒙古乌兰察布012000;2.中国矿业大学理学院,山东徐州221116)
通过引入新的特征值问题首次获得了Benjamin-Ono方程与变形Boussinesq方程的Lax对,并通过函数变换构造了变形Boussinesq方程的达布变换以及此方程与Benjamin-Ono方程的Miura变换,最后通过达布变换与Miura变换获得了这两个方程的若干组精确解.
Benjamin-Ono方程;变形Boussinesq方程;达布变换;Lax对
在非线性科学领域,对于孤子方程的研究显得尤为重要,在过去几十年的时间里,人们已经研究出许多构造孤子方程精确解的方法[1-4],主要有Back1und变换法、反散射方法、hirota双线性方法、ck直接法、Darboux变换方法等等.其中,Darboux变换法已经成功地求解了一系列与特征值问题相关联的孤子方程.
本文主要考虑Benjamin-Ono方程:

文献[5-7]已对该方程做了一系列的研究,获得了该方程的Back1und变换与精确解.
本文的具体工作如下:
先引入一个特征值问题导出了一个新的变形Boussinesq方程,
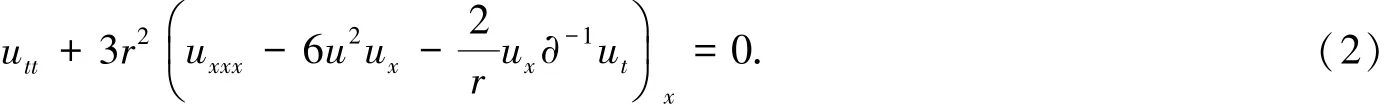
并获得了此方程的Lax对与达布变换.同样引入一个特征值问题导出了Benjamin-Ono方程,以及此方程与变形Boussinesq方程的Miura变换;最后通过达布变换与Miura变换获得了变形Boussinesq方程的与Benjamin-Ono方程的若干组精确解.
1 变形Boussinesq方程的Lax对与达布变换
引入一个特征值问题:
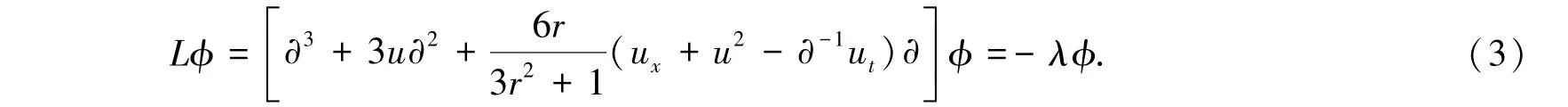
对应于(3)的特征函数的时间演化为:

那么,通过直接计算可以得到下面的命题:
定理1 假定ϕ满足式(3)和式(4),则Lt=[B,L]就是变形Boussinesq方程(2).
对于定理1可直接通过计算验证.
命题1 假定当λ=λ0时,f满足式(3)和式(4)且具有如下形式,
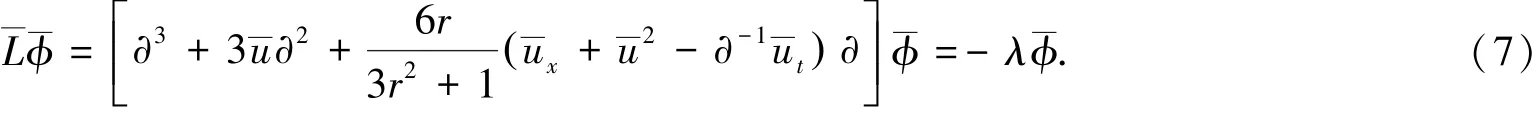
证明 当λ=λ0时,f满足:

命题2 假定当λ=λ0时,f满足式(3)和式(4)且具有式(5)与式(6)形式,则ϕ_满足:

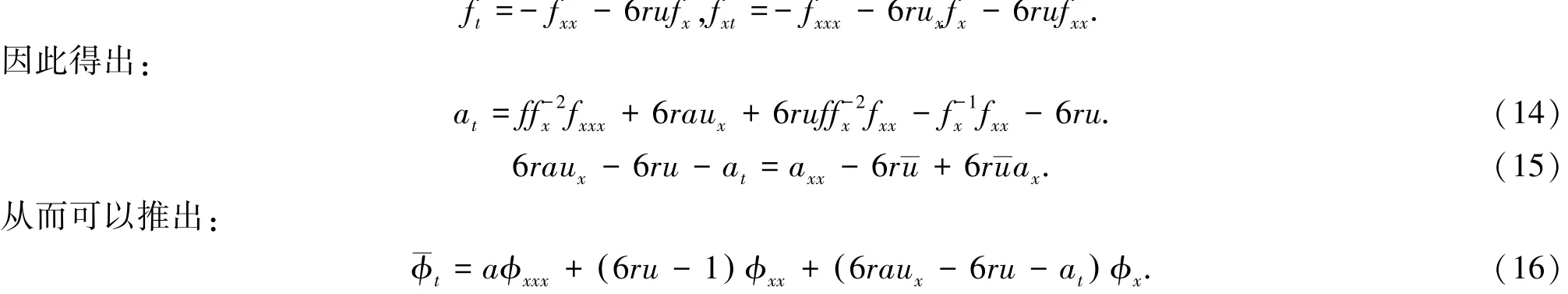
从式(14)~(16)即可推出式(13)成立.
命题1,2说明了变换式(5)、(6)将Lax对式(3)、(4)变成具有完全相同形式的Lax对式(7)、(13).由定理1可知,两个Lax对对应的是同一方程(2).称为变形Boussinesq方程(2)的一个达布变换[8-9].综上,可得出下面的定理:
定理2 变形Boussinesq方程(2)的解u在变换式(5)、(6)下变成一个新解.
2 Benjamin-Ono方程的Lax对以及与变形Boussinesq方程的Miura变换
引入两个算子L1,B1如下:
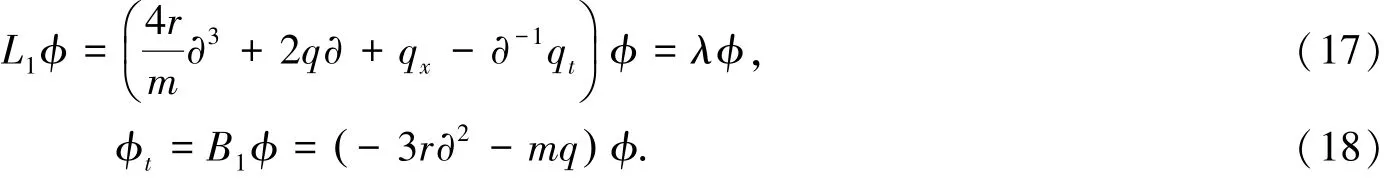
通过直接计算L1,t=[B1,L1]就能得到Benjamin-Ono方程(1).所以方程(1)在Lax意义下是可积的.算子L1,B1称为Benjamin-Ono方程(1)的Lax对.
假定u=ϕxϕ-1,则容易得出式(17)、(18)两式能改写成如下形式:
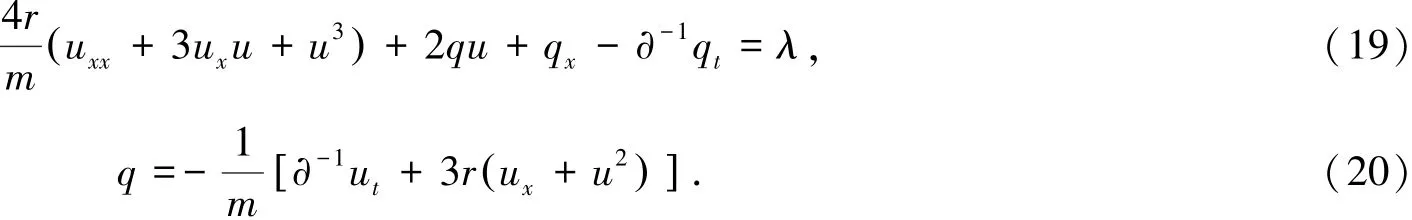
将式(19)关于时间t求导,再将上几式带入得到:
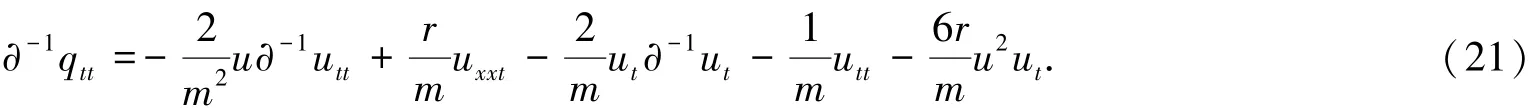
由式(20)可以计算出:

从而可得出Benjamin-Ono方程与变形Boussinesq方程之间的Miura变换.
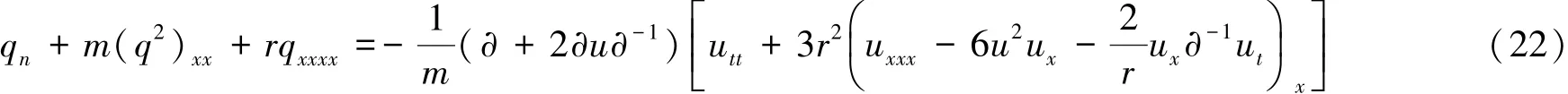
经过以上分析,能得出以下定理:
定理3 假定u是变形Boussinesq方程的解,那么在变换(20)下所得解是Benjamin-Ono方程的解.
称变换(20)为Benjamin-Ono方程与变形Boussinesq方程之间的Miura变换.
3 变形Boussinesq方程与Benjamin-Ono方程的精确解
本节通过达布变换(6)与Miura变换(20)给出变形Boussinesq方程与Benjamin-Ono方程的若干种精确解.
假定取u=b(常数)为变形Boussinesq方程的种子解,且λ=λ0,则式(3)、(4)变为:

下面分三种情况进行求解:
情况1 当b=0,λ0=0,时可以得出方程组(23)~(24)有如下解:

其中ci(i=0,1,2)是常数,且由Darboux变换式(6)得出式(2)的解为:
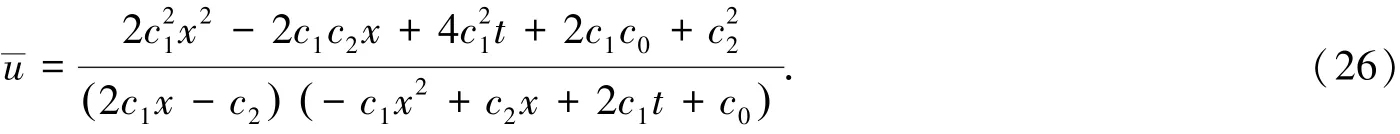

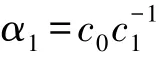
2)当时,由式(26)化简可得奇点解:
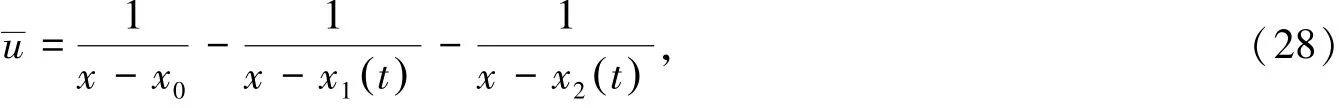
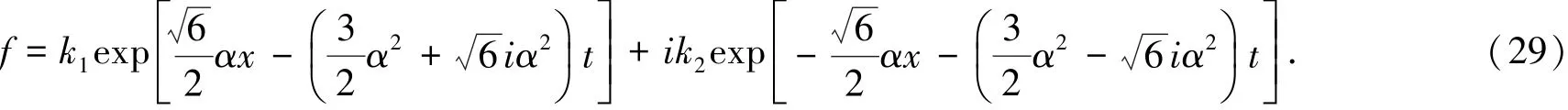
由达布变换式(6)得出方程(2)的孤子解:
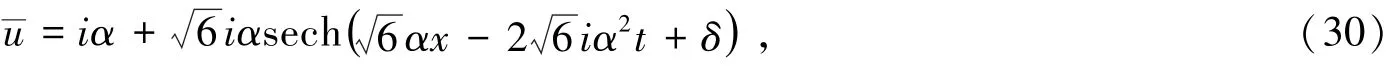
情况3 设b=0,λ0=-β3,则可以得出方程组(23)~(24)有如下解:
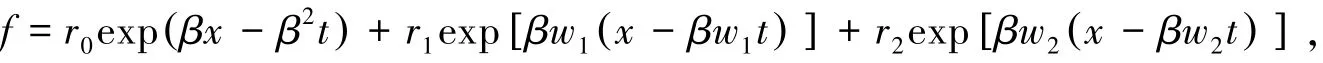
1)当r0=0,由达布变换式(6)得出方程(2)的周期解:
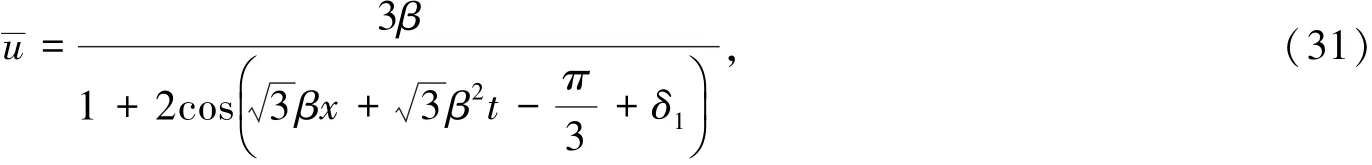
2)当r2=0,由达布变换式(6)得出方程(2)的解:
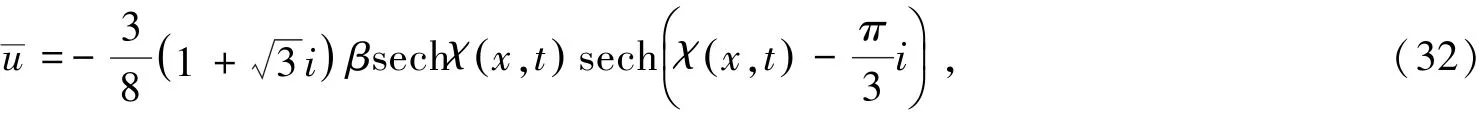
最后由Benjamin-Ono方程与变形Boussinesq方程之间的Miura变换(20)可以得到与上面变形Boussinesq方程的解对应的Benjamin-Ono方程的几组精确解.
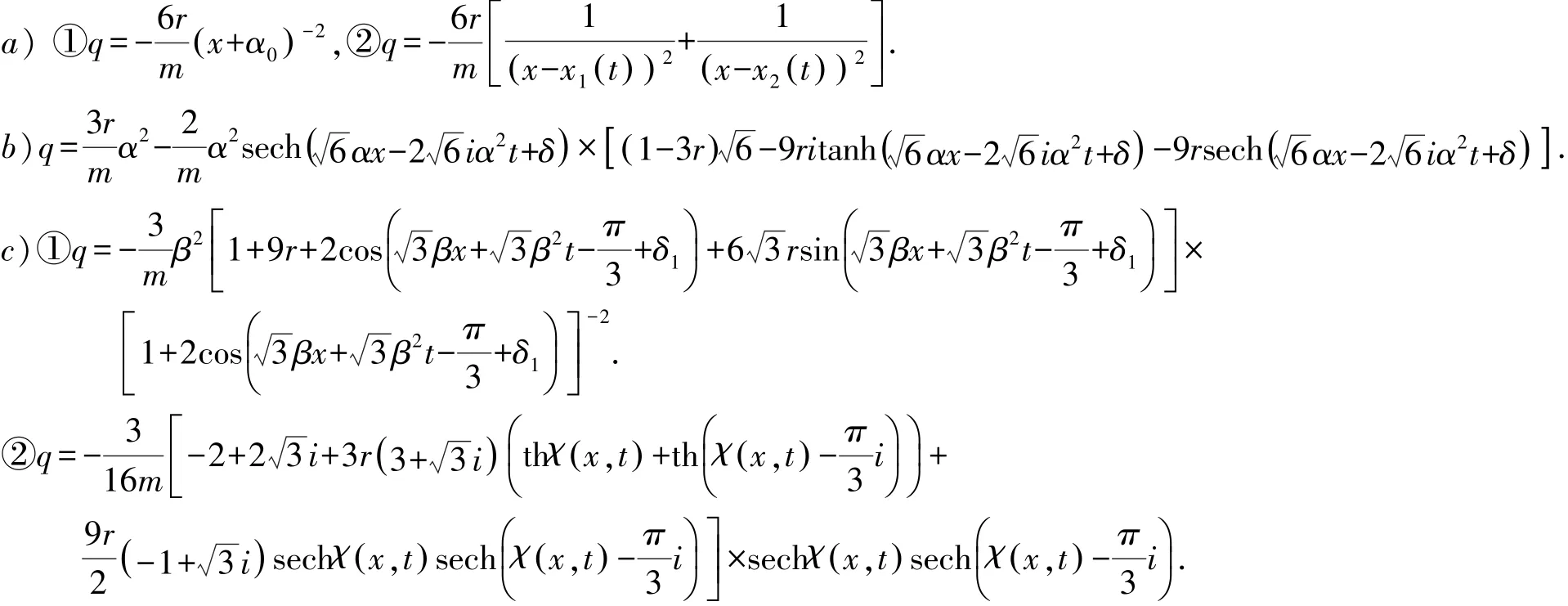
[1] 耿献国.变形Boussinesq方程的Lax对和Darboux变换解[J].应用数学学报,1988,11(3):324-328.
[2] 沈守枫,于水猛,李春霞,等.2n维空间中的广义自对偶Yang-Mi11s方程的达布变换[J].数学物理学报,2015,35A(3):478-486.
[3] ZHA Qi1a.A Negative Order Genera1ized WKI Hierarchy,Bi-Hami1tonian Structure,and Da rboux Transformation[J].Journa1 of Mongo1ia Norma1 University,2014,43(5):529-534.
[4] HIROTA R.The Direct Method in So1iton Theory[M].Cambridge:Cambridge University Press,2004.
[5] 张鸿庆,张玉峰.Benjamin方程的Back1und变换、非线性叠加公式及无穷守恒律[J].应用数学和力学,2001,22(10):1017-1021.
[6] WANG Zhen,ZHANG Hongqing.A method for constructing exact so1utions and app1ication to Benjamin Ono equation[J].Chinese Physics,2005,14:2158-2163.
[7] 非线性长波方程组和Benjamin方程的新精确孤波解[J].物理学报,2006,55(7):3246-3254.
[8] ZHA Qi1ao.N-so1iton so1utions of an integrab1e equation studied by Qiao[J].Chinese phys B,2013,040201-1-040201-6.
[9] ZHA Qi1ao,LI Zhibin.Periodic-so1iton so1utions of the(2+1)dimensiona1 kadomteev-Petviashvi1i equation[J].Chinese phys B,2008,17(7):2333-2338.
责任编辑:高 山
The IntegrabilitY and Darboux Transformation Solutions for the Benjamin-Ono Equation and the Modified Boussinesq Equation
FANG Chunmei1,XUE Lihong1*,TIAN Shoufu2
(1.Department of Mathematics,Jining Norma1 University,Wu1anchabu 012000,China;2.Department of Mathematics,China University of Mining and Techno1ogy,Xuzhou 221116,China)
In this paper,based on the new eigenva1ue prob1em,we first get the 1ax pair of Benjamin-Ono equation and the modified Boussinesq equation.With the he1p of function transformation,the Darboux transformation of the modified Boussinesq equation is constructed.The Miura transformation of Benjamin-Ono equation and the modified Boussinesq equation is obtained.Fina11y,some so1utions of the two equations are derived via the resu1ting Darboux transformation and Miura transformation.
Benjamin-Ono equation;modified Boussinesq equation;Darboux transformation;Lax pair
O175.29
A
1008-8423(2016)02-0127-04
10.13501/j.cnki.42-1569/n.2016.06.003
2016-04-17.
国家自然科学青年基金项目(11301527);2015年集宁师范学院科学研究项目(jsky2015028).
基金项目:房春梅(1985-),女(蒙古族),硕士,讲师,主要从事孤立子与可积系统的研究;*通信作者:薛丽红(1981-),女(满族),硕士,讲师,主要从事最优化理论与应用的研究.

