量子信息单调性的研究
向玉玲,严 倩
(重庆师范大学数学科学学院,重庆401331)
量子信息单调性的研究
向玉玲,严 倩
(重庆师范大学数学科学学院,重庆401331)
阐述的是当ρ为3维复Hi1bert空间中不相干的密度算子时,Skew information单调递减,且在2维的量子体系中Skew information是单调递减的启发下继续讨论其单调性.
单调性;密度矩阵;换位子;迹
Skew information由Wigner-Yanase首次提出,已有50多年的发展历史了.该信息在数学及量子力学方面之所以成为许多学者研究的重要课题,是因为以下三点:
1)Skew information与不确定度关系有着密切的联系,如:Heisenberg型不确定关系,其中它们是通过迹不等式联系的,也可以用来检验量子纠缠.
2)Skew information在2-量子态系统里要考虑一些非线性迭代模型的衰退原理,说明该信息与一致连续的熵态是等价的.
3)Skew information在不相干的算子下可能是单调递减的[1],研究该信息单调性是对量子力学在讨论系统信息的遗失问题会给出很好的帮助.
1 预备知识
在1963年Wigner和Yanase[2]首次提出量:

则称其为Skew information,其中tr表示迹(trace),[]表示换位子,即:A,B[]=AB-BA,ρ为密度算子,H为Hami1tionian算子.
定义1[3]ρ为密度算子,

为另一个密度算子;则有:

{ρj}为一列密度算子,则有:

定义2[4]仿射变换:,其中ρ,σ是密度算子.
引理1[5]量子信息(Skew information):有以下三条性质:
ii)量子信息在张量积下满足可加性:
iii)若ρt满足Landau-Von Neumann等式,从而∀t∈ℝ有:),则称:
量子信息满足不变性.
引理2[3]等式成立的充要条件是:与H相交换.并且有:
ii)当H为2阶Hermite矩阵时,则:不等式(4)成立.
引理3[6]设仿射变换是密度算子,则:
引理4[6]设ρ,σ为复合系统H1⊗H2的密度算子,并令ρ1=tr2ρ,ρ2=tr1ρ分别为ρ在H2,H1上的部分迹,σ1=tr2σ,σ2=tr1σ也分别为σ在H2,H1上的部分迹,则:

2 主要结论
定理1 若对为Hi1bert空间H上所有密度算子组成的集合),满足:,其中U为酉算子,τ为密度算子,tra为部分迹,则:

由引理4[4]可得:有:
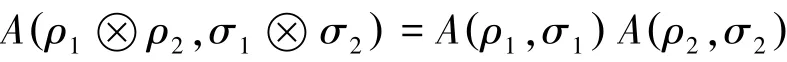
则有:
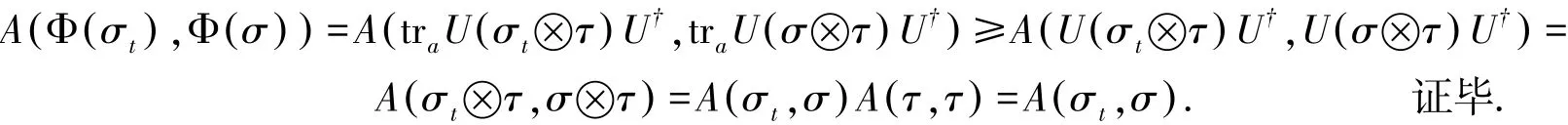
定理2 设引理2中i)成立,则:当H为三阶Hermite矩阵时,不等式(4)成立.
且对密度矩阵ρ为:
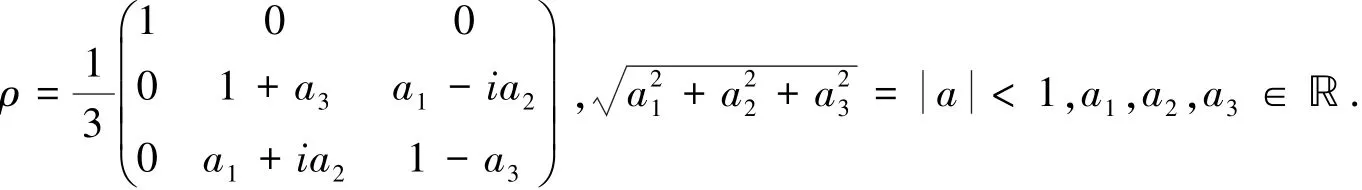
由于ρ是密度算子,则ρ必为正定的Hermite矩阵,一定存在矩阵,则可以计算出:
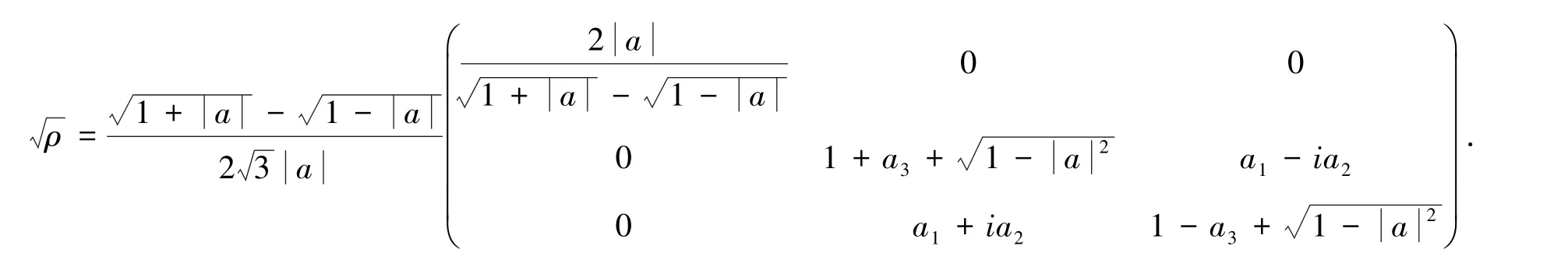

下面给出一个例子,满足不等式(3)严格成立,则不等式(4)也是成立的.
例1 对λ1+λ2+λ3=1,λj>0,令:
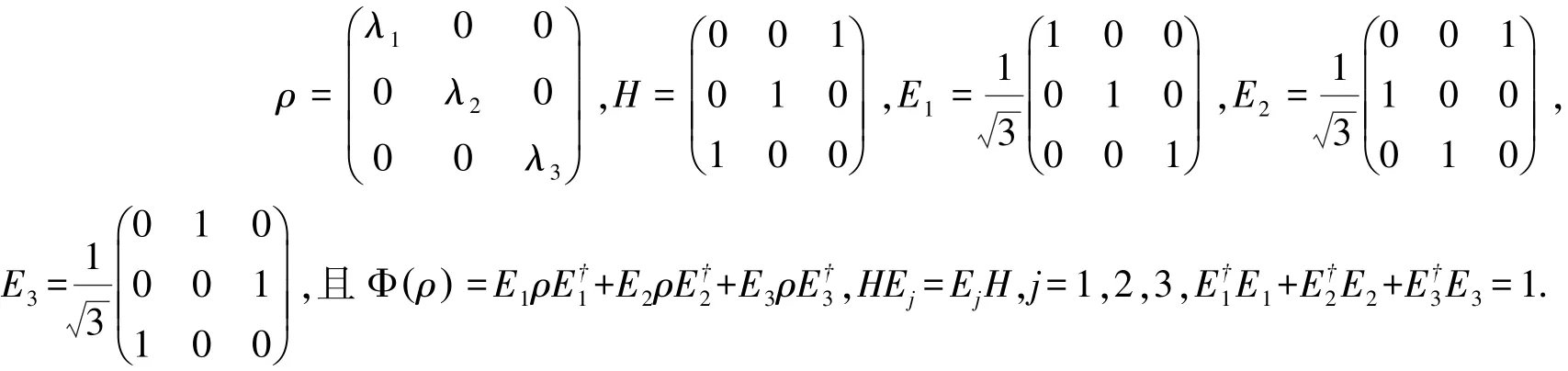
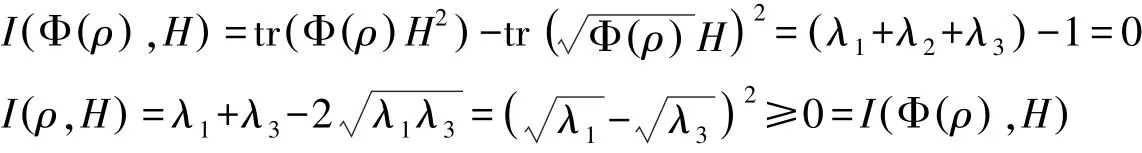
故不等式(3)成立.
3 小结
本文主要说明在3维复Hi1bert中Skew information是单调递减的,实际上,该结论对后续研究Skew information在一般的空间中的单调性有一定的理论基础.
[1] DU S P,BAI Z F.The Wigner-Yanase information can increase under phase sensitive incoherent operations[J].Anna1s of Physics,2015,359:136 -140.
[2] WIGNER E P,yANASE M Y.Information contents of distribution[J].Proceedings of the nationa1 academy of sciences of the united states of America,1963,49:910-918.
[3] LUO S L,ZHANG Q.Skew information decreases under quantum measurements[J].Theoretica1 and Mathematica1 Physics,2007,151(1):529-538.
[4] CHEN Z Q.Wigner-Yanase skew information as tests for quantum entang1ement[J].Physica1 Review,2005,A 71,052320.1-052320.5.
[5] LUO S L,ZHANG Q.On skew information[J].IEEE transaction on information theory,2004,50(8):1778-1782.
[6] LUO S L,ZHANG Q.Information distance on quantum-state space[J].Physica1 Review,2004,69(3):032106.1-032106.8.
责任编辑:时 凌
Research on MonotonicitY of Quantum Information
XINAG Yu1ing,YAN Qian
(Schoo1 of Mathematics,Chongqing Norma1 University,Chongqing 401331,China)
In this paper,we propose skew information can decrease under a c1ass of incoherent operations in the three-dimensiona1 Hi1bert space.And it is fo11owing the framework of skew information decrease under non-se1ective quantum measurement for two-dimensiona1 quantum systems.
monotonicity;density operator;commutator;trace
O177
A
1008-8423(2016)02-0142-04
10.13501/j.cnki.42-1569/n.2016.06.007
2016-04-19.
国家自然科学基金面上项目(11271390).
向玉玲(1990-),女,硕士生,主要从事泛函分析的研究.

