初中聋生学习图形与几何的特点及教学对策研究

吴光安

（厦门市特殊教育学校福建厦门361008）



初中聋生学习图形与几何的特点及教学对策研究

吴光安

（厦门市特殊教育学校福建厦门361008）

图形与几何是初中数学重要内容，但聋生由于生理缺陷等原因，在学习的过程中遇到了不少困难.教师应该从学习习惯、兴趣、学习方法等学生学的角度以及教师教的角度入手做好聋校的图形与几何的教学，帮助聋人尽量学好图形与几何。

初中聋生；图形与几何；教学策略

一、问题的提出

图形与几何是初中数学重要的教学内容，它具有很好的育人价值，对于培养青少年形成良好的空间能力和严密的逻辑思维能力等方面，具有重要的促进作用。我校的聋生从八年级开始学习较为系统的几何知识（使用普通学校人教版七年级的教材），开始接触不少定理，并学习几何证明。在教学过程中，笔者发现聋生学习几何的情况是不尽如人意的。具体表现在以下几个方面：

（一）所掌握的知识基础很薄弱。小学阶段有关几何的主要内容有：三角形的内角和、三角形的分类、正方形、长方形、平行四边形、三角形、梯形和圆的周长和面积公式，等等。这些内容对于普通学校大部分学生来说，是很简单，但聋人却掌握得不够好，比如就三角形的面积公式提问八年级平时学习成绩比较好的同学，他们居然说不出，或说错了。

（二）学习习惯不好。比如很多学生竟没有常用的学习用品（圆规、三角尺等）。上课的时候连课本都不放在桌上，至于课堂练习本，直到老师提醒了，找了好久才找到。不少学生虽然能按时交作业，但学生收到老师批改后的作业后，没有及时地看看自己的作业是否做对了，就算发现做错了，也不想着要订正，即被动学习的现象比较严重。

（三）理解文字能力差。比如让学生根据题目的意思画图点在直线上”，学生理解成“点在直线的上面”。

（四）读图能力不强。比如，学习了角的概念，就交于一点的三条射线所形成的角的个数问题问学生，学生回答2个，少了一个，不能用整体的眼光地看问题，可见学生思维流于表征而缺乏深刻性[1]，只是用眼睛看世界，没有抓住事物的本质特征。

二、原因分析与教学策略

出现上述的种种问题，原因是很正常的。聋生初学几何要比初学代数困难得多，代数虽然比算术抽象，但仍旧是对数和式的运算，学生初学时困难小些。几何主要不是对数和式运算，而是运用几何语言、作图等进行演绎推理，对几何图形的性质进行证明，这对初学几何的学生来说是抽象的，很不习惯。但是聋人教育专家在实验中得出“聋人表现了不显著的左视野——右脑优势，听力正常的人表现了不显著的右视野——左脑优势”[2]。根据这一理论，聋生是完全有能力学好数学的，一个人学习成绩的好坏，一般与这个人的学习基础、习惯、兴趣和方法等有关系。笔者在教学实践过程中，对上述几个因素做了些研究，总结出以下经验。

（一）从学生“学”的角度看。

1.注意聋生非智力因素的培养。

（1）让学生有信心学好数学。培养学生树立“聋人除了听，什么事都能做”的信念。社会学习论的主要提出者班杜拉指出：人的行为的获得，是由学习者在社会情境中，经观察别人行为表现的方式以及行为后果间接获得的[3]。可以给学生例举成功聋人的事迹，比如，让学生知道贝多芬在耳聋的情况下，仍能创作出美妙的音乐；又如，号召学生向身边杰出的聋人学习学习，近年来，我校每年都有一些学生考上长春大学等高校，笔者请学生思考“他们都能考出好成绩，为什么我就不能呢？”以激励他们学习的信心与斗志；比如，给学生讲关于“85后聋女（刘轶，华中师范大学特殊教育专业研究生）考取美4所高校博士，读唇考过六级听力”[4]的故事，以此激发聋人树立更大的梦想，进而有更强的学习动力。

（2）培养学生养成良好的学习习惯。“好习惯使人终生受益”。教育学生要知道作为一个学生要准备好诸如圆规、直尺等常用的学具；还有课前一定要预习；上课前要把课本、练习本、学具和笔等准备好放桌上；不懂就要勤思考，如果想不出就要问老师或者同学，养成勤学好问的好习惯。

（3）激发学生学习几何的兴趣。兴趣是引发学习动机的重要因素，教学中要始终注意激发学生积极主动学习的内部诱因[5]。可以让学生动手解决有一定趣味性的与几何知识有联系的问题，例如，请以给定的图形“○○、△△、=”(两个圆、两个三角形、两条平行线段)为构件，构思尽可能多而独特且有意义的图形[6]。通过这个数学活动，学生想象的翅膀打开了，设计了许多有趣的图形，同学们看着自己设计的作品，心里荡漾着学习几何的喜悦。还可以设计一些会产生视错觉的几何图形让学生观察，使他们在错误的判断与纠错中，体会到学习数学的乐趣，同时认识到学习几何只凭肉眼观察是不可靠的，还要会测量、推理证明。

2.注意夯实学生的学习基础，提高其学习能力。

（1）帮学生把小学的几何基础知识打好。比如，考虑到七年级的聋生对基本图形的相关公式还没掌握好，因此还要向他们讲清楚这些公式的推导过程，由于聋人经常忘记知识，还要在教室的学习园地张贴一些带公式的表格，让学生经常与这些公式见面，从而记住这些基本图形的相关公式。

（2）注重提高聋生思维能力。重点是发散思维的培养。例如，在教同位角、内错角这一节的时候，为了培养学生发散思维能力，笔者问学生两条直线的交点最多有多少个？学生轻松地回答有1个。再问：那三条直线的交点可能有多少个？学生动手实验，学生画出了三种情况，我先和同学们计算出这三种情况的交点个数，后追问学生，还有一种情况被忘记了，请思考，学生有了探究的兴趣，认真思考，但没有发现新的情况，我让学生观察教室，看能不能找到思路，学生从窗户的铁栏那找到思路，画出了互相平行的情形（0个交点）。在这个过程中学生的思维能力提高了，也增加了对几何的兴趣。

（3）通过数学活动提高聋生的几何素养。《义务教育数学课程标准（2011年版）》提出基础知识、基本技能、基本思想和基本活动经验的“四基”教学目标[7]。并特别强调数学活动经验的积累是提高学生数学素养的重要标志。因此教师要多设计一些数学活动，来提高聋生对几何的感觉。比如，让学生玩七巧板拼图，从中感受“等积”的意义；在折纸的过程中，体会图形的对称等性质；通过摆拼三根木条看是否能构成三角形，认识三角形的三边关系等等。在数学活动中积累了丰富的数学活动经验，这种经验只是教学活动的起点，还需要学生在自主探究、教师指导以及同学交流等过程中把握其数学知识本质，反思、抽象、概括，从而内化为学生自身认识数学知识结构的一部分[8]。

（4）注意聋生观察图形能力的训练[5]。一个是作图，一个是识图。教育学生画图要正确、整洁、美观，养成良好的学习态度和习惯。要注意把概念和图形紧密结合起来，引导学生从图形的本质上去认识图形，而不是从图形的位置上去识别，培养学生思维的深刻性。例如，关于三角形的面积公式，要让学生知道三角形的“底”是相对的，不一定就是所在图形的下边才能为底。聋生由于听力的缺失，他们获得信息的途径主要靠视觉，因此如果学生的观察能力提高了，他们对数学实质的认识一定会更深刻。

(5)重视三种语言能力的培养[5].语言是思维的工具，大量的几何概念、定理都是用特定的数学语言（几何语言）来叙述的，可以说几何教学在很大程度上是几何语言的教学。教师要把“自然语言”、“图形语言”和“符号语言”三者作为联系在一起的一个整体，依次进行分析、讨论，以便学生理解掌握。例如，可以建立如表1的表格的方式来对比学习。通过对比，学生对三种语言的认识更加深刻了，进一步培养了学生的符号意识，发展了学生的数学表达能力[8]。

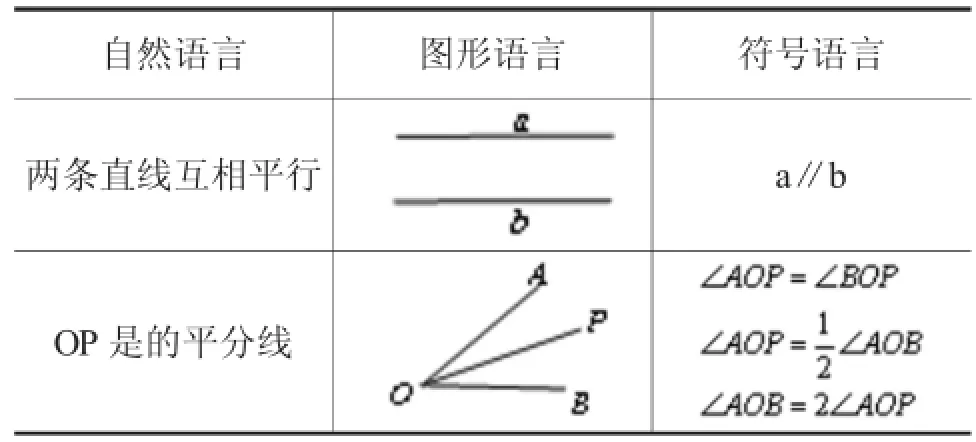
表1　三种数学语言对比

(6)注重证明推理能力的培养。运算和推理是数学活动最重要的两个基本形式[8]。证明推理能力的形成是学习几何的核心，但证明能力的形成不是一两天就可以做到的，它是个长期的过程。在几何教学中要有层次地逐步训练培养学生的推理能力[9]。学生在学习点、线、角等知识的时候，要让学生熟悉几何语言表达定义的特点；在学习平行线的判定与性质的时候，要培养学生具有简单的说理能力，学会用符号“∵、∴”，这个时候的证明比较简单，每一步都要写出推理的理由，避免乱说的坏习惯，这个时候教师还要示范好证明的格式，让学生好模仿。因为聋生不像普通学生，普遍聋人自主学习能力比较差；在学到三角形全等的时候，对学生进一步提高要求，能间接地证明问题。当图比较复杂的时候聋生容易被困扰，因此培养学生能灵活地处理图形是很必要的。例如这题：如图1，点E、F在BC上，BE=CF，AB=DC，∠B=∠C.求证：△ABC≌△DCE。这个图形的两个三角形不是独立的，可以引导学生分别画出和两个三角形（图2），再来分析已知条件与待证之间是什么关系。

图1　

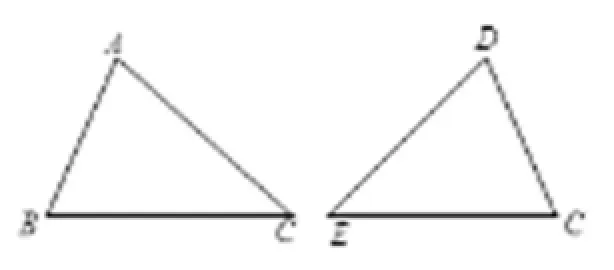
图2　

3.培养聋生掌握一些较好的学习方法。好的方法可以让学习的效率事半功倍。

（1）引导聋生及时地对相关知识进行整理、归纳、对比。通过对比，知识间的同与异在聋生的头脑中就比较清晰。例如，可以建立一表格，将平行线的判定和性质进行对比学习；而涉及某个图形的性质，要及时归纳。通过归纳知识，在解题时才能较快地想到该用哪些知识。比如表2，对直角三角形的知识进行归纳：

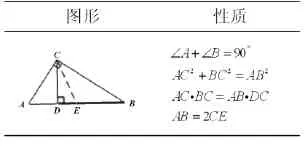
表2　直角三角形性质归纳

（2）形成反思的学习习惯。反思不是反反复复地思考，而是反过来思考。教育学生解答了一道题，如果做对了，要进一步思考是否还有其它方法，是否还有更简单的方法？如果做错了，要分析解题中思路受阻的原因及产生错误后该如何调整思维方式？学生通过反思，掌握探索的方法和解题的规律，培养和发展自我调控能力。

（二）从教师“教”的角度看。

1.多采用直观教学。著名教育家夸美纽斯提出教学直观性原则，并称知识的开端永远是从感官得来的。在教学中，教师应该根据教学内容运用直观手段向学生提供丰富而典型的感性材料，并尽可能地利用恰当的演示或操作使抽象的数学概念转化为具体的内容，让学生通过自己观察、操作与思考等活动逐步建立起清晰的表象，这样就能很好地解决数学概念的抽象性与学生思维形象性之间的矛盾[10]。几何本身很抽象，因此要多使用教具，比如，圆锥、圆柱模型，让学生通过观看模型来记住基本的几何名词及了解它们的基本特征；充分利用两块三角板的价值。它们有45°、30°、60°、90°，问这些角度可以组合成多少种角度呢？学生动手探索，既培养了对角的观察能力，又培养了数感。或从现实中找模型，比如，教室内就有很多几何模型，窗户是长方形，防护网有平行线……

2.注意对教材的取舍。有人说“教什么，远比怎么教重要”。关肇直先生在《从四个现代化看数学教学》中指出：“我们中学数学教育不光是为培养数学家打基础，……，应该着眼于提高全民族的科学文化水平。”[11]因此教材上的内容不必面面俱到到地讲解，而应该有选择性。我们选用的教材是普通学校的教材（人教版初中教材），它的一些内容对于聋人来说太难了，花很多时间下去可能依然讲不清楚，因此有些内容征求教务处同意后，没必要要求学生掌握。比如，一些定理的证明推导过程，定理与逆定理的相关问题，反证法等，可以暂对聋生不做要求。

要充分利用课文的插图。开阔学生的视野，提高学生学习几何的兴趣。比如：课本上有钢结构桥梁、起重机等的插图，笔者让学生欣赏，并思考为什么桥有那么多的三角形呢？学生充分讨论，后在教师的点拨下明白了三角形具有稳定性的特点。

3.用好信息技术。比如在学习《旋转》的时候，我通过几何画板让学生观察图形的旋转过程，让学生对旋转中图形的性质有了更清楚的了解，通过信息技术，让学生欣赏通过旋转可以产生许多美妙的图形（如图3），从而更加热爱学习数学。通过观察几何画板上的不同三角形的内角和，验证三角形内角和的不变性，总是180°。

图3　

4.注意手语表达几何语言的准确性。前面提到聋生理解“点在直线上”时理解成“点在直线的上面”，这种错误多少与教师的手语表达有关系，此处的“上”不是指“上面”，而是指“里面”；又比如，描述物体的路程时说走了一百多里，这个“里”不是“里面”，如果教师打“里面”的手语，学生就会不好理解。关于几何语言用手语来表达的问题，教师要多总结。

5.分层教学，区别对待学生。范希尔理论[12]指出，学生的几何思维有五个水平，层次一：视觉。这个层次水平的儿童能描述几何图形，但无法使用图形的特征或要素名称来分析图形；层次二：分析。例如，学生知道平行四边形有四条边，但不理解它的对边相等；层次三：非形式化演绎。例如，学生了解了等腰三角形的性质后，他们会推出等边三角形也是等腰三角形的一种.层次四：形式演绎。例如，学生能写出一个定理的逆定理.层次五：严密性.在这个层次，学生能在不同的公理系统下严谨地建立定理，以分析比较不同的几何系统，如欧式几何与非欧几何的比较。在教学实践中，可以发现大部分聋生可以达到层次二的水平，较少学生能达到层次四的水平，至于层次五，目前还没有发现哪个中学阶段的聋生能达到。《义务教育数学课程标准（2011年版）》[6]指出“不同的人在数学上得到不同的发展”。因此教师在教学中不要用同一个标准对所有学生，而是多元评价，既要看学生的学业结果，也要看学生的学习过程.对某个学生也不能只停留在某个水平，待时机成熟，就要促其发展。

“加减乘除演绎无限苍穹点线面体勾勒大千世界[13]”，几何对人类而言是重要的内容，虽然教学中会遇到许多困难，但只要多实践多反思总结，相信聋生学习图形与几何的成绩一定会越来越好！

[1]周玮,赵斌.论聋生数学思维的培养策略[J].绥化学院学报,2014(4):64.

[2]张凤琴.聋人与听力正常人图形视认知的比较与大脑左右半球功能不对称性的关系[J].中国特殊教育，2000（1）：18.

[3]北师大，等.在职攻读教育硕士专业学位全国统一考试大纲及指南[M].北京：北京师范大学出版社，2011：275.

[4]厦门网.85后聋女考取美4所高校博士读唇考过六级听力[EB/OL]http://news.xmnn.cn/a/shxw/201306/t20130606_335 8889.htm，2013-06-06.

[5]关志成.初中几何教学研究[M].北京：教育科学出版社，2002:24，20，19.

[6]王建磐.义务教育课程标准试验教科书数学初中一年级（七年级）（上）[S].上海：华东师范大学出版社，2008：10.

[7]中华人民共和国教育部.义务教育数学课程标准(2011年版）[M].北京：北京师范大学出版社，2012:8，2.

[8]教育部基础教育课程教材专家工作委员会.义务教育数学课程标准（2011年版）解读[M].北京师范大学出版社，2012：271，85，85.

[9]钱佩玲.数学思想方法与中学数学[M].北京师范大学出版社，2008：93，92.

[10]喻平.著名特级教师教学思想录:中学数学卷[M].江苏：江苏教育出版社，2012.

[11]课程教材研究所.新中国中小学教材建设史1949—2000研究丛书:数学卷[M].北京：人民教育出版社，2010:317.

[12]鲍建生，周超.数学学习的心理基础与过程[M].上海：上海教育出版社，2012:4.

[13]邬桂红.加减乘除演绎无限苍穹点线面体勾勒大千世界[EB/OL].http://www.jxpanxi.net/Article/ShowArticle.aspArticleID=289，2015-12-24.

[责任编辑刘金荣]

G762

A

2095-0438（2016）04-0041-04

2015-01-25

吴光安(1982－)，男，福建龙岩人，厦门市特殊教育学校一级教师，研究方向：中学数学教育，特殊教育。

2014年福建省中小学教师发展基金课题“聋校高中数学校本教材研究”（FZJJ20130201954）。