一类具有治愈率和时滞的传染病动力学模型的稳定性
管宪伟,李梁晨
(军械工程学院应用数学研究所,河北石家庄 050003)
一类具有治愈率和时滞的传染病动力学模型的稳定性
管宪伟,李梁晨
(军械工程学院应用数学研究所,河北石家庄050003)
研究了一类具有时滞的传染病动力学模型的性质,在模型中考虑了治愈率以及饱和因素对疾病传播的影响.通过分析特征方程,讨论了模型各个平衡点的局部稳定性,得到了模型Hopf分支存在的充分条件.证明了当基本再生数大于1时,疾病是持续生存的.通过构造Lyapunov泛函,得到了无病平衡点全局稳定的充分条件.
治愈率;时滞;饱和发生率;持久性;全局稳定性;Hopf分支
【引用格式】管宪伟,李梁晨.一类具有治愈率和时滞的传染病动力学模型的稳定性[J].北华大学学报(自然科学版),2016,17 (3):290-295.
1 引 言
近些年来,随着各类传染病在世界范围内的爆发,人们的生活正在遭受传染病的威胁.为了更好地了解传染病的传播机制,控制传染病的传播,传染病感染动力学模型越来越受到人们的关注[1].文献[2]研究了一类带有注射治疗的随机SIS动力学模型,讨论了模型的灭绝和持续生存的条件:
其中:S(t),I(t),V(t)分别表示t时刻的易感者,感染者和由于注射治疗获得免疫的人群的数量;A代表一个常数的出生率;β表示S和I之间的感染速率;γ表示感染者的恢复速率;μ表示三类人群的自然死亡率;δ表示感染者因病造成死亡的速率;ε表示接受注射的人群失去免疫的速率.文献[2]分别讨论了系统(1)疾病持续生存和灭绝的条件.
本文在模型(1)的基础上,研究了一类具有时滞和治愈率的传染病动力学模型,并且考虑了饱和发生率的因素.这里我们将人群分为易感者S(t)和疾病感染者I(t),针对易感者考虑具有logistic增长率的模型:
其中:βS(t)I(t)表示疾病感染者成功接触并且感染易感者的速率;μ表示感染者的正常死亡率;δ表示感染者因感染疾病死亡的速率;γ表示感染者经过治愈后变回易感者的速率.
模型(2)满足的初始条件如下:
容易证明,当t>0时,模型(2)满足初始条件(3)的解是正的,故我们只需在2}上考虑模型(2).
2 局部稳定性和Hopf分支的存在性
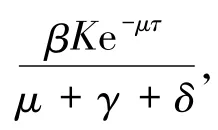
模型(2)在平衡点E0处的特征方程为
容易看出方程(4)的两个根分别为r,-(μ+γ+δ),方程(4)存在正的特征根,故平衡点E0是不稳定的.
同理,我们可以得到模型(2)在平衡点E1处的特征方程为
容易看出方程(5)的一个根为-r,其他根由方程
决定.假设方程(6)存在具有非负实部的特征根,将方程变形为
将该方程两边分别取模,得到
当R0<1时,方程的右端满足
矛盾.因此当R0<1时,特征方程(5)的所有根均具有负实部,此时E1是稳定的.
当R0>1时,f(0)<0,f(+∞)=+∞,故方程(5)存在正实部的特征根,此时E1是不稳定的.
当τ=0时,模型(2)在正平衡点E*处的特征方程为
其中
因为P>K>K e-μτ,当R0>1时
如果μ+γ+δ>r,那么q>0,此时方程(7)两个根均具有负实部,正平衡点E*是稳定的.
当τ≠0时,模型在E*处的特征方程为
其中
下面应用文献[3-4]中的方法来证明模型(2)Hopf分支的存在性.
整理得
其中C1=p21-2p2-q21,C2=p22-q22.记σ=ω2,
因此,如果方程(8)有纯虚根,那么
令
定理1假定特征方程形式如下
其中f0(s),f1(s)关于s连续可微.方程(12)的一个根为s(τ)=α(τ)+iω(τ),其中s(τ)关于τ连续可微,并且对于正数τ0满足α(τ0)=0,ω(τ0)=ω0.记
那么有
这样,令f0(s)=s2+p1s+p2,f1(s)=q1s+q2,根据式(9)和(13)的定义知φ(ω)=G(ω2),因此可得以下推论:
因此,根据文献[5]中的Hopf分支定理,得到如下结果:
定理2(ⅰ)对于所有的τ≥0,如果方程(10)没有正根,地方病平衡点E*局部渐近稳定.
(ⅱ)如果方程(11)有正根,那么平衡点E*在区间τ∈[0,τ0)内局部渐近稳定,其中,并且如式(11)定义.
(ⅲ)如果ωn0是方程(10)的根,那么当τ增加,在τ=τ0时,模型(2)出现Hop f分支.
3 持久性
本节引用Hale和Waltman[6]持久性定理来证明模型(2)的持久性.
引理1存在正常数M1,M2,使得对于模型(2)任意满足初始条件(3)的正解满足
注意到
两边从t-τ到t积分得
整理得到
因此
注意到
整理得
故
取d0=,因此有
证毕.
定理3如果R0>1,那么模型(2)是持久的.
选取充分小的ε,满足
让t0充分大,使得当t≥t0-τ时
所以,当t>t0时
又因为
那么
4 全局稳定性
定理4如果R0<1并且满足≥r,那么无病平衡点E1是全局渐近稳定的.
证明:令
对V(t)沿着模型(2)的正解求导得
由式(14)可得
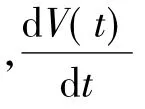
5 数值模拟
固定参数值r=0.1,K=100,β=4.8,α=1.2,μ=0.4,γ=δ=0.3,选取初值为(0.5,1.4),通过计算可以得到模型(2)的两个非平凡平衡点分别为E0(100,0)、地方病平衡点E*(S*,I*)=(0.320 8,0.026 8).
通过式(12)可以算出,当τ0=2.581 2时,模型(2)出现Hopf分支,见图1.当τ=0.5时,系统的地方病平衡点E*(0.320 8,0.026 8)是局部渐近稳定的,见图2.
[1]马知思,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京:科学出版社,2007.
[2]Yanan Zhao,Daqing Jiang,Donal O’Regan.The extinction and persistence of the stochastic SIS epidemic model with vaccination[J].Physica A,2013,392:4916-4927.
[3]Tianlei Wang,Zhixing Hu,Fucheng Liao.Stability and Hopf bifurcation for a virus infection model with delayed humoral immunity response[J].JMath Anal Appl,2014,411:63-74.
[4]魏俊杰,王洪滨.时滞微分方程的分支理论及应用[M].北京:科学出版社,2012.
[5]B D Hassard,N D Kazarinoff,Y H Wan.Theory and applications of Hopf bifurcation[M].Cambridge:Cambridge University Press,1981.
[6]JHale,PWaltman.Persistence in infinite-dimensional systems[J].SIAM JMath Anal,1989,20:388-395.
【责任编辑:伍林】
Stability and Hopf Bifurcation of a SIS Model with Time Delay and Cure Rate
Guan Xianwei,Li Liangchen
( Institute of Applied Mathematics,Mechanical Engineering College,Shijiazhuang 050003,China)
A SIS model with time delay and cure rate is studied.By analyzing the corresponding characteristic equations,the local stability of every feasible equilibria is investigated. It proved that the disease is permanent when the reproduction number is greater than 1. By constructing appropriate Lyapunov functional,a sufficient condition is obtained for the global stability of infection-free equilibrium.
cure rate; time delay; saturation incidence; permanence; global stability; Hopf bifurcation
O175.13
A
1009-4822(2016)03-0290-06
10.11713/j.issn.1009-4822.2016.03.002
2016-03-03
国家自然科学基金项目(11371368).
管宪伟(1990-),男,博士研究生,主要从事微分方程与动力系统研究,E-mail:schianway@163.com.

