分析采取措施对性病传播动态的影响
胡慧敏,乔志琴
(中北大学理学院,太原 030051)
近年来,性传播疾病的爆发引起了人们的广泛重视,卫生界医疗界等各界的学者们也都致力于减少或停止性病的传播.其中,使用数学模型来分析性传染病的传播和控制尤为重要.典型的传染病模型包括易感感染(SI)模型,易感感染易感(SIS)模型和易感感染恢复(SIR)模型[1].根据疾病扩散的不同特征来使用不同的模型,本文使用SIRS模型.与SIR模型不同,SIRS模型考虑短期免疫.所谓的短期免疫是指免疫个体在一段时间后成为易感个体.
众所周知,人之间的不断接触与联系为疾病的传播定义了一个网络.因为个体之间相互连接,相互交错,就需要通过了解个体之间的联系来了解和预测疾病的传播.在网络流行病中,把人看作网络上的节点,每个节点对应一个个体,个体之间的相互接触与联系表示他们之间的局部作用.但在经典的流行病模型中,每个人之间的接触被忽略,不太符合实际.本文考虑到不同的人在单位时间内接触的人数可能不同,增加了研究的真实性与可行性[2-14].
之前的一些模型中将染病者分为低风险染病者和高风险染病者,一旦被感染,一部分感染者开始控制他们的行为,比如采用避孕套来保护他们的伴侣[15].为了更好地预防艾滋病,本文研究未感染时采取措施对艾滋病的影响.在性生活中,一部分人使用避孕套,另一部分人不使用.所以,使用避孕套的这部分人在与有性病者进行性生活时感染的风险比较小,称他为低风险易感者,同理,不使用避孕套者称之为高风险易感者,当他们受到感染时都将变成染病者.
本文讨论了一种在复杂网络中的SIRS流行病模型.第一节中,给出了模型的基本公式.第二节中,讨论了只有低风险易感者时的模型,运用下一代矩阵法得出了基本再生数并讨论了无病平衡点的稳定性,还讨论了地方性平衡点的存在性并通过构造合适的李雅普诺夫函数,研究了地方性平衡点的全局稳定性.第三节中,讨论了只有高风险易感者时,性病相应的传播动态.在第四节中,讨论了高风险易感者和低风险易感者并存时,性病相应的传播动态.在第五节中,通过数值模拟来说明采取措施可以减少性病的传播.在最后一节,进行了简短的讨论.
1 模型的建立
本节在复杂网络上构建流行病模型.所谓网络是由大量节点与连接两个节点之间的一些边构成,其中节点代表真实系统中不同的个体,而边则表示个体间的关系.为了反映个体生理能力和生存空间的局限性,将总节点(即网络大小)假设为常数N.模型中,每个节点对应一个个体,个体之间的相互接触看成有边相连.
首先,对节点进行分类,即对个体进行分组,一个个体在单位时间内接触的人数k就是网络中节点的度,每个个体的度分布是稳定的,节点之间是相互独立且状态不同的[16].根据单位时间内接触人数的不同将节点按度分为k类,其中k=(1,2,…,n).用常数Nk来表示单位时间内接触人数为k的人群的相对密度.
其次,对节点的状态进行分类,节点可以分为4种状态:低风险易感者s1k,高风险易感者s2k(通过避孕套的使用率p划分低风险易感者和高风险易感者),感染者ik和恢复者rk.其中,s1k表示度为k时低风险易感者的相对密度.同理,s2k,ik,rk分别表示度为k时高风险易感者,染病者,恢复者的相对密度.其中,s1k+s2k+ik+rk=Nk.显然,s1k+s2k=Nk-(ik+rk),当避孕套使用率为p时,低风险易感者的相对密度为s1k=p[Nk-(ik+rk)],同理,s2k=(1-p)[Nk-(ik+rk)].其中,0≤p≤1.
在模型中,低风险易感者和高风险易感者通过接触感染者变为染病者,低风险易感者与染病者的接触率为Θ11(t),高风险易感者与染病者的接触率为Θ22(t).β1为低风险易感者与染病者接触时的有效传染率,β2为高风险易感者与染病者接触时的有效传染率,所以,低风险易感者与染病者的有效接触率为Θ1(t)=β1Θ11(t),高风险易感者与染病者的有效接触率为Θ2(t)=β2Θ22(t).染病者通过一定的恢复率γ变为恢复者,恢复者失去免疫力后又变为相应的易感者,其中,变为低风险易感者时失去免疫力率为δ1,变为高风险易感者时失去免疫力率为δ2.根据生物学意义β1>0,β2>0,γ>0,δ1>0,δ2>0.其中,
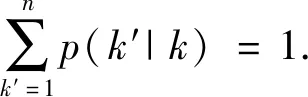
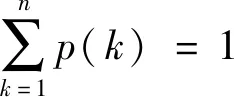
基于以上阐述,构建的传输图如图1所示.
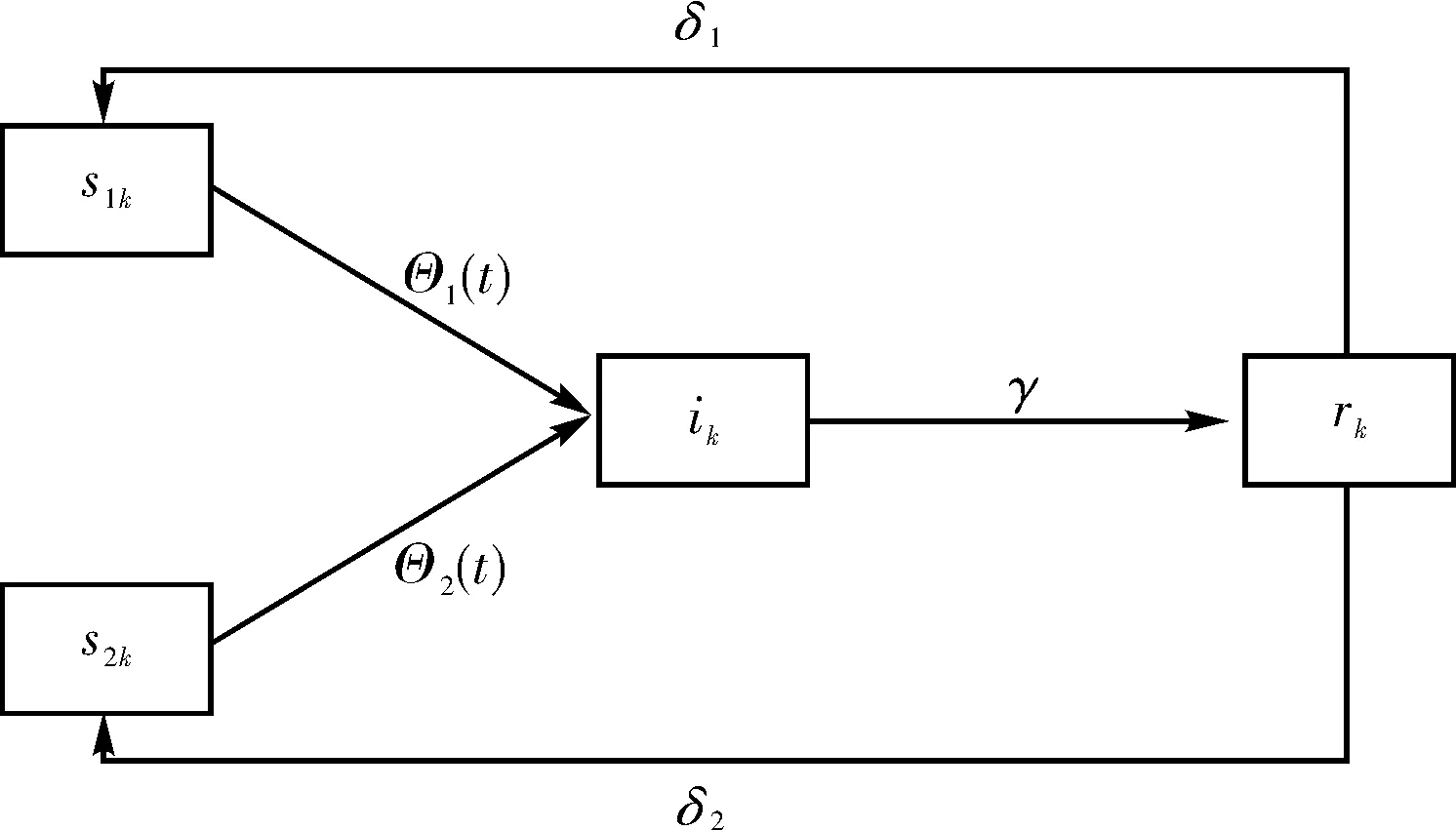
图1 传输图Fig.1 Transmission chart
由图1的传输图可以很容易得到下面的系统(1).
(1)
2 只有低风险易感者(p=1)
当p=1时,避孕套的使用率为1,即系统中的所有人都使用避孕套.此时,只有低风险易感者,即当p=1时,s2k=(1-p)[Nk-(ik+rk)]=0,因为此时高风险易感者为0,所以当恢复者失去免疫力后也不可能再变为高风险易感者,所以δ2=0.
系统(1)变为
(2)
2.1 基本再生数和无病平衡点的全局渐近稳定性
基本再生数决定了流行病模型的全球动态,在这里用下一代矩阵法来计算它.
将s1k=p[Nk-(ik+rk)]=Nk-ik-rk代入系统(2)得到
(3)
令ik=0,rk=0,可以得到系统(3)的无病平衡点为
由系统(3)得到:
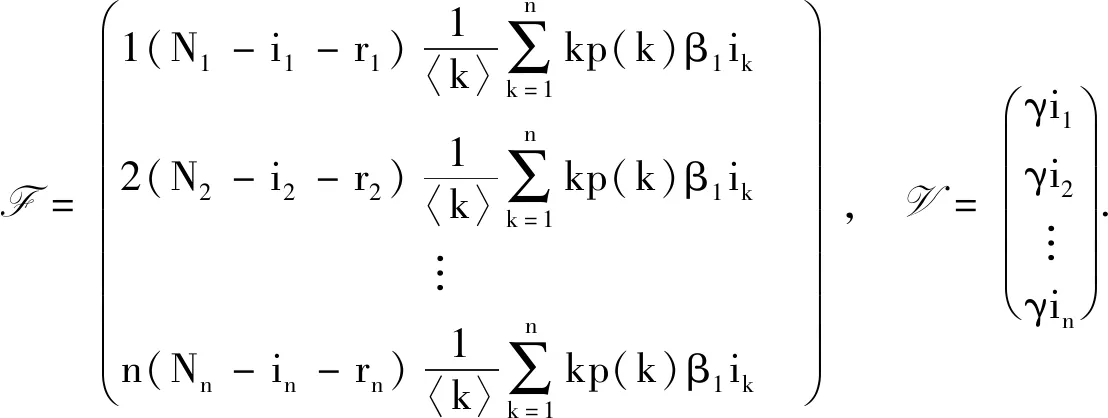
在F中第一行分别对i1,i2,…,in求导得到F的第一行,第二行分别对i1,i2,…,in求导得到F的第二行,以此类推得到下面的F.
用a1=1(N1-i1-r1),a2=2(N2-i2-r2),…,an=n(Nn-in-rn)得
F=
在V中第一行分别对i1,i2,…,in求导得到V的第一行,第二行分别对i1,i2,…,in求导得到V的第二行,以此类推得到下面的V:

求FV-1得

则
R01=
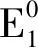

L1=WV-1x,
对其进行求导,
(R01-1)Wx≤0.
显然,当R01<1时系统(3)的无病平衡点全局渐近稳定.
2.2 地方性平衡点的存在性与稳定性
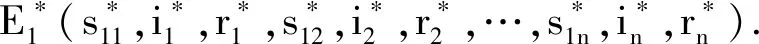
其中
结合
解得
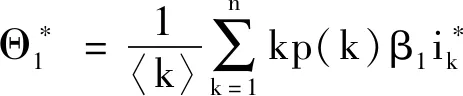
定义一个方程

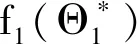
所以

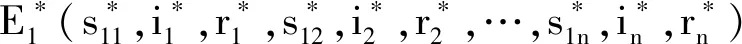
证明构建下面的李雅普诺夫函数:
因
再结合等式
和

对V1(t)求一阶导可得:

得
由Lasalle不变集原理,有
3 只有高风险易感者(p=0)
当p=0时,避孕套的使用率为0,即系统中无人使用避孕套,此时,只有高风险易感者,即当p=0时,s1k=p[Nk-(ik+rk)]=0,因为此时低风险易感者为0,所以当恢复者失去免疫力后也不可能再变为低风险易感者,所以δ1=0.
系统(1)变为
(4)
再结合s2k=(1-p)[Nk-(ik+rk)]=Nk-ik-rk,系统(4)变为
(5)
类似于p=1,当p=0时,计算其基本再生数得:
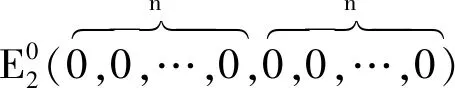
4 高风险易感者和低风险易感者并存(04.1 基本再生数和无病平衡点的稳定性
当高风险易感者和低风险易感者并存即0(6)
令ik=0,rk=0,此时系统人口中使用避孕套率为p,不使用避孕套率为1-p,由s1k(t)=p[Nk-(ik+rk)],s2k(t)=(1-p)[Nk-(ik+rk)].其中,0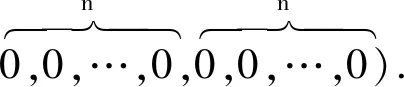
类似于p=1,用下一代矩阵法计算R0.
在F中第一行分别对i1,i2,…,in求导得到F的第一行,第二行分别对i1,i2,…,in求导得到F的第二行,以此类推得到下面的F:

在V中第一行分别对i1,i2,…,in求导得到V的第一行,第二行分别对i1,i2,…,in求导得到V的第二行,以此类推得到下面的V:

求FV-1得
则基本再生数为
则系统(6)的基本再生数为
定理3如果R0<1则系统(6)的无病平衡点E0是全局渐近稳定的,疾病将消失.

因ρ(FV-1)=ρ(V-1F)=R0且V-1F非负不可约,则存在一个正的左特征向量A对应于特征值ρ(V-1F) ,AV-1F=R0A.考虑下面的李雅普诺夫函数:
L=AV-1x>0.
对其进行求导得
AV-1(F-V)x=(R0-1)Ax≤0.
于是得R0<1时系统(6)的无病平衡点全局渐近稳定.
4.2 地方性平衡点的存在性
定理4当R0>1时系统(6)的地方性平衡点存在且唯一.
证明将s1k=Nk-s2k-ik-rk代入(6)得
(7)
其中
解得

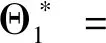
定义一个方程

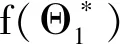


其中,



证得R0>1时系统(6)的地方性平衡点存在且唯一.
5 数值模拟
本节利用Matlab进行数值模拟,观察随着避孕套使用率的不同和度k的不同染病者的相对密度的变化.
首先,取定参数δ1=0.2,δ2=0.3,γ=0.05,β1=0.2,β2=0.5.k分别取10,30,50,100.
图2中,观察可知当p相同时随着k的增大ik在增大,即当避孕套使用率相同时随着接触人数的增加,染病者的相对密度在增加,说明接触的人越多疾病传播的范围越广.当k相同时随着p的增大ik在减小,即当接触的人数相同时随着避孕套使用率的增加,即采取措施的人数在增加,染病者的相对密度在减少.由此可见,采取措施可以减少疾病的传播.

图2 变化图Fig.2 Change chart
6 结论
本文主要研究采取措施对性病传播的影响.通过避孕套的使用率划分了低风险易感者和高风险易感者,在异质网络上构建模型并给出基本再生数,然后研究无病平衡点及地方性平衡点的稳定性.最后,通过数值模拟可以直观看出避孕套的使用率影响性病的传播.所以,为了保护自己,减少性病的传播,在性生活中采取措施是必不可少的.
猜你喜欢
考虑媒体影响的一类时滞传染病模型的分岔周期解延边大学学报(自然科学版)(2023年4期)2024-01-05 09:23:24 一类具有年龄结构和接种干预的手足口病模型动力学分析北华大学学报(自然科学版)(2023年3期)2023-05-22 09:11:16 偶感青年文学家(2022年13期)2022-07-06 02:16:00 扒一扒“戴套”的尴尬事大众健康(2021年9期)2021-10-28 11:52:34 均匀网络上SIR模型三种不同逼近方法比较安阳师范学院学报(2018年5期)2018-11-21 06:43:48 爱 情诗选刊(2016年9期)2016-11-26 13:47:43 一类受媒体影响的随机HIV模型信阳师范学院学报(自然科学版)(2016年2期)2016-08-09 03:39:12 食饵染病生态流行病系统的稳定性与最优收获集美大学学报(自然科学版)(2015年1期)2015-02-28 01:13:33 我国HIV/TB双重感染者血清细胞因子水平的研究中国医科大学学报(2014年3期)2014-05-25 01:44:22 在巴基斯坦城市,广告活动对避孕套使用的影响中国计划生育学杂志(2012年2期)2012-01-26 21:36:27
4.1 基本再生数和无病平衡点的稳定性
当高风险易感者和低风险易感者并存即0 (6) 令ik=0,rk=0,此时系统人口中使用避孕套率为p,不使用避孕套率为1-p,由s1k(t)=p[Nk-(ik+rk)],s2k(t)=(1-p)[Nk-(ik+rk)].其中,0 类似于p=1,用下一代矩阵法计算R0. 在F中第一行分别对i1,i2,…,in求导得到F的第一行,第二行分别对i1,i2,…,in求导得到F的第二行,以此类推得到下面的F: 在V中第一行分别对i1,i2,…,in求导得到V的第一行,第二行分别对i1,i2,…,in求导得到V的第二行,以此类推得到下面的V: 求FV-1得 则基本再生数为 则系统(6)的基本再生数为 定理3如果R0<1则系统(6)的无病平衡点E0是全局渐近稳定的,疾病将消失. 因ρ(FV-1)=ρ(V-1F)=R0且V-1F非负不可约,则存在一个正的左特征向量A对应于特征值ρ(V-1F) ,AV-1F=R0A.考虑下面的李雅普诺夫函数: L=AV-1x>0. 对其进行求导得 AV-1(F-V)x=(R0-1)Ax≤0. 于是得R0<1时系统(6)的无病平衡点全局渐近稳定. 定理4当R0>1时系统(6)的地方性平衡点存在且唯一. 证明将s1k=Nk-s2k-ik-rk代入(6)得 (7) 其中 解得 定义一个方程 其中, 证得R0>1时系统(6)的地方性平衡点存在且唯一. 本节利用Matlab进行数值模拟,观察随着避孕套使用率的不同和度k的不同染病者的相对密度的变化. 首先,取定参数δ1=0.2,δ2=0.3,γ=0.05,β1=0.2,β2=0.5.k分别取10,30,50,100. 图2中,观察可知当p相同时随着k的增大ik在增大,即当避孕套使用率相同时随着接触人数的增加,染病者的相对密度在增加,说明接触的人越多疾病传播的范围越广.当k相同时随着p的增大ik在减小,即当接触的人数相同时随着避孕套使用率的增加,即采取措施的人数在增加,染病者的相对密度在减少.由此可见,采取措施可以减少疾病的传播. 图2 变化图Fig.2 Change chart 本文主要研究采取措施对性病传播的影响.通过避孕套的使用率划分了低风险易感者和高风险易感者,在异质网络上构建模型并给出基本再生数,然后研究无病平衡点及地方性平衡点的稳定性.最后,通过数值模拟可以直观看出避孕套的使用率影响性病的传播.所以,为了保护自己,减少性病的传播,在性生活中采取措施是必不可少的.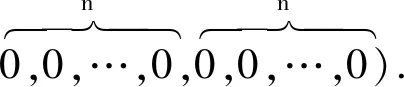



4.2 地方性平衡点的存在性

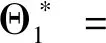

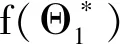





5 数值模拟

6 结论

