均匀网络上SIR模型三种不同逼近方法比较

王治萍

(朔州师范高等专科学校 数学与计算机系，山西 朔州 036000)

0 引言

考虑静态均匀网络上的SIR对逼近传染病模型,即网络的规模N保持不变,网络的结构保持不变。其中节点的状态有三种状态,易感状态S和染病状态I以及恢复状态R; 并且[S]表示网络中处于易感状态的节点(即易感者)数量，[I]表示网络中处于染病状态节点(即染病者)的数量，[R]表示网络中处于恢复状态节点(即恢复者)的数量。[SI],[SS],[SR],[II],[IR]表示网络中二元组(对)状态为S-I,S-S,S-R,I-I,I-R的数量。[SSI],[ISI],[RSI]表示网络中状态为S-S-I,I-S-I,R-S-I三元组的数量。一个染病者和一个易感者的接触传染率为λ，染病者的恢复概率为γ0。应用主方程可得关于[S],[I],[SI],[SS],[SR],[II],[IR]的微分方程组如下

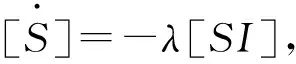
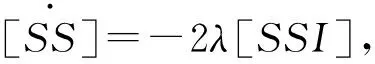
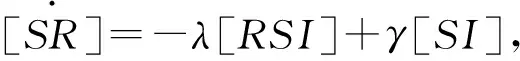
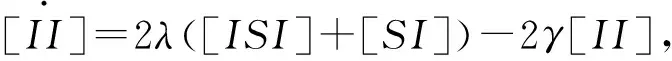
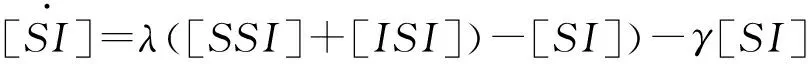
(1)

[S]+[I]+[R]=N,

[SS]+2[SR]+2[IR]+[II]+2[SI]=n1N

(2)

1 三种研究方法对比

下面应用三种不同的逼近方法封闭模型进而研究这三种逼近方法的优劣。

1.1 Poission分布下的SIS对逼近模型(P-PW)

当节点的染病状态I邻居数服从泊松(Poission)分布时，存在以下的三元组逼近公式

结合(2)式可以对系统(1)进行封闭和降维，然后得到染病邻居数服从Poission分布时SIR对逼近传染病模型(P-PW)如下

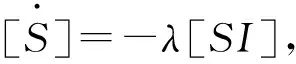
(3)

下面可得无病平衡点为P1(N,0,n1N,0,0,0)，其中染病仓室为[I],[SI]运用下一代再生矩阵的方法可得

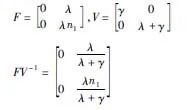
1.2 多项式分布下的SIR对逼近模型(B-PW)

当节点的染病状态I邻居数服从多项式分布时，存在以下的三元组逼近公式

同样结合(2)式对系统(1)进行封闭和降维，然后得到染病邻居数服从多项式分布是SIS对逼近传染病模型(B-PW)。

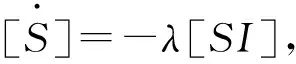
(4)

可得无病平衡点为P1(N,0,n1N,0,0,0)，其中染病仓室为[I],[SI]运用下一代再生矩阵的方法可得

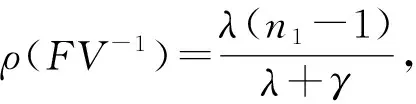
1.3 平均场SIR对逼近模型(MF-PW)

Kiss基于平均场思想提出了三元组的另一种逼近公式

同样结合(2)式可以对系统(1)进行封闭和降维，然后得到相应SIR对逼近传染病模型(MF-PW)。

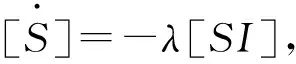
可得无病平衡点为P2(N,0,n1N,0,0,0),其中染病仓室为[I],[SI]运用下一代再生矩阵的方法可得

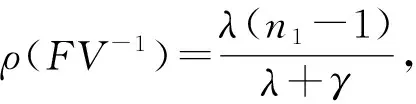
2 结论

由以上讨论可知，节点的染病邻居数服从泊松分布所得疾病的基本再生数大于染病邻居数，服从多项式分布和基于平均场逼近方法得到的基本再生数；同时染病邻居数服从多项分布和基于平均场逼近方法得到的基本再生数相同。