Matlab图像滤波处理技术研究

关雪梅

(辽宁对外经贸学院 基础课教研部，辽宁 大连 116052)

数字图像在传输过程中会受到成像设备和环境的干扰而产生噪声图像，我们可以采用滤波的方法来减少图像中的噪声，该方法是数字图像处理技术中非常重要的一部分内容。由于噪声在频谱图像中具有丰富的高频分量，因而我们采用低通滤波的方法，保留低频部分的信息，去除高频部分的信息，从而实现平滑去噪的滤波效果。

Matlab是由美国MathWorks公司于1984年推向市场，经过了30多年的发展，如今已成为社会认同的非常优秀的技术应用软件。Matlab主要用来进行可视化图形图像处理和数值计算分析的工具语言，名字是由Matrix( 矩阵) 和Laboratory(实验室)的两个单词的前三个字母组合在一起而形成的。Matlab将数字信号处理、仿真、矩阵计算、数值分析及数字图形图像处理等很多强大功能汇集在交互式计算机环境中来使用，为一些领域的科学研究和应用提供了一个有效的平台。Matlab平台还提供各种功能的工具箱，可以用来处理某些领域的特定问题，这些工具箱算法的使用是可扩充的，开放的，用户不仅可以使用工具箱已有的算法，还可以在这个基础上进行修改或开发来为某些特定的功能服务。本文主要在Matlab中实现四种低通滤波器的设计，通过比较分析，在对数字图像进行处理时，针对不同的情况选取不同的滤波方法，从而达到图像滤波效果的最优化。

1 图像低通滤波原理及算法

在对数字信号频率的特性进行分析时，图像高频分量一般分布在图像边缘、跳跃部分以及颗粒噪声区域，而低频分量则是大面积的背景区域。因而我们采用低通滤波的方法就可以除去图像中的高频分量，使图像中的噪声得到削减，实现平滑效果。

图像低通滤波原理如下：

G(u,v)=F(u,v)(H(u,v))

其中F(u,v)是含有噪声的原始图像的傅里叶变换，G(u,v)是经过平滑图像处理后的傅里叶变换，H(u,v)是传递函数。合理的选取H(u,v)，利用传递函数使得F(u,v)图像中的高频信号得到削弱，实现G(u,v)图像后再对图像进行反傅里叶变换就可以达到最终我们想要的效果g(x,y)。我们可以看出H(u,v)含有低通滤波的特点，实现图像平滑处理效果，我们把它称作图像低通滤波法。在Matlab中实现低通滤波主要代码功能如下：

i=imread(’lena.tif’) %读入lena图像

j=fft2(double(i)) %进行图像傅里叶变换

j=fftshift(j) %频谱平移

k=j.*hd %图像滤波

k=ifftshift(k)

iout=ifft2(k) %进行反傅里叶变换

2 Matlab处理图像中低通滤波器设计

采用Matlab工具箱进行频域滤波处理图像时，没有特定的函数，因而我们在利用Matlab来对图像进行平滑滤波处理时需要自己来构造。常用的频域低通滤波器有理想低通滤波器(Ideal Low Pass Filter 缩写为ILPF)、指数低通滤波器(Exponential Low Pass Filter 缩写为ELPF)、巴特沃斯低通滤波器(Butterworth Low Pass Filter 缩写为 BLPF)和梯形低通滤波器(TLPF)。

2.1 图像理想低通滤波(ILPF)

假设在傅里叶平面上，理想的低通滤波器的截止频率到原点的距离为D0，则理想低通滤波器的传递函数为：

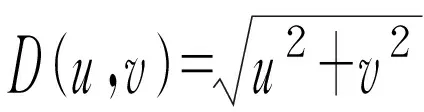
在Matlab中实现理想的低通滤波主要代码功能如下：

[m1,m2]=freqspace(size(i),’meshgrid’) %生成频率序

d=ones(size(i)) %构造滤波器大小

r=sqrt(m1.^2+m2.^2) %构造滤波器决策函数

d(r>0.1)=0 %构造滤波器，半径r>0.1

2.2 图像巴特沃斯低通滤波(BLPF)

Butterworth低通滤波器是图像处理中的一种电子滤波器，是当今图像处理领域中比较流行的一类数字滤波器，应用非常广泛。它是采用Butterworth函数作为滤波器的功能函数，具有最平坦的图像处理特性。ILPF可以在计算机模拟环境中实现，而且在数学领域中定义非常清晰，但不能用它来处理实际的电子设备。n阶Butterworth低通滤波器的传递函数(原点语截止频率的距离)为：

其中，D(u,v)=(u-M/2)2+(v-N/2)2

与理想的低通滤波器不同的是，Butterworth低通滤波器函数在被滤除的频率与通带之间截断不是很明显，它对图像的处理结果要好于理想的低通滤波器，但在阶数增高时振铃效应会成为一个主要的因素。以下我们采用二阶的Butterworth低通滤波器来进行图像处理，代码的核心部分如下：

y=imageread('lena.bmp')

imageshow(y)

s=imagenoise(y,'salt & pepper') %加入含有噪声的图像

figure,imageshow(s)

f=double(s) %数据类型转换

k=fseries2(f) %执行傅立叶变换

k=fseriesshift(k) %图像转换

[X,Y]=size(k)

n=2 %滤波器阶数

dd=50

x=ffix(X/2)

y=ffix(Y/2)

for i=1:X

for j=1:Y

d=sqrt((i-x)^2+(j-y)^2)

h=1/(1+0.414*(d/dd)^(2*n)) %图像的低通滤波器传递函数

ss(i,j)=h*g(i,j)

end

end

ss=ifseriesshift(ss)

figure,imageshow(ss) %处理后的图像

2.3 图像指数低通滤波(ELPF)

ELPF是对图像进行平滑处理的一种常用滤波器，传递函数为：

上式中的n代表衰减率的系数，当D(u,v)为D0时，则结果为

用指数低通滤波器进行图像噪声抑制时，图像的边缘细节处理结果比Butterworth滤波器处理模糊程度大，但图像中没有明显的振铃现象。代码的核心部分如下：

lena1=imread(‘lena.jpg’)

lena1=rgb2gray(lena1)

lena2=im2double(lena1)

lena3=imnoise(lena2,’gaussian’,0.02)

lena4=imnoise(lena3,’salt & pepper’,0.02)

f=fftshift(fft2(lena4))

[M,N]=size(f) %M和N分别代表行数和列数

s1=floor(M/2) %取整

s2=floor(N/2)

d0=35

for i=1:N

for j=1:M

d=sqrt((i-s1)^2+(j-s2)^2) %点(i,j)中心变换点的距离

h=exp(log(1/sqrt(2))*(d/d0)^2)

f(i,j)=h*f(i,j)

end

end

f=ifftshift(f)

f=im2uint8(real(ifft2(f)))

subplot(1,3,3),imshow(s),title(‘结果图像’)

2.4 图像梯形低通滤波(TLPF)

梯形低通滤波器处理图像的效果是理想的低通滤波器和具有平滑过渡带的低通滤波器的一个折中，有振铃效应，它的传递函数如下：

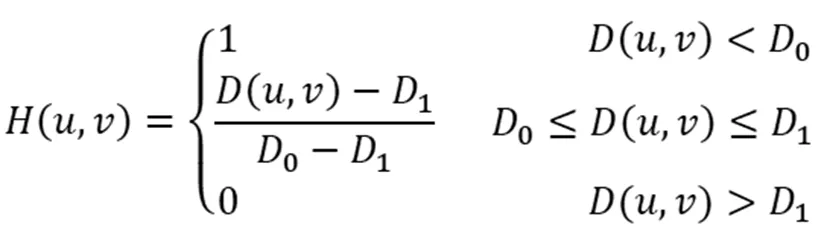
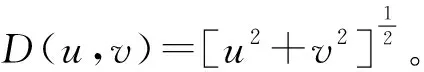
[m1,m2]=freqspace(size(i),’meshgrid’)

f=ones(size(i))

r=sqrt(m1.^2+m2.^2)

k1=0.1

k2=0.3

for i=1:size(i,1)

for j=1:size(i,2)

f(i,j)=(r(i,j)-k2)/(k1-k2)

end

end

f(rk2)=0 %设计滤波器

2.5 几种图像滤波处理实现

以下是通过Matlab进行几种图像滤波处理的实验结果：

本文主要进行图像滤波处理技术研究，实验结果可以看出，采用Matlab进行图像滤波处理方便简单，效率高，在数字图像处理领域具有很高的参考价值。

3 分析与总结

通过实验结果分析，在对图像进行滤波处理时，噪声平滑效果最好的是ILPF，但采用ILPF处理后的图像模糊，振铃程度加大。TLPF处理图像时，噪声平滑效果还可以，图像模糊和振铃程度都较轻，而ELPF和BLPF处理图像，噪声的平滑效果一般，但图像模糊程度较轻，无振铃现象。采用低通滤波器进行图像平滑处理可以削弱噪声，抑制伪轮廓的产生，但在对数字图像进行滤除噪声等干扰成分的同时，把图像中的一些有应用价值的高频率部分也会过滤掉，可以看出图像在对噪声等干扰进行低通滤波处理时会以牺牲图像细节为代价的，所以针对不同的情况选择合理的滤波方法非常重要。