IIR数字滤波器设计中频率转换探究

李艳凤，陈后金

（北京交通大学电子信息工程学院，北京100044）

0 引言

IIR数字滤波器设计是“数字信号处理”课程教学中的重要部分，也是教学的难点之一。IIR数字滤波器设计的一般过程如图1所示。

设计高通、带通和带阻滤波器可通过频率转换的方法实现，首先通过频率转换将模拟非低通滤波器技术指标转换为模拟低通滤波器的技术指标，该模拟低通滤波器称之为原型低通滤波器，然后通过复频率转换将原型低通滤波器的系统函数转换为对应的模拟滤波器系统函数。

在转换为原型低通滤波器的技术指标时，需要对参数进行选择。但现有模拟域频率转换的教学大多只给出参数选择结论，并没有对整个转换过程进行分析，这使得学生难以理解转换的原理以及参数选取的准则。为了解决这一问题，本文对整个模拟域频率转换过程进行分析，通过图形对转换过程中参数如何选取进行阐明，便于教师教学和学生理解。

图1 IIR数字滤波器设计的一般过程

1 模拟域频率转换

1．1 高通滤波器转换为原型低通滤波器

图2（a）为待设计高通滤波器的幅频响应，根据式（2）频率映射关系可得原型低通滤波器的幅频响应，如图2（b）中实线所示。由于物理可实现滤波器的系统函数为实系数，其幅频响应具有偶对称特性。依据原型低通滤波器幅频响应需具有的对称特性，构建其正频率部分对称的幅频响应，如图2（b）中虚线所示。根据图2（b）中虚线部分可得，此原型低通滤波器的设计指标：通带截止频率和阻带截止频率，即

图2 由高通滤波器转换为原型低通滤波器

1．2 带通滤波器转换为原型低通滤波器

根据式（5）确定的频率映射关系，可将带通滤波器的设计指标（ωs1，ωp1，ωp2，ωs2）映射到原型低通滤波器的设计指标其中，带通滤波器的中心频率ω0映射到原型低通滤波器的原点，带通滤波器的通带截止频率ωp1和ωp2分别映射到通常情况下（除非ω0

2＝ωs2ωs1），如图3（b）所示。也就是说，映射后的原型低通滤波器的幅频响应不具有偶对称，这样的低通滤波器无法直接设计。因此，我们需要根据映射后的原型低通滤波器构建一个幅频响应偶对称的原型低通滤波器。

图3 由带通滤波器转换为原型低通滤波器

图3（a）为待设计的带通滤波器的幅频响应，设ωs1＝160 π，ωp1＝200π，ωp2＝280 π，ωs2＝400 π。按照式（5）频率映射得到的原型低通滤波器（细线对应细线，粗线对应粗线），其幅频响应一般并不对称，需要选择或来构建幅频响应对称的原型低通滤波器。

1．3 带阻滤波器转换为原型低通滤波器

将，s＝jω 代入式（9），得到原型低通滤波器与带阻滤波器的频率映射关系为

根据式（10）确定的频率映射关系，其将带阻滤波器的设计指标 （ωp1，ωs1，ωs2，ωp2）映射为原型低通滤波器的设计指标其中，带阻滤波器的中心频率ω0映射到∞，带阻滤波器的阻带截止频率ωs1和 ωs2分别映射到通常情况下，需要选择其中一个作为原型低通滤波器的通带截止频率。与带通滤波器类似，现有教材直接给出选择绝对值较大的一个作为通带截止频率＝max［3～4］。下面对选择原因进行分析，由带阻滤波器设计指标（ωp1，ωs1，ωs2，ωp2）设计原型低通滤波器的过程如图4所示。

图4（a）为待设计的带阻滤波器的幅度响应，设ωp1＝160 π，ωs1＝ 200 π，ωs2＝280 π，ωp2＝500 π。按照式（10）频率映射得到的原型低通滤波器（左右对应位置出现反转），其幅频响应一般并不对称，需要选择）或来构建一个偶对称幅频响应的原型低通滤波器。

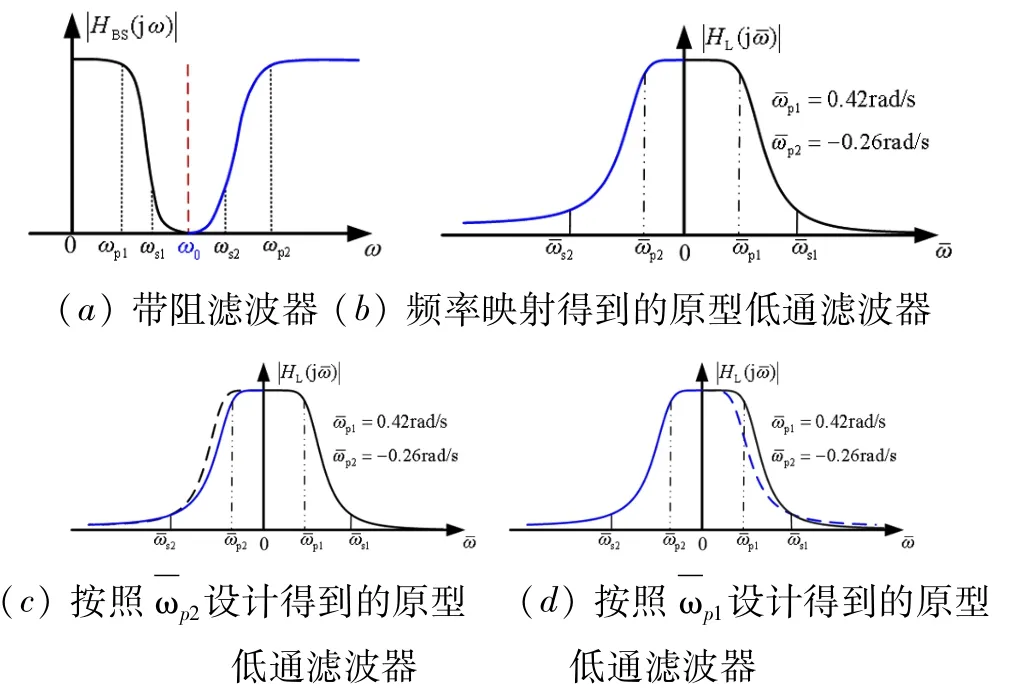
图4 由带阻滤波器转换为原型低通滤波器

根据此设计指标，在ωp2到0之间的通带频率范围内，构建的原型低通滤波器的幅频响应比要求的幅频响应高，最后设计出的带阻滤波器将会满足原带阻滤波器的设计指标。

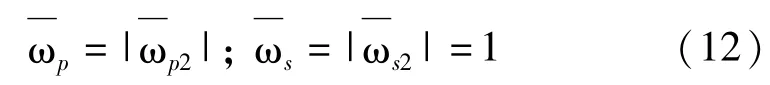
根据此设计指标，在0到ωp1之间的通带频率范围内，构建的原型低通滤波器的幅度响应比要求的幅度响应低，最后设计出的带通滤波器将无法满足原带通滤波器的设计指标。因此，对于带阻滤波器，应选取绝对值较大的｜作为原型低通滤波器的阻带截止频率，即

2 结语

针对现有IIR数字滤波器设计中模拟域频率转换教学方法存在的问题，本文分析了其他类型滤波器转换为原型低通滤波器的幅频响应的对应关系。当带通和带阻滤波器通过模拟域频率转换映射到原型低通滤波器时，该原型低通滤波器的幅频响应一般不满足偶对称，通过构建偶对称的幅频响应的过程，清晰地诠释了滤波器设计过程中参数选取的原理，有助于教师教学和学生理解。