一种改进的求解单调变分不等式的平行分裂算法

陈小彪,张玫玉,高玉洁,寇 静

(太原工业学院 理学系, 山西 太原 030008)

1 引言

自从二十世纪六十年代以来,有限维变分不等式的理论和算法得到了迅速的发展,并且广泛地应用到经济平衡理论,交通运输,社会经济模型,凸优化等方面.因此,变分不等式问题的研究和应用已经成为了数学中的一个热点问题. 一个变分不等式问题就是找到一个向量u*∈Ω使得

(u-u*)TF(u*)≥0,∀u∈Ω

(1)

其中Ω是Rn中的一个非空闭凸集，F是从Rn到它自身的一个映射，在本文中我们考虑如下结构的变分不等式问题：

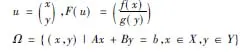
(2)

其中X⊂Rn1,Y⊂Rn2,A∈Rm×n1,B∈Rm×n2是给定的矩阵，b∈Rm是给定的向量，f:Rn1→Rn1,g:Rn2→Rn2是单调算子，对线性约束Ax+Bx=b引入拉格朗日乘子λ∈Rm,则(1)-(2)可表示为如下的紧凑形式(参考文献[1,2]):

找到一个向量w*=(x*,y*,λ)∈W使得

(w-w*)TF(W*)≥0,∀w∈W

(3)

(4)

我们用W*表示(3)-(4)的解.

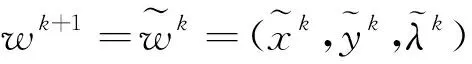
(5)

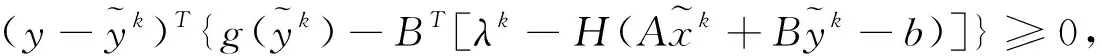
(6)

(7)

其中H∈Rm×m是一个给定的对称正定矩阵,可看做是对约束条件的罚参数,因此(1)-(2)的解是由求解一系列的(5)-(6)这样的低锥子单调问题得到的,而在许多实际问题中,它的求解释相当困难的.经典的交替方向法在文献中都已经有深入的研究,可看参考文献[1,2,5,6].

近来，一些渐进交替方向法PADM也得到了广泛的研究[7,8,9],特别的,在文献[7]中的PADM通过如下方法得到新的迭代点：

(8)

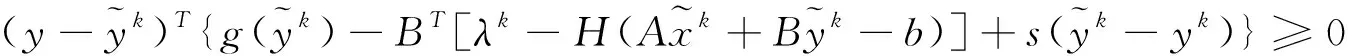
(9)

(10)

其中r,s大于0,可看做是渐进参数,则(8)-(9)是强单调变分不等式.文献[8]对这种渐进交替方向法做了改进,找到了一个下降方向和相应的最优步长.

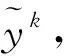
(11)

(12)

(13)

在每一次的迭代中(11)和(12)可以同时进行,这也是称它为平行分裂算法的原因.而(11)和(12)也只是单调的变分不等式,在实际情况中求解释相当困难的,受到文献[7]的启发,我们在子问题(11)和(12)中加入渐近项,则它们变为强单调的变分不等式,使得求解相对容易,并找到一个下降方向和沿着这个下降方向的最优步长,通过修正步来得到新的迭代点.

在整篇文章中,我们做出如下的假设:

(1)f(x)和g(y)是单调的,即

(x-x′)T(f(x)-f(x′))≥0,∀x,x′∈K

(y-y′)T(f(y)-f(y′))≥0,∀y,y′∈Y

(2)文中提到的变分不等式都是可解的,且解集非空.

2 改进的平行分裂算法

为了后面证明的方便,我们记

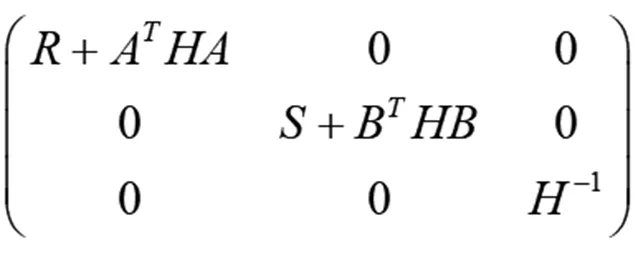
(14)

对给定的点wk=(xk,yk,λk)∈W,本文通过如下方法得到新的迭代点：

(15)

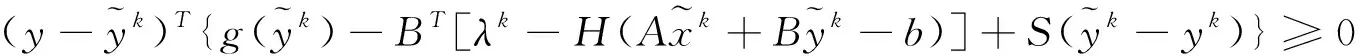
(16)

(17)

新算法

Step 0 ∀ε>0, 初始点w0=(x0,y0,λ0)∈Rn1×Rn2×Rm,G是(14)中所定义的矩阵，k=0

(18)

(19)

(20)

3 收敛性证明

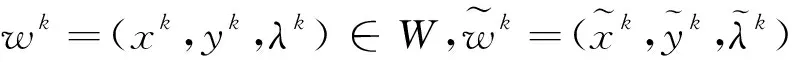
(21)

证明:利用柯西施瓦兹不等式得

(22)

(23)

(24)

则由(22),(23),(24)得

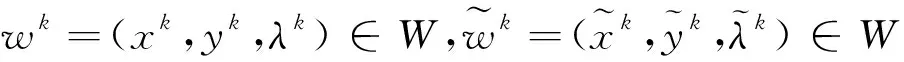
(25)

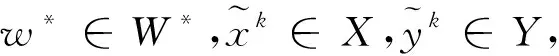
(26)

(27)

由(15),(16),(17)可得

(28)

(29)

(26)和(28)相加并利用f的单调性得

(30)

(27)和(29)相加并利用g的单调性得

(31)

(30)和(31)相加并利用Ax*+By*=b易得(25).证毕.

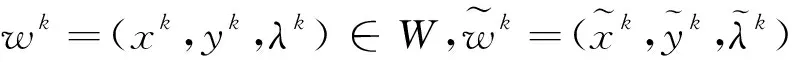
(32)

把(25)和(32)相加可得

(33)

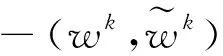
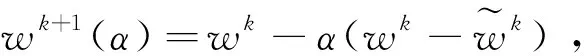
(34)

定理3.1w*=(x*,y*,λ*)∈W*,wk=(xk,yk,λk)是由新算法产生的序列点,则它满足

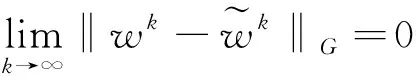
证明: 由(34)知道

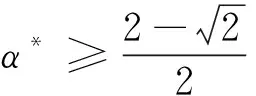
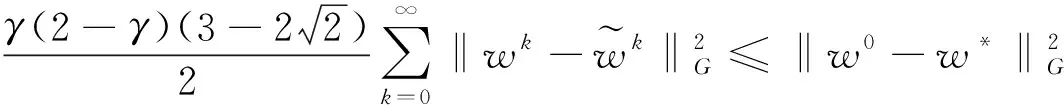
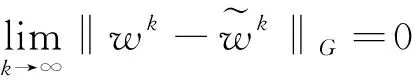
4 数值试验

我们考虑矩阵的逼近问题,其数学模型如下

C，HL和HU是给定的n×n对称矩阵.

则它可以转化为如下的形式

s.tX-Y=0,

根据最优性条件,它可以写成变分不等式的形式来求解.在实验中，我们取H=5I,γ=1.5,R=S=5,初始条件X=Y=λ=0,ε=10-5,文献[8][10]中的算法我们分别称为IPADM和PSM 计算结果如下

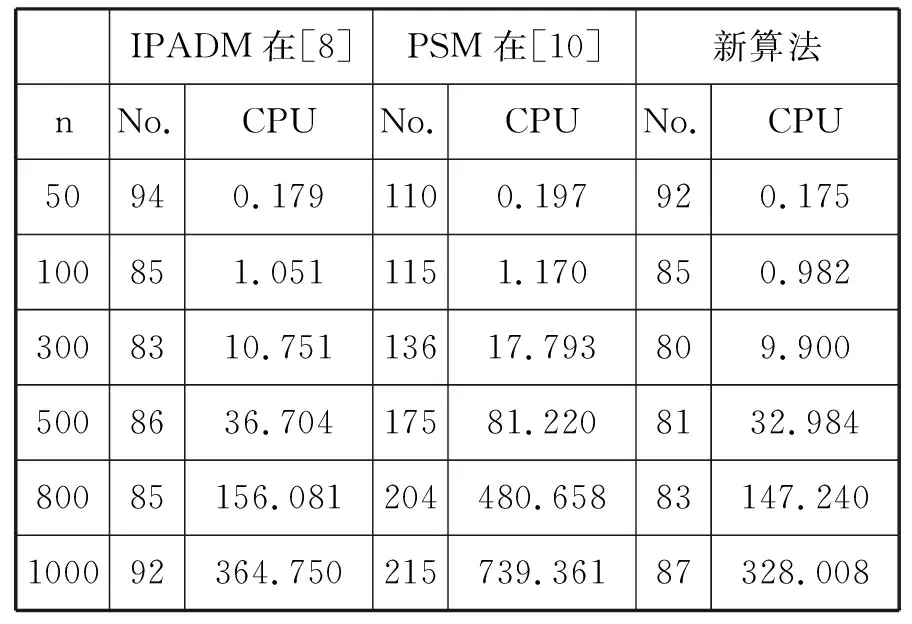
IPADM在[8]PSM在[10]新算法nNo.CPUNo.CPUNo.CPU50940.1791100.197920.175100851.0511151.170850.9823008310.75113617.793809.9005008636.70417581.2208132.98480085156.081204480.65883147.240100092364.750215739.36187328.008

5 结论

本文所证明的算法和文献[8]的区别在于子问题(15)-(17)的求解可以同时进行，而和文献[10]的区别在于它在求解子问题(15)-(17)时加入了渐近项,结合了交替方向法和邻近点分解算法的优点,且新算法同样适合并行计算,并得到了新算法的下降方向和最优步长.如何利用这种新的分解算法的优点来设计混合算法是需要进一步研究的问题.