排队论在食堂窗口服务中的应用

任娟娟（西南交通大学，四川 成都 611756）



排队论在食堂窗口服务中的应用

任娟娟
（西南交通大学，四川 成都 611756）

摘 要：本篇文章通过分析学校食堂窗口的排队系统这样一个实例，应用排队论，为学校食堂窗口服务构建相应的定量模型。通过建立数学模型，利用排队论中的相关知识结合 MATLAB软件求得了合适的窗口数，然后再结合实际分析食堂的利益，在两者之间进行权衡，得到了窗口数量的最优解。

关键词：排队论；数学建模；MATLAB；最优解

合适的窗口数量关乎学生和食堂管理者的利益。在这篇论文中，笔者通过分析我校某食堂窗口的排队系统，应用排队论为我校某食堂窗口服务构建相应的定量模型。

1　排队系统的分析

1.1排队系统基本排队过程

图1　排队系统框图

1.2稳定状态

为了分析的简便，我们假设输入过程和服务时间是平稳的。

（1）常用的数量指标。队长和排队长，等待时间和逗留时间，忙期和闲期。

（2）主要数量指标：平均队长；平均等待队长；平均逗留时间；平均等待时间。

（3）其他常用数量指标：窗口数目；平均到达率；到达的平均间隔；平均打饭速率；平均打饭时间；任一时刻稳态系统中所有学生数；在稳态系统中任一学生的逗留时间；在稳态系统中任一学生的等待时间；任一时刻稳态系统中状态为n的稳态概率；服务强度。

2　实例分析

2.1问题的提出

在我校，到饭点时，食堂排起长队变得十分拥挤。窗口的数量关乎学生和食堂管理者的利益，所以窗口的数量是大家都很关心的问题。因此我们要找到最合适的窗口数量。

2.2模型的假设

（1）假设学生在吃饭的高峰期到达人数是有限的，以泊松过程到达（参数为λ）；（2）学生对任意窗口没有偏好，打饭时间服从负指数分布（参数为μ）；（3）假设每个窗口有一个队列且没有插队现象。

2.3模型的建立及求解

这个模型符合排队论中的M/M/S模型。经过调查以及画概率直方图的方法，可判断出学生流符合泊松分布流。该食堂有5个窗口，下表显示某周周一到周五 11:30-12:30吃饭高峰期学生流的分布情况，每5分钟为一个时段到达。

表1　每5分钟学生到达人数统计表

由上表可知：

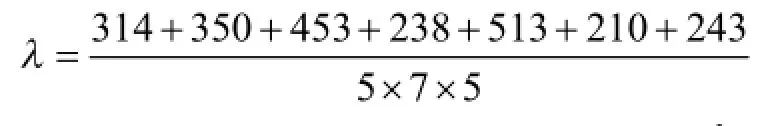
食堂中学生个数为0的概率：

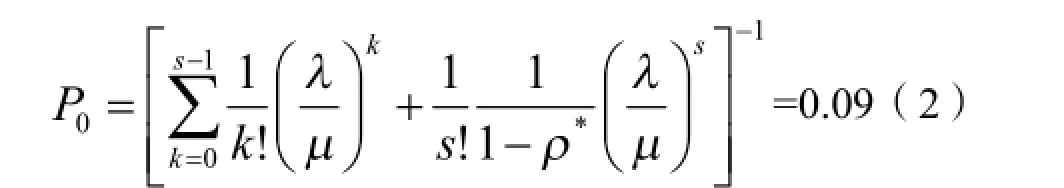
学生的平均等待队长为：

从上面数据可知，在吃饭高峰期来到食堂吃饭将会看到36个人都在买饭，其中32人在排队等待，每个窗口就有6个人在等待，平均要等待2.3分钟，要呆2.6分钟左右才能吃上饭。

2.4问题的分析

通过分析3中公式我们可以看出来窗口数量是影响平均排队时间的唯一因素。下面就对S的值对 W的影响进行分析，我把λ、μ还有不同的窗口数量代入公式（1）中，得到相应的ρ*的值，然后把λ、μ、s和ρ*代入公式（2）中得到 P0，［2］把上述步骤得到的数据代入公式（3）得到 Lq，进而得到相应的L、Wq和W的值，由上述运算过程我们得到了下表：

表2　学生平均逗留时间与窗口数量的关系表

用MATLAB7.0进行三次多项式的拟合，从而得到拟合图。拟合多项式关系式为：

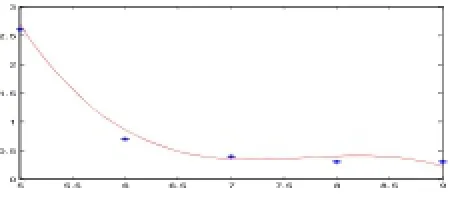
图2　w与s的关系的拟合图

从上图看出随窗口数量的增加，平均排队等待时间减少，当窗口数为7时，时间趋于平稳。经过调查综合多方面分析我们知道每增加一个窗口食堂的成本每周得增加300元。我们假定每五分钟可赚15元，由此得到：食堂因学生等待而损失了：C=15×2421W 。食堂因窗口数由6变为7可减少损失：ΔC=15×2421×0.3=10894.5。因此，最佳窗口数量为7。

3　模型的进一步讨论

上文分析中我们得到食堂的综合效益是由食堂的经济收益和社会效益来决定的。并且食堂的经济收益是由食堂的收入决定的，社会效益是由学生对食堂的服务满意度决定的（满意度是由学生在食堂的逗留时间决定的）。因此，在这里设食堂的收入为x，学生逗留时间为T，应用构造效用函数的方法并且赋予食堂收入所占的权重为ω，因此，食堂的经济收益可用来表示，社会效益可以用来表示，这样就得到了两个0到1之间的数据。由上述分析，得到：食堂的综合效益=食堂的经济收益+社会效益。我利用这个等式分析得出最佳窗口数量为 7，当窗口数为7是即可以缩短排队时间使得学生受益，也可以增加食堂收入，使双方都受益。

参考文献：

［1］陈传赉. 排队论.［M］. 北京: 北京邮电学院出版社， 1994.

［2］王兴贵， 焦争昌.基于排队论的银行排队问题研究［J］. 湘潭师范学院学报（社会科学版）， 2008（1）:58-60.

（责任编辑：雷 君）

中图分类号：F224.34

文献标识码：A

doi:10.3969/j.issn.1672-7304.2016.01.057

文章编号：1672–7304（2016）01–0120–02

作者简介：任娟娟（1989-）， 女，河南洛阳人 ，硕士研究生在读，研究方向：应用数学。

Applications Of Queuing Theory In Dining Room

REN Juan-juan
（Southwest Jiao tong University， Chengdu Sichuan 611756）

Abstract:This article， through the analysis of the school cafeteria window queuing system such a examples， the application of queuing theory and corresponding quantitative model is built for the school canteen service window. Through the establishment of mathematical model， using queuing theory knowledge combined with MATLAB software was used to derive the appropriate number of windows， and then combined with the actual analysis of the canteen of interests， in between trade-off optimal number of window are obtained.

Keywords:Queuing theory；Mathematical modeling；MATLAB software；Optimal solution