大型超市前端收银排班优化策略

綦小刚　丁小东

摘 要：论文首先通过排队论计算出超市在营业期间各时段来客数相对应的最优的需要开放的收银台的数量，然后根据排班的约束条件线性规划求解出不同班次的人员安排，并对某公司旗下的几个大型超市的真实数据进行验证，最后阐述了该优化策略的优越性和局限性。

关键词：排队论；线性规划；排班优化

一、引言

大多数顾客在大型超市（Hypermarket）购物时唯一能够感受到服务的地点就是收银台，在这种感受当中最强烈的就是对排队时等候时间的感受。根据心理学研究：一个人在超市等候时间超过7分钟，就明显感到情绪急躁起来。对超市来讲，如果开放的收银台不够，就造成过度排队等候；如果开放过多的收银台，又造成公司资源的浪费。

本论文研究的目的是要实现系统优化，保证服务、降低损耗。由于保证服务（顾客要求）与降低服务强度（收银台要求）是相互矛盾的，因而最终的评价要借助于经济性指标，即让顾客等待引起的损失与服务工作发生费用之和最小。从实际工作来看，这一标准也是十分有意义的，因为提供服务者与被服务者的利益往往有很大的关联性：即服务质量越高，顾客就越多，利润也越高，这在大型超市中有更显著地体现。

二、基于排队论的收银台最优开放数量模型

1.模型的建立和分析

大型超市顾客的到来基本是随机的，因此认为超市收银系统服务是一个典型的随机服务系统。当系统运行较长时间达到稳态后，系统的情况按实际总结如下：

（1）排队结构是多队多服务台结果如（图1），系统有c个平行的收银台1，每个收银台的服务时间是一个随机变量，服从参数为μ的负指数分布。

（2）顾客的到达时间符合非时间齐次泊松过程（Non-homogene-

ous Position Process）到达速率是λ（t）。顾客在不同时间段的到达速率不同，但在某一时间段内到达速率是固定的，即在某一时间段内顾客的到达时间服从参数为λ的泊松过程。2

（3）系统中如顾客数大于收银台数，则不会有空闲的收银台，进入系统的顾客可随时改变其队列。

（4）到达过程、服务过程和各个服务过程之间都是相互独立的。

（5）假设系统的等待位置为∞，服务规则是先来先服务即FC-

FS。

假如超市规定各收银排队人数不超过5人，顾客在收银台排队系统中的平均等待时间不超过7分钟，则c应该满足条件：

2.模型的编程实现

该程序在数学优化建模软件LINGO 11.0中测试通过。我们以某门店在某个星期日7：00～8：00时段为例，运行结果为：此时段最优开放的收银台数是3台。程序如下：

min=c；

T=1.26； ！汇总统计收银员平均客流算术平均值得出μ=47.62117人次/小时，所以收银员的服务时间服从T=60分钟/μ=1.26分钟/人的负指数分布；

R=1.55； ！根据公司IT系统导出得到在该时段顾客到达速率λ的值为R=1.55人/分钟；

a=R*T； ！由a=λ/μ推导出；

a/c<1； ！排队系统中服务员的利用率为ρ=a/c<1；

L_q<=5；W_q<=7；

P_wait=@peb（a，c）；

W_q=P_wait*T/（c-a）；

L_q=（a/c）/（c-a）*P_wait；

@gin（c）；

三、规划求解最优排班模型

得出每时段的最优开放的收银台之后，接下来我们共同探讨一下如何通过线性规划求解计算出最优的排班收银员人数。

1.模型的建立和分析

（1）线性规划模型的建立，如图2。模型介绍：

①来客数时段分解：把超市营业时间按小时划分。

②当班工时：汇总超市门店的每个班次的累计工时数，“0”表示用餐状态或下班状态。

③当班人数：表示每个班次安排的收银人数总和。

④班次：超市门店的班次。例如：7-16表示上班时间从7：00～16：00。

⑤理论收银台最优开放数：通过LINGO编程计算出每个来客时段的理论收银台最优开放数。

⑥排班最优人数：表示某一小时的时段内，各班次收银员人数之和。例如9点～10点期间排班最优人数为：

X3=Y1*1+Y2*1+Y3*1+Y4*0+Y5*0

⑦浪费工时：通过“排班最优人数”减去“理论收银台最优开放数”的值，来评估实际排班的人数与理论收银台最优开放数之间的差距。正数表示开放的收银台偏多，负数表示开放的收银台不足以应对当前的客流量。

（2）模型的约束条件分析

决策变量、目标函数、约束函数三种信息的单元格区域为：

①决策变量：在C19～G19单元格中（即当班人数）；

②目标函数：在I19单元格中（即全天总工时）；

③约束函数在第I3～I17行。约束函数主要是确保“排班最优人数”不小于“理论收银台最优开放数”，约束条件如下：

X1，即I3=SUMPRODUCT（C3：G3，C19：G19）≥H3

X2，即I4=SUMPRODUCT（C4：G4，C19：G19）≥H4

......

X15，即I15=SUMPRODUCT（C17：G17，C19：G19）≥H17

（3）线性规划求解

“线性规划”是Excel系统中的较少用到的一个宏，需要进行加载才能运行。把模型的约束条件录入到规划求解参数中去，最优配置结果将会显示在目标单元格中。如图3

四、数据验证

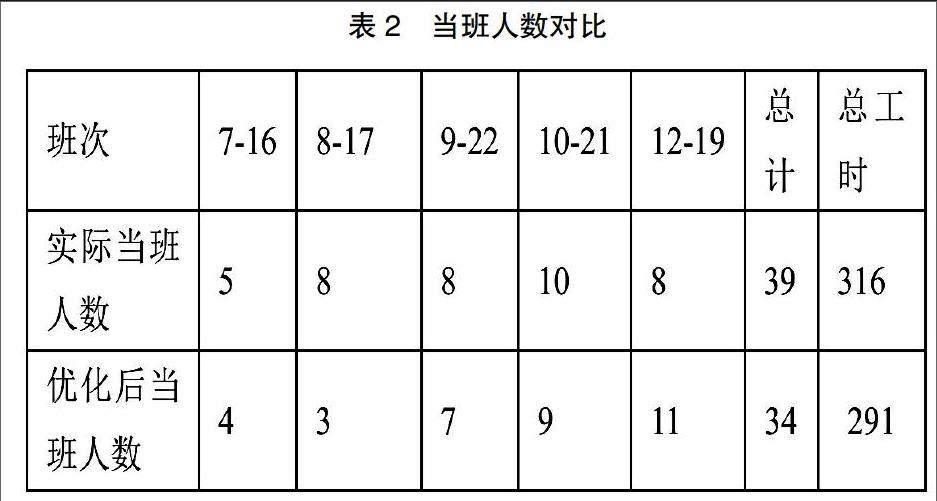
我们以某门店在2015年12月20日星期日的数据为例。当天来客数为11917人。该门店的当日耗用的总工时是316个小时，当班的收银员39人。

1.验证最优开放的收银台数量

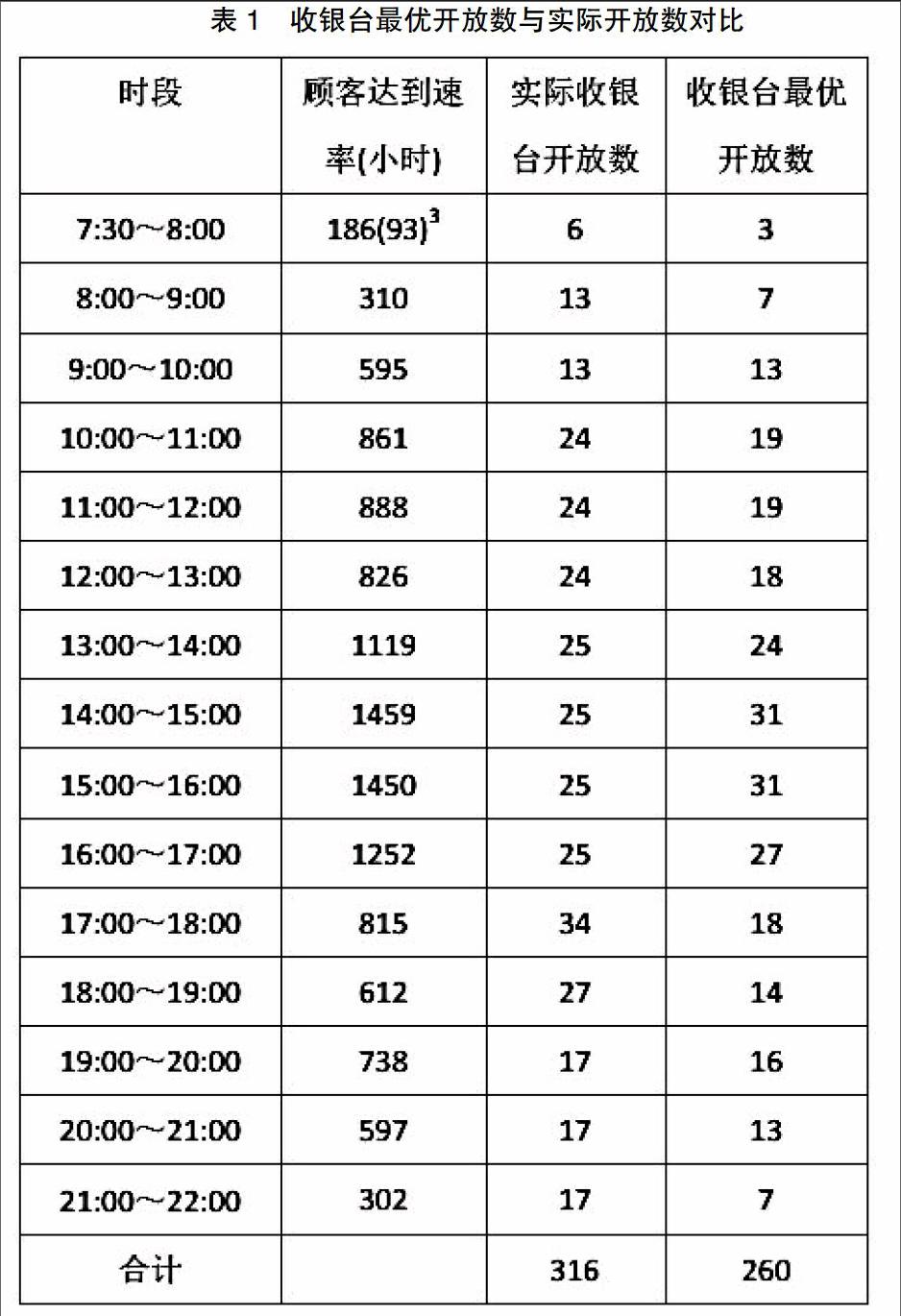
汇总统计收银员平均客流量算术平均值之后得到收银员当日的服务时间为47.62117人次/小时，其负指数分布为1.26min/人次。每时段的顾客到达数是从公司IT系统中导出，详见表1。通过Lingo可分别计算出每汇总统小时收银台最优开放数。

结论：当日14点之前和17点之后开放的收银台偏多，营业期间两端时段开放的收银台浪费率4甚至多达100%，而在当日14：00～17：00这3个小时的高峰期间开放的收银台又偏少。

2.验证最优排班人数

我们结合现场当班人数来对比线性规划模型优化的排班人数。结合图3计算结果得出表2。

结论：最优解的全天当班总人数由原来的39人下降到34人，全天总工时由原来的316小时降低到291小时，最终节约了5个人工，25个工时。

五、结语

本论文研究的目的虽然是实现系统优化，但并不仅仅是为了精简员工，而是通过优化提高管理效率，把现代企业管理意识植入到超市管理当中，逐渐建立起一个科学化的管理机制。

1.模型的优势

（1）负责排班的前端主管可以利用模型，根据季节不同、来客数时段峰值的变化而设计班次及最优人数，也可以验证排班的合理性。

（2）该优化策略具有灵活的可操作性。例如：门店因为人员短缺，则可以去除此时段的约束条件，即允许“浪费时间”字段是负数的情况，这相当于人为修正来客流曲线从而实现更优化、更具有现实意义的排班策略。

（3）该模型不仅考虑到了换班吃饭的问题，甚至还可以外延“班次”字段的定义，即让班次对应到每个收银员。

（4）模型把来客数按时段分解，通过与“理论收银台最优开放数”的对比，使前端领班或主管能对当前收银员应对来客数的承载量进行预估，为其现场管理提供了便利，同时也为前端领班或主管的管理能力的评估提供了量化的手段。

（5）模型也可以在连锁门店之间横向对比其前端的收银现状，从而形成良性的水平竞争局面，提供结构性的管理数据。如案例中的门店服务效率近期总体在45～50人/小时之间，同比另一门店B高达60～65人/小时之间，而门店C只有30～35人/小时之间。显而易见，门店B的收银员多为熟手或业务熟练度较高，门店C的收银员多为新手或业务熟练度较低。

2.模型的不足和改善

（1）优化在提高人力资源使用效率的同时，也降低应对突发情况的能力。当现场发生断电、个别收银员突发性旷工等情况时，将难以应对，实际应用要考虑增加一定比例的弹性。

（2）模型仅仅考虑到收银工作本身，现实中在收银员当班期间，除了收银的工作，还有开关店、收银台侧架的补货、清洁、现金清点等工作。建议合理利用"浪费工时"字段中数据，来安排收银以外的相关工作，更能提高效率。

（3）模型中的客流高峰仅仅细分到以小时数为基数单位，有时客流会集中在更细分的时间段，造成瞬时拥堵，这种现象在某些特殊时段甚至是常态。例如在21：00～22：00超市营业的最后时段，通常会出现100多位顾客集中在21：30～21：45时段买单。要解决这一问题，必须采用其他方案解决。

（4）在最优服务和最优效率之间平衡的问题。这两者的矛盾在于：顾客的来客流是非对称、非平滑的曲线，有些时刻的曲线是突兀的；同时，不可能安排收银员上班一、二个小时之后就要求其下班，也要考虑人性化管理的问题。

注释：

①每个收银台对应一个收银员

②符合以下四个性质的顾客流称为泊松流又称最简单流。

a.流的平稳性。在时间区间[t，t+△t]内到达k位顾客的概率与t无关，只与△t有关。

b.流的无后效性（独立性）。顾客的到来是不相关联的，或称为相互独立的。在两个互不交叉时段τ1和τ2内，来到系统的顾客数是相互独立的。

c.流的普通性。在足够小（充分小）的时间间隔内，或称为“同一瞬间”，正好有两个或两个以上顾客来到系统的概率为高阶无穷小，可以忽略。

d.流的有限性。在任意的有限时间区间内，到达有限位顾客的概率为1。换言之，有0个顾客至有k个顾客（k→∞）这些情况中，必定有一种要发生。

③该超市实际是从早上七点半开始营业，所以半小时内来客数是93，则每小时客流是186。

④有些大型超市中，还存在卖场内的单独收银机、出口换购等收银台，统计时需要除去这些收银员占据的工时，也要除去这些收银台承载的客流数，本案例中已经去除。

参考文献：

[1]苏兆龙.排队论基础[M].成都：成都科技大学出版社，1998.

[2]孙昌言，陈伟忠.工商管理中的定量分析方法[M].上海：同济大学出版社，2003.

作者简介：綦小刚（1977- ），男，上海，曾任卜蜂莲花某门店副店，同济大学2010级MBA；丁小东（1981- ），男，上海，曾任卜蜂莲花某门店副店，华东理工大学2009级MBA