多元回归模型在物流需求分析中的应用

李 勇（安徽财经大学，安徽 蚌埠 233000）



多元回归模型在物流需求分析中的应用

李 勇
（安徽财经大学，安徽 蚌埠 233000）

摘 要：物流需求分析是物流设计与规划的重要内容，本文对物流需求分析等方面的理论和方法进行了简要的总结和介绍，并重点介绍多元回归模型在物流需求分析的应用。

关键词：物流需求分析；方法；多元回归模型

物流需求分析是指将物流需求与生产需求的社会经济活动进行相关分析的过程，物流作为服务性行业，与生产、流通、消费等整个社会经济活动息息相关，是社会经济活动的重要组成部分。［1］所以，物流需求分析与社会经济发展有密切相关性，社会经济发展是影响物流需求的主要因素。

1　物流需求分析的主要方法

物流需求分析是基于物流数据的基础上，利用一定的科学方法对物流需求的变化和发展趋势进行的预测。物流需求预测的方法基本上可以划分为定性预测法与定量预测法两大类［2］。

2　多元回归预测法

多元线性回归是研究一个因变量与两个或两个以上自变量的回归，描述因变量y如何依赖于自变量x1，x2，…，xk和误差项ε的方程，称为多元回归模型。是反映一种现象或事物的数量以多种现象或事物的数量的变动而相应地变动规律。

2.1回归模型

涉及 k 个自变量的多元回归模型可表示为：

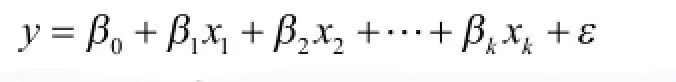
（1）β0 ，β1，β2 ，…，βk是参数，也称偏回归系数；（2）βi表示假定其他变量不变，当xi每变动一个单位时，y 的平均变动值；（3）ε是被称为误差项的随机变量，包含在y里面但不能被k个自变量的线性关系所解释的变异性。

ε基本假定：（1）误差项ε是一个期望值为0的随机变量，即 E（ε）=0；（2）对于自变量 x1，x2，…，xk的所有值，ε的方差σ2都相同；（3）误差项 ε是一个服从正态分布的随机变量，即ε～N（0，σ2），且相互独立。

2.2估计的多元回归方程

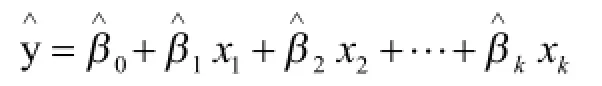
2.3参数由最小二乘法估计

最小二乘法是通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使这些求得的数据与实际数据之间误差的平方和为最小。使因变量的观察值与估计值之间的离差平方和达到最小来求得。

2.4多重判定系数

多重判定系数R2指回归平方和占总平方和的比例，反映因变量y取值的变差中，能被估计的多元回归方程所解释的比例。

2.5估计标准误差

估计标准误差是说明实际值与其估计值之间相对偏离程度的指标，估计标准误差的值越小，则估计量与其真实值的近似误差越小。

2.6显著性检验

线性关系检验是检验因变量与所有自变量之间的线性关系是否显著，检验方法是将回归均方（MSR）同残差均方（MSE）加以比较，应用 F检验来分析二者之间的差别是否显著，如果是显著的，因变量与自变量之间存在线性关系如果不显著，因变量与自变量之间不存在线性关系。

2.7回归系数的检验

当线性关系检验通过后，对各个回归系数有选择地进行一次或多次检验，究竟要对哪几个回归系数进行检验，通常需要在建立模型之前作出决定，对回归系数检验的个数进行限制，以避免犯过多的第Ⅰ类错误（弃真错误），对每一个自变量都要单独进行检验，应用t 检验统计量。

3　物流需求预测回归模型

由于受统计数据可获得性约束，在对广西省物流需求规模进行预测时选择“货物运输量”为衡量指标。以国内生产总值、第一产业产值、第二产业产值、第三产业产值、零售总额、外贸总额为自变量。利用SPSS软件对物流统计数据进行相关性分析，采用逐步回归的方法得到表2可以看出判定系数为0.983，说明自变量对因变量的解释程度很高。

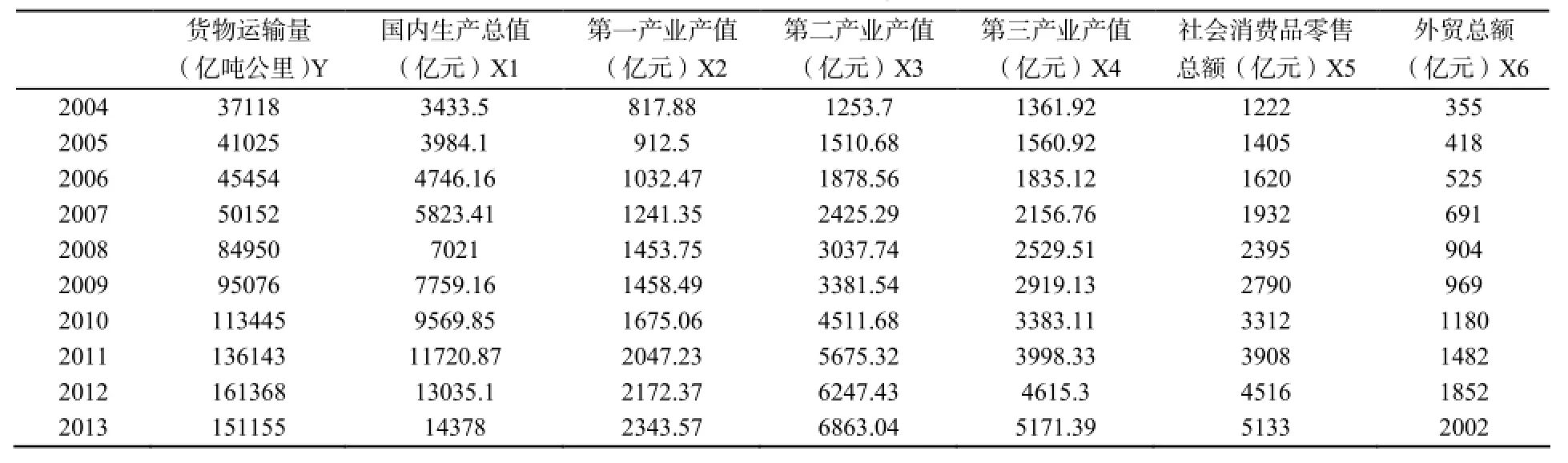
表1　2004-2013年广西壮族自治区物流统计数据

通过表可以看出回归模型为 y=7193.264+ 22.943 X3，并且显著。回归模型中表示货物运输量的增加多是由广西区内第二产业发展引起的。

表2　模型汇总

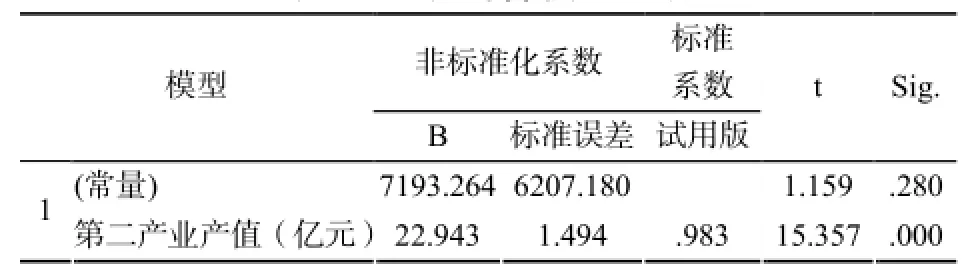
表3　回归计算模型系数

表4　回归值与实际值的比较

4　结论

物流需求分析是物流决策的重要依据，本文提出的物流需求回归模型融合了几种经济指标，较好地将物流需求与社会经济发展紧密的联系在一起，使物流需求分析过程很好的把握经济与物流的关系，因而具有较高的应用价值。

参考文献：

［1］杨荣英，张辉，苗张木.物流预测技术中的移动平均线方法［J］.武汉理工大学学报（交通科学与工程版 ），2001（3）：353-355

［2］孙莹.区域物流规划——理论、方法及应用［M］.北京：冶金工业出版社，2012.

［3］徐杰、鞠颂东.区域经济的发展对地区物流需求的影响一长江经济区发展对安徽地区物流需求影响的实证分析［J］.数量经济技术经济研究，2003（4）:130-133.

（责任编辑：廖建勇）

中图分类号：F252.21

文献标识码：A

doi:10.3969/j.issn.1672-7304.2016.01.054

文章编号：1672–7304（2016）01–0114–02

作者简介：李勇（1963-），男，安徽蚌埠人，副教授，研究方向：信息与计算科学专业。

Application of multiple regression model in logistics demand analysis

LI Yong
（Anhui Finance and Economics University， Bengbu Anhui 233000）

Abstract:Logistics demand analysis an important content of logistics design and planning， the theoryand method of logistics demand analysis are summarized and introduced， and focuses on the application of multiple regression analysis model in logistics demand.

Keywords:Logistics demand analysis； method； multiple regression model