高等代数中的几类数学思想方法

姚裕丰

（上海海事大学文理学院，上海201306）



高等代数中的几类数学思想方法

姚裕丰

（上海海事大学文理学院，上海201306）

摘要：数学思想方法是数学知识的精髓和核心，研究数学思想方法对培养学生的数学能力的积极促进作用.结合高等代数的教学实践，介绍了高等代数中类比、举反例、几何、变换及构造等几种数学思想与数学方法，通过具体的实例说明了这些思想方法在高等代数中的应用.

关键词：高等代数；类比；举反例；几何；变换；构造

高等代数是数学类专业最重要的基础课程之一，是学生学好后续更为深入的数学课程的基础［1-7］.高等代数具有高度的抽象性和严谨的逻辑性等特点，与学生原有中学的认知结构有较大的差别，致使学生普遍认为学习高等代数很困难.本文结合教学实际以及具体的实例，探讨了高等代数中的几类重要数学思想方法的应用，以提高教学效果和质量.

1　类比的思想方法

类比方法是指根据两个不同的事物在某些方面的相似之处，猜测这两个事物在其他方面也可能有类似之处，从而作出某种判断的方法.类比方法是科学研究开拓创新的重要手段.数学中有很多概念和结论都是用类比推理得出的［8-10］.

在高等代数教学中，恰当地选择类比对象，通过类比，可以引导学生利用已有的中学数学知识理解和掌握高等代数中的相关概念和性质，这样学生易于接受，不会感到难懂.如在讲解数域F上的一元多项式环F［x］的整除理论时，可以用整数环的整除理论来类比.学生熟悉整数的带余除法、整除、最大公因数和最小公倍数等概念，相应地可以类比引出一元多项式环F［x］中的相应概念和性质.在整数中，素数起了很重要的作用，是整数的“基石”.在一元多项式环F［x］中，相应的“基石”称为不可约多项式.素数p具有性质：若p|ab，则p|a或者p|b.相应地，在一元多项式环F［x］中也有类似的性质：设p（x）是不可约多项式，如果p（x）f（x）g（x），则p（x）f（x）或者p（x）g（x）.在整数中，任一个大于1的正整数都可以分解为素数的乘积.相应地，在一元多项式环F［ x］中也有因式分解定理，即任一个多项式都可以分解为不可约多项式的乘积.

2　　举反例的思想方法

从科学性来讲，反例是推翻错误命题的有效手段.从教学上而言，反例能够加深学生对正确结论的全面理解.举出恰当的反例能帮助学生加深理解和掌握数学概念，正确地应用相应的数学定理.在高等代数教学中可以通过培养学生举反例的思想以提高他们分析和解决问题的能力，正确理解和把握数学概念［11］.

例1若不可约多项式p（x）是f（x）的k重因式，则p（x）是f'（x）的k-1重因式.反之未必正确.即若不可约多项式p（x）是f'（x）的k-1重因式，p（x）未必是f（x）的k重因式.

反例，设f（x）=x4+1，p（x）=x，则p（x）是f'（x）的3重因式，但p（x）不是f（x）的因式.进一步可以证明，若不可约多项式p（x）是f'（x）的k-1重因式，且p（x）是f（x）的因式，则p（x）是f（x）的k重因式.

例2本原多项式不一定是不可约多项式.

反例，设f（x）=x3+x2+x+1，则f（x）是本原多项式，但f（x）=（x2+1）（x+1）是可约多项式.例3正交矩阵的行列式为1或者-1，但反之不真.

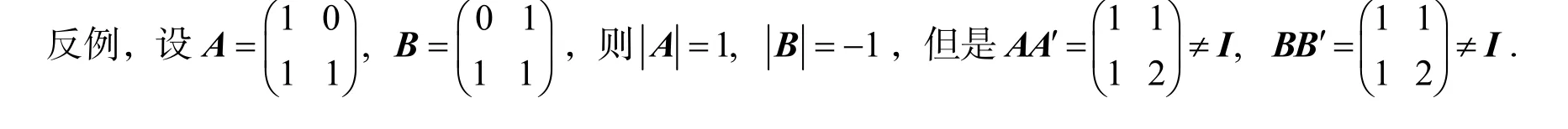
3　几何思想方法

高等代数中很多概念极具抽象性，如果能找到恰当的几何例子，通过几何直观的思想方法［12-13］，可以帮助理解抽象难懂的概念，从而达到事半功倍的效果，提高学生学习的积极性和自信心.

3.1线性空间概念的教学

线性空间概念是公理化定义的，是指这样一个集合，在这个集合上定义了2种运算“加法”和“数乘”，并且满足8条性质.线性空间的概念对于初学者来说非常抽象，教师可以将中学学过的数轴上所有点的全体作为例子，“加法”和“数乘”2种运算就是通常的实数加法和乘法，可以很容易验证线性空间定义中的8条性质都满足，它们是实数的基本性质.进一步，以二维平面以及现实生活中的三维空间为例，其中的“加法”和“数乘”2种运算即为向量的加法和数乘，很容易验证线性空间定义中的8条性质都满足.

3.2矩阵中的几何

矩阵可视为行向量组或列向量组，这样，作为代数对象的矩阵赋予了几何意义，可以把有关矩阵关系式的问题转化为向量的关系式，从而可以通过向量的几何性质找出矩阵的一些性质.

例4设A，B为2个n阶方阵，且AB=0 .则rank（A）+rank（B）≤n.进一步，若存在常数a，b，使得aA+bB可逆，则rank（A）+rank（B）=n.

证明设A=（α1，α2，…，αn），B=（β1，β2，…，βn），其中：αi，βj均为列向量.则rank（A），rank（B）分别为向量组α1，α2，…，αn以及β1，β2，…，βn的秩.由于AB=0，故Aβi=0（1≤i≤n）.

从而齐次线性方程组AX=0的解空间维数不小于rank（B）.而由线性方程组解的一般理论可知，齐次线性方程组AX=0的解空间维数为n-rank（A），故n-rank（A）≥rank（B）.因此rank（A）+rank（B）≤n.

设aA+ b B可逆.如果rank（A）+rank（B）＜n，则向量组α1，α2，…，αn，β1，β2，…，βn的秩小于n.由于aA+bB=（aα1+bβ1，aα2+bβ2，…，aαn+bβn），从而rank（aA+bB）＜n，这与aA+ b B可逆矛盾，故rank（A）+rank（B）=n.

4　变换的思想方法

变换是将复杂问题化为简单问题，抽象问题化为具体问题，困难问题化为容易问题的等价思想方法，是高等代数中常用的技巧［14-15］.如将线性方程组的问题转化为用增广矩阵来描述，从而对线性方程组解的讨论等价地转化为增广矩阵标准型的讨论，根据增广矩阵标准型的情况得到原方程组解的情况.在矩阵中，有各种诸如合同、相似等标准型.利用矩阵的初等变换可以求解线性方程组、矩阵的秩和逆矩阵等.

5　构造的思想方法

构造法可用来对数学概念和结论进行构造性解释，表现出数学思维的试探性和创造性.应用构造法需要对问题有充分的把握和理解，挖掘其内蕴的本质.构造法在高等代数中有广泛的应用，有大量的结论是通过具体构造给出的.

例5设V是数域P上的n维线性空间.证明：存在V的无限子集W，使得W中任意n个向量都线性无关.

证明取V的一组基α1，α2，…，αn，对于任意.

例6证明任一个秩为r的矩阵都可以表示为r个秩为1的矩阵之和.

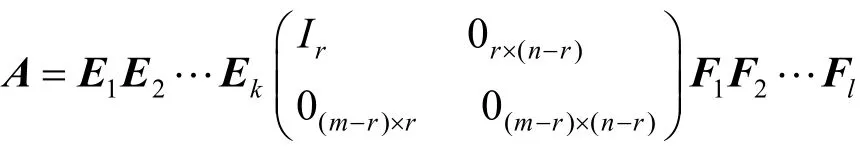
高等代数中蕴含了丰富的数学思想方法，教师要充分挖掘和归纳，使学生理解和掌握这些数学思想和数学方法，从而提高教学质量和教学效果.

参考文献：

［1］张禾瑞，郝炳新.高等代数［M］.北京：人民教育出版社，1986

［2］北京大学数学系.高等代数［M］.北京：高等教育出版社，1988

［3］丘维声.高等代数［M］.北京：高等教育出版社，2002

［4］刘仲奎，杨永保.高等代数［M］.北京：高等教育出版社，2003

［5］姚慕生，吴泉水.高等代数学［M］.上海：复旦大学出版社，2008

［6］施武杰，戴桂生.高等代数［M］.北京：高等教育出版社，2009

［7］黄庭祝.高等代数［M］.北京：高等教育出版社，2012

［8］仲秀英.波利亚的类比思想与数学课程改革［J］.重庆师范大学学报：自然科学版，2003，20（3）：84-86［9］周海芳.例谈类比思想在数学教学中的应用［J］.宿州教育学院学报，2001（4）：94-95

［10］肇慧，焦艳会，任中贵.比较教学法在代数教学中的应用［J］.高师理科学刊，2012，32（6）：82

［11］刘向华.反例在教学中的作用［J］.数学理论与应用，2001（4）：82-85

［12］范志勇，毋光先，白海英.高等代数中的几何直观方法［J］.廊坊师范学院学报：自然科学版，2010，10（4）：10-12

［13］王瑞卿.高等代数的几何直观化教学［J］.高师理科学刊，2014，34（1）：94-96

［14］魏平.初等变换在高等代数中的应用研究［J］.数学教学研究，2010（2）：49-53

［15］王文省，姚忠平，钟红心.初等变换的思想方法在高等代数中的应用［J］.聊城师院学报：自然科学版，2000（3）：76-78

Discussion on several mathematical thought and methods in advanced algebra

YAO Yu-feng
（School of Arts and Science，Shanghai Maritime University，Shanghai 201306，China）

Abstract：Mathematical thought and methods are the soul and core of mathematical knowledge. The study of mathematical thought and methods will play an active role in the cultivation of students′mathematical ability.Associated with actual experience in the teaching of advanced algebra，introduced several mathematical thought and methods，such as，analogy，counterexample，geometry，transformation，construction etc.Some concrete examples were given to demonstrate how to apply these thought and methods in advanced algebra.

Key words：advanced algebra；analogy；counterexample；geometry；transformation；construction

中图分类号：O151∶G642.0

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.018

文章编号：1007-9831（2016）05-0062-04

收稿日期：2016-03-01

基金项目：上海海事大学教师教学激励计划项目；上海海事大学“高等代数”重点课程项目

作者简介：姚裕丰（1982-），男，江西峡江人，副教授，博士，从事代数学研究.E-mail：yfyao@shmtu.edu.cn