双重向量积定理的一个新证法

吕振环，惠淑荣，张阚，丰雪

（沈阳农业大学理学院，辽宁沈阳110866）

孙秀娟1，金民锁2，王新霞1



双重向量积定理的一个新证法

吕振环，惠淑荣，张阚，丰雪

（沈阳农业大学理学院，辽宁沈阳110866）

摘要：在解析几何中，双重向量积是向量的一种运算，但它的证明方法都比较复杂.给出双重向量积定理的一种新的证明方法，相对其他证法，该证明方法更加简洁、易懂.

关键词：双重向量积；线性表示；数量积

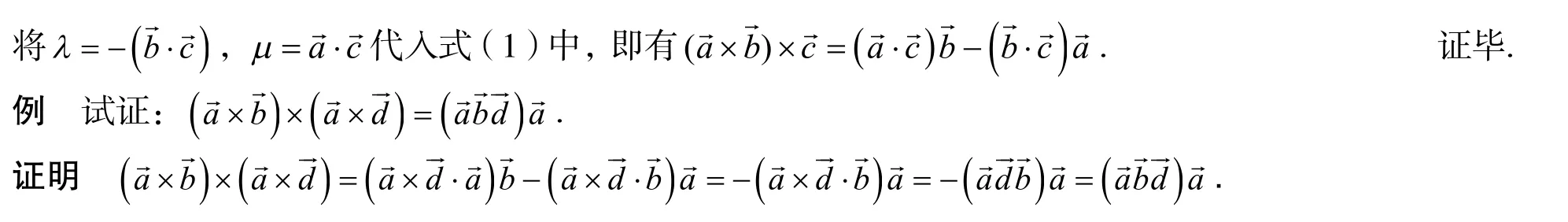
参考文献：

［1］吕林根，许子道.解析几何［M］.4版.北京：高等教育出版社，2006

［2］李养成.空间解析几何［M］.北京：科学出版社，2007

［3］刘桂仙，胡贵新.双重向量积公式的一种证明方法［J］.高师理科学刊，2013，33（5）：9-10

［4］鲁春铭，丰雪.线性代数［M］.北京：中国农业出版社，2013

一堂高等数学微课设计研究与实践

孙秀娟1，金民锁2，王新霞1

微课程并不是指为微型教学而开发的微内容，而是运用建构主义方法化成的、以在线学习或移动学习为目的的实际教学内容［1］.微课程现在作为一种新兴的学习方式，它主要指适用于教育教学中的短而精的视频课程.

1　高等数学微课教学选题

一次微课视频时间较短，要达到短时高效，就要恰当地选择知识点题目，选题要能够激发学生求知欲，实现师生互动，与多媒体课件有机结合.如对于高等数学上册的教学，教师可以选取数列极限的描述性定义、重要极限及其在求极限中的应用举例（如切线问题和速度问题等）、可微的概念、罗尔定理的应用、拉格朗日定理及其几何意义、曲率的概念等应用性较强的题目，根据知识点再选取一些实际案例［2］，用PPT软件进行课件制作，然后通过多媒体技术等软件制作视频.

2　高等数学微课教学过程

一般整个教学过程控制在10～15 min左右，甚至更短，但要完整地讲解出一个知识点或应用问题，要保证过程完整性.由实际问题引出微课课题，教师提出一些有针对性的未知问题，引发学生去思考，进入新知识点讲解，应用知识点解决所提出的问题，紧扣主题，最后简洁明了地总结本节微课教学内容，使学生明确本节课学习思路，巩固知识点应用.微课制作过程中可以插入图片、声音、短视频和音乐等，不局限于单一的PPT课件的应用，这样更能充分地吸引学生注意力.这种生动形象的教育方式的教学效果远远地超出了传统的单一语言教学的教学模式.

3　高等数学微课教学的实施

以高等数学上册可分离变量微分方程知识点讲解为例，给出本节微课设计及具体教学实施过程.

3.1教学背景（1）可分离变量微分方程的地位与作用.微分方程发展的古典时期，研究的主题是：尽可能设法把当时遇到的一些类型的微分方程求解问题化为积分（求原函数）问题，这类方法，习惯上称为初等积分法.初等积分法中，最基本而重要的就是分离变量法.可分离变量的微分方程是最简单、最基本的一类一阶微分方程，是求解齐次方程和可降阶的二阶微分方程等的基础.（2）教师的准备.教师通过互联网上“百度百科”、期刊文献等途径，对微分方程积累了一定的多媒体课件素材；课余阅读数学文化方面的书籍，积累一定量的将数学思想方法与数学文化融入课堂教学之中的经验.在分析和整合关于可分离变量微分方程的教学主体内容后，完成本节课的教学设计以及PPT制作.（3）教学方法.案例教学法与问题情境教学法相结合.（4）教学手段.通过多媒体动画、视频、图片与板书演示相结合录制成15 min左右视频教学.

3.2教学内容安排（1）运用核废料处理问题案例［3］，创设情境，引入课题；（2）分析探究，讲解可分离变量微分方程及其求解；（3）解决核废料处理问题案例，达到学以致用；（4）归纳总结，通过思考练习使学生掌握可分离变量微分方程解法及应用［4-5］.

3.3微课视频的录制与后期处理教师在录制视频前，准备好本节课教学设计，如教学背景了解、教学板书设计、教学内容PPT素材设计及教师的着装.只有做好录制前期工作才能保证录制视频的效果，要选择明亮的专门录播室录制，保证播放质量，后期可以用Camtasia Studio软件对录制的视频进行编辑视频、添加声音、PPT抠图、添加背景音乐、添加解说词和转场动画等技术制作，这就要求教师还要有一定的计算机软件技术基础.

［1］杨雯靖.基于微课的高等数学教学模式研究［J］.开封教育学院学报，2015，35（10）：118-119

［2］盛晟.微课的设计与制作［J］.计算机光盘软件与应用，2014（24）：263-264

［3］同济大学应用数学系.高等数学［M］.北京：高等教育出版社，2007：260-261

［4］李心灿.高等数学应用205例［M］.北京：高等教育出版社，1997：105-107

［5］孙秀娟，王新霞，王春.高等数学案例教学法［J］.高师理科学刊，2012，32（3）：88-89

（作者单位：黑龙江科技大学，1.理学院，2.信息网络中心，黑龙江哈尔滨150022）

A new proofing method for double cross product theorem

Lü ZHEN-huan，HUI Shu-rong，ZHANG Kan，FENG Xue
（School of Science，Shenyang Agricultural University，Shenyang 110866，China）

Key words：double cross product；linear expression；dot product

Abstract：In analytic geometry，double cross product is a arithmetic，its proof method are more complex.Given a new proof method for the double cross product theorem.It looks very simple and convenient compared with many other methods.

中图分类号：O182.2

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.002

文章编号：1007-9831（2016）05-0005-02

收稿日期：2015-12-30

作者简介：吕振环（1970-），女，辽宁沈阳人，副教授，硕士，从事数学教学及数学模型研究.E-mail：lvzhenhuan@163.com

基金项目：黑龙江省高等教育学会“十三五”期间教育科学研究规划课题；黑龙江科技大学教学研究项目