基于数值积分的传染病SIRS模型参数估计

宋丹丹，王晶囡，杨光旭，李佳思，杨嘉欣

（哈尔滨理工大学 应用科学学院，黑龙江 哈尔滨 150080）



基于数值积分的传染病SIRS模型参数估计

宋丹丹，王晶囡，杨光旭，李佳思，杨嘉欣

（哈尔滨理工大学 应用科学学院，黑龙江 哈尔滨 150080）

摘要：针对具有免疫的传染病SIRS模型，利用三次Hermite插值函数及数值积分公式，基于患病的各个种群人数估计值的误差最小原则，将参数估计问题转化为非约束优化问题.将数据带入后可得关于模型参数的多项式，为求得该式最小值，将其分别对各个参数进行微分，得到关于模型参数的非线性方程组.使用最速下降法获得较为合理与精确的初值，在该初值的基础上利用牛顿法对非线性方程组进行求解，得到了该模型的高精度参数估计值.并对计算结果进行数值仿真，数值仿真实验表明，所给出的参数估计方法能够较为精确地估计出相应参数值.

关键词：SIRS模型；数值积分；牛顿法；数值仿真；参数估计

对于各类新型突发传染病，人类对它的防治还处于初级阶段，如何有效地从宏观上了解和掌握这些流行病的传播规律，控制传染病的蔓延就显得尤为重要［1-8］.本文研究现实复杂情形下（包含非线性传染率，有隔离措施，群外个体迁入，生育与死亡以及疾病可以水平或者垂直传播等）SIRS传染病模型的参数估计问题.采用三次Hermite插值函数，得到具有五阶精度的数值积分公式，利用该公式对SIRS传染病模型进行离散化，将参数估计问题转化为无约束的优化问题，使用Matlab软件进行操作，最终得到估计误差最小的参数估计值.

1　SIRS传染病模型

在文献［1］的基础上，本文考虑了感染者具有免疫作用并对该文献中传染病模型进行适当删减，建立传染病模型其中：S= S（t），I= I（t），R= R（t）分别表示易感个体、染病个体（又分为未被隔离染病个体I1和隔离染病个体I2，即I= I1+ I2）和康复个体的数量；ε表示隔离率；β（N）表示传染病通过有效接触进行传播的传播系数；a表示接种比例；As表示易感个体的输入率；b表示自然生育率；d表示自然死亡率；d表示染病个体的死亡率；γ表示治愈率.初始条件为S（ t0）= S0，I1（ t0）= I10，I2（ t0）= I20，R（t0）= R0.As，a，b，c，d，β（N），ε，γ为待求参数.

2　三次Hermite插值多项式与数值积分

一般地，求三次Hermite插值函数要求给定x0，x1和相应的函数值F（x0），F（x1）以及微商值F'（x0），F'（x1） .

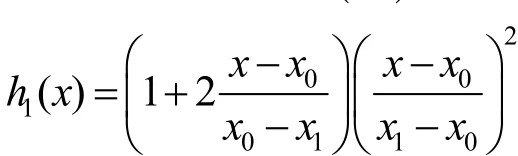
其中：ξ∈［x0，x1］.

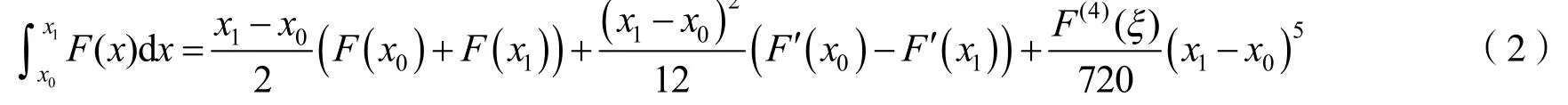
3　SIRS传染病模型的参数估计

方程（1）为非线性微分方程组，很难求出其解析解，本文采用数值方法进行参数估算.对于S（t），I1（t），I2（t），R（t）的一组测量数据S=｛S（ti）｝，I1=｛ I1（ti）｝，I2=｛ I2（ti）｝，R=｛ R（ ti）｝（i =1，2，…，n），令则参数估计问题转化为无约束非线性优化问题，求得f的最小值minf即为目标函数.其中：S，I1，I2， R为观测值；为相应的估计值；表示泛函中的2-范数的平方.为得到函数（3）的具体表达式，利用数值积分公式可得

其中：A，B，C，D分别为式（4）～（7）所表示的估计值.

将数据代入式（8）中即可得到关于8个参数的多项式，记为f（a，b，d，d，As，ε，β（N），γ），为求得f（ a，b，d，d， As，ε，β（N），γ）的最小值，将它分别对8个参数进行求导，可得8个非线性方程所组成的非线性方程组，记为

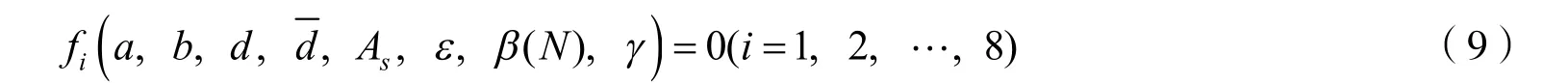
采用牛顿法求解非线性方程组（9）.牛顿法求解非线性方程组就是将非线性问题线性化，为减少计算次数和得到较为精确的结果，选取合理初值就显得尤为重要，这里采用最速下降法选取合理初值，记为

4　数值实验与结果分析

以2004—2013年江苏省相关麻风病数据（数据来源于公共卫生科学数据中心，相关网站为http：//www.phsciencedata.cn/）为例，对本文所建模型的未知参数进行估计，时间区间为［0，9］，采样步长为Δt = 1 .利用软件得到的参数计算结果为a=0.31，b =0.87，d =0.08，ε=0.23，γ=0.93，β（N）=0.65，As=0.26，d =0.05.为验证本文方法的有效性与精确性，将参数估计值代入模型（1）中，采用Runge-Kutta法求得其数值并进行数据仿真，得到I1（t），I2（t），R（t）的拟合曲线（见图1）.由图1可以看出，该方法所得计算结果与实际观测数据吻合程度相对较高.

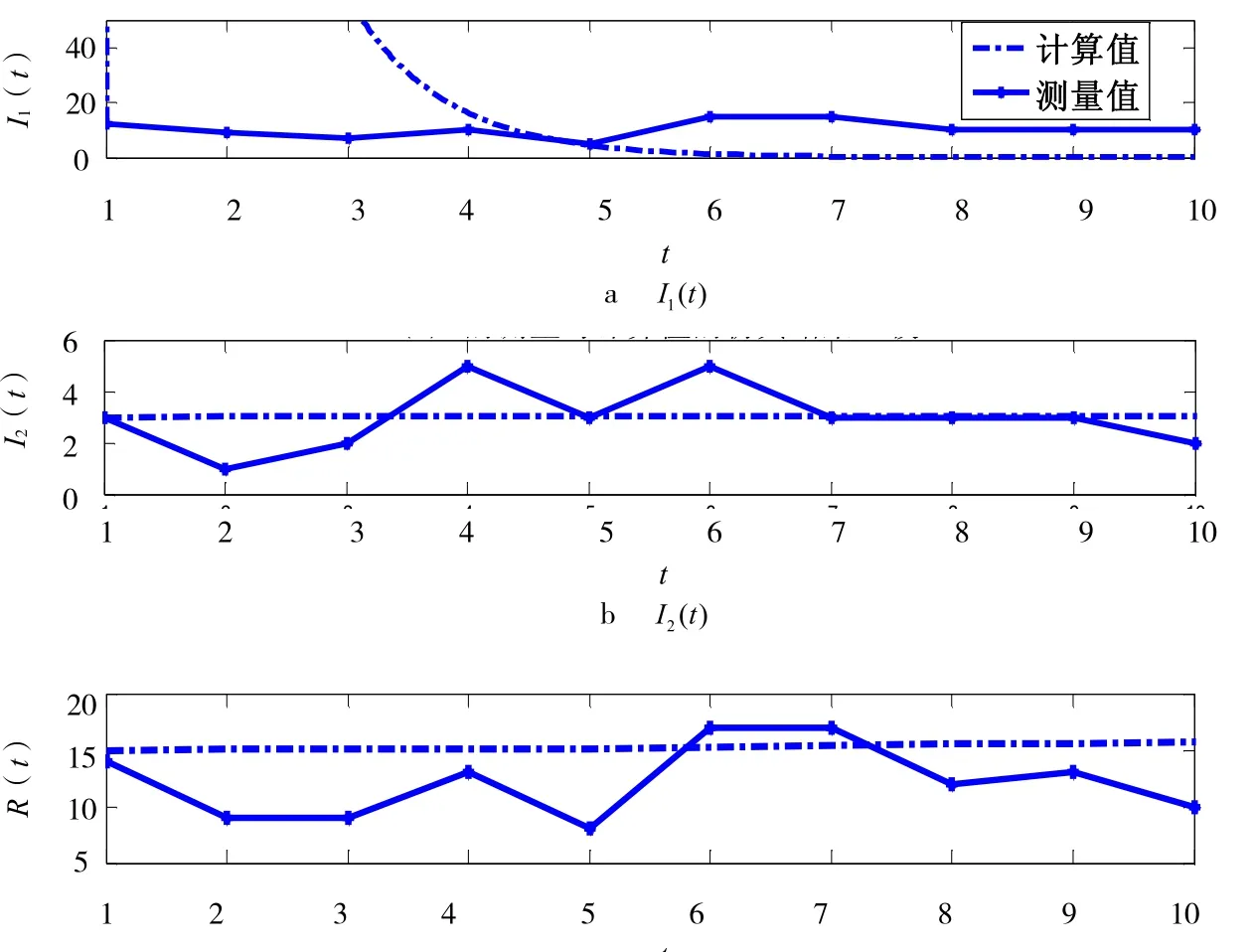
图1 I1（t），I2（t），R（t）仿真结果

由于查找的数据十分有限且时间跨度较大，部分缺失值的填充参入过多主观因素，使得数据拟合效果与预想有一定的偏差，对本文计算方法的精确性的验证产生了影响，但并不能否认该方法的正确性与实用性.若有相对较为精确的数据，本文计算方法将会得到较好的验证.

5　结论

对于SIRS传染病模型的参数估计问题，本文运用了基于数值算法的参数估计，首先结合三次Hermite插值多项式得到一个高精度的数值积分公式，利用该公式对传染病模型进行离散化，进而将参数估计问题转化为无约束优化问题，将数据代入后得到关于各个参数的多项式.为求得该式的最小值，将其分别对各个参数进行求导，进而得到关于各个参数的非线性方程组，利用最速下降法取得参数的合理初始值，最后利用牛顿法求得各个参数值.并针对江苏省患麻风病情况进行了仿真对比，仿真结果表明，该算法所得结果与实际数据统计结果具有较好的拟合度.因此，本文的参数估计算法在估计类似传染病模型参数上是可行和可信的.

参考文献：

［1］ 刘利斌，刘翠萍，张永，等.基于粒子群算法的捕食者-食饵模型的参数估计［J］.纯粹数学与应用数学，2016，32（1）：19-25

［2］ 孙有发，郭旭冲.现实复杂情形下的SIRS型传染病模型及其控制策略［J］.系统仿真学报，2010，22（1）：195-200

［3］ 张海峰，傅新楚.含有免疫作用的SIR传染病模型在复杂网络上的动力学行为［J］.上海大学学报：自然科学版，2007，13（2）：189-192

［4］ 燕振刚，胡贺年，李广.基于粒子群算法的Richards模型参数估计和算法有效性［J］.计算机应用，2014，34（10）：2827-2830

［5］ 曹怀火，李海燕，伏升茂.基于混合加速粒子群算法的捕食者-食饵模型参数估计［J］.生物数学学报，2013，28（3）：553-557

［6］ 马新生，王来群，胡文玉.基于潜周期模型的两种群食饵-捕食者模型的参数估计［J］.南昌大学学报，2008，30（2）：134-137

［7］ 柳寅，马良，黄钰.基于模糊粒子群算法的非线性函数优化［J］.上海理工大学学报，2012，34（4）：314-317

［8］ 李斌，李文峰.基于仿真的优化的粒子群算法参数选取研究［J］.计算机工程与应用，2011，47（33）：23-24

Parameter estimation of the SIRS infectious disease model based on numerical integration

SONG Dan-dan，WANG Jing-nan，YANG Guang-xu，LI Jia-si，YANG Jia-xin
（School of Applied Science，Harbin University of Science and Technology，Harbin 150080，China）

Abstract：The third-order Hermite interpolation function and numerical integral formula are applied to an SIRS infectious disease model.Based on the principle of minimum error， the parameter estimation problem in the model is transformed to the unconstrained optimization problem and a polynomial can be obtained after the data is substituted into the formula.In order to get the minimum value of the polynomial， the partial derivatives of the polynomial with respect to each parameter are obtained after which a system of nonlinear equations related to the model is obtained. The steepest descent method is used to get a set of accurate and reasonable initial values，based on which Newton method is used to solve the nonlinear equations and then the specific parameter values are obtained.Finally，the equilibriums of SIRS model and the effectiveness of general parameter estimation are validated by numerical simulations.

Key words：SIRS model；numerical integration；Newton method；numerical simulations；parameter estimation

中图分类号：O29

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.004

文章编号：1007-9831（2016）05-0010-05

收稿日期：2016-04-15

基金项目：哈尔滨理工大学大学生创新项目（201512）；哈尔滨理工大学教学改革项目（320150023）

作者简介：宋丹丹（1991-），女，黑龙江齐齐哈尔人，在读本科生.

通信作者；王晶囡（1978-），女，山东平度人，副教授，博士，从事微分方程研究.E-mail：wangjingnan@hrbust.edu.cn