基于图论算法的微博好友圈及消息发布方案研究

李冬梅，简国明，王尚九，李少勇，杜磊，周碧江

（韶关学院 数学与统计学院，广东 韶关 512005）



基于图论算法的微博好友圈及消息发布方案研究

李冬梅，简国明，王尚九，李少勇，杜磊，周碧江

（韶关学院 数学与统计学院，广东 韶关 512005）

摘要：以微博用户为顶点，建立用户关注关系的顶点赋权有向图模型，把寻找微博中的最大好友圈问题转化为有向图的最大有向完全子图问题，而选择发布某消息的用户数最少的方案问题转化为寻找有向图的最小支配集问题.采取用户间关注关系0-1矩阵及好友关系的无向图，应用启发式着色算法求解无向图中的最大完全子图，计算出最大好友圈.根据消息传播关联的0-1矩阵，应用有向图的最小支配集的优化算法，求解最小支配集，得出了发布某消息的用户数最少的方案.

关键词：微博；图论算法；好友圈；最大完全子图；最小支配集

微博，作为一种新兴的交流工具，以简单快捷的操作方式和随时随地发布信息的互动形式，在各类网络社交服务中独树一帜［1-2］.在微博中，相互关注的用户被称为好友，对于一个群体，如果他们相互之间均为好友，则称为好友圈.文献［3］讨论了微博用户、微博消息的各影响因子及影响力问题，并给出了相关计算结果.本文采用南京师范大学2014年数学建模竞赛题相关数据（其中，数据文件data1.xls包含了这些用户的相互关注数据，每一行为该行号对应的用户对其它用户的关注信息；数据文件data2.xls为若干消息数据，每一行为用户发布或转发的消息编号），并假设一微博用户发布的消息，其粉丝都会看到（不考虑转发），考虑某微博有N个（如N =10 000）用户群体，已知每个用户关注其它用户的关注数据，同时已知每个用户发布或转发的具体消息数据，消息总数为M个（如M =500），运用图论算法，计算出最大好友圈人数最多的好友圈，得出了发布某消息的用户数最少的方案.

1　微博好友及消息问题的图论表示

本文假设：各个用户间在短时间内没有关注新的用户和取消对其他用户的关注；用户在发布或者转发微博消息后在短时间内不会再去删除此消息；用户间不存在僵尸粉现象.

对于有N个用户的微博群体，以每个微博用户作为顶点，若微博用户A关注微博用户B，则A到B连一条有向边，得到一个有向图D（V，E），其中：V是顶点集；E是有向边集.有向图D（V，E）是微博用户群体的关注（关系）有向图.顶点A的出度d+（ A）是对应用户A的关注数，而顶点B的入度d-（ B）是对应用户B的被关注数［4-5］.每个微博用户发布或转发消息数视为顶点的权，得到顶点赋权有向图D（V，E）（见图1）.在D（V，E）中考虑两顶点相互连边（即好友）的群体，称为好友圈，好友圈就是一个有向完全图，寻找人数最多的好友圈实质上就是寻找有向图D（V，E）的极大有向完全图中的最大有向完全子图；而选择发布某消息的用户数最少的方案问题就是寻找有向图D（V，E）的最小支配集问题.

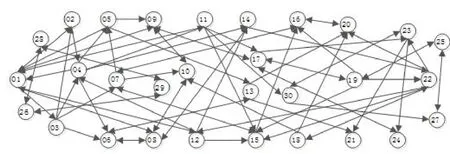
图1 有向图D（V，E）

2　微博最大好友圈的求解

2.1 关注关系的矩阵表示

在有向图D（V，E）中，考虑两顶点相互连边的子图，得到一个无向图，寻找人数最多的好友圈实质上就是寻找有向完全图中的最大有向完全子图.令aij表示用户i关注用户j情况，即当用户i关注用户j时，aij=1；当用户i没关注用户j时，aij=0（i，j=1，2，…，10000）.得到用户间关注关系的0-1矩阵A=（aij） .

2.2 启发式着色算法求解最大完全子图的基本步骤

启发式着色算法求解最大完全子图的基本步骤为：

Step1（构造出无向图G（V，E）） 由数据data1.xls，得到10 000个顶点的有向图D（V，E）及用户间关注关系的0-1矩阵A，通过Matlab软件编程，在10 000个顶点的有向图D（V，E）中寻找好友对，共找到3 935对好友，对每一对好友进行有向边连接，就形成了无向图G（V，E）.

Step2（精简预处理） 由于无向图的较大完全子图往往存在于度数较高的一定数量的顶点之间.因此，可以合理地删除掉无向图中较低度数顶点及边.

Step3（初始化） 记Fd表示未着色顶点的已着色邻接顶点个数，Ud表示未着色顶点的未着色邻接顶点个数.找出初始状态时每个顶点的Fd和Ud，并按照一定的顺序放置颜色c1，c2，…，ck；对于无向图G（V，E），初始状态时，每个顶点的Fd=0，每个顶点的Ud等于每个顶点的度数，并赋颜色初始值为0.

Step4（顶点着色） 对Fd最大的顶点V着色；若每个Fd相同，则对Ud最大的顶点V着色；若Fd，Ud都相同，则从编号较小的顶点开始着色.

着色的颜色ck选择原则：k为颜色的编号，若ck这种颜色已经出现过，则着ck这种颜色的顶点只能落在已着色顶点V的邻接顶点范围内.若在顶点V的邻接顶点范围内，出现某一邻接顶点不与已着ck这种颜色的其他邻接顶点相邻，则选择下一种颜色ck+1为该邻接顶点着色.

Step5 重复步骤4，直到顶点V的所有邻接顶点都着色为止.

Step6 回到Step3，找出每个未着色顶点的Fd和Ud，重复Step4、Step5，直到所有顶点都已着色为止.这样就实现了无向图G（V，E）划分为其极大完全子图的并集，即G（V，E）=G1（V1，E1）∪G2（V2，E2）∪…∪Gk（Vk，Ek）∪…，且Gi（Vi，Ei）∩Gj（Vj， Ej）=Ø（i≠j）；V（G）=V（G1）∪V（G2）∪…∪V（Gk）∪…，且V（Gi）∩V（Gj）=Ø（i≠j），Gi（Vi，Ei）=Gi（i=1，2，3，…）表示无向图G（V，E）的极大完全子图.

Step7 通过比较所有的极大完全子图，得到最大完全子图［6］.

2.3 启发式着色算法求解最大完全子图的求解结果

根据启发式着色算法求解最大完全子图的基本步骤，运用Matlab编程求解，得到由13个用户所构成的好友圈为最大好友圈，分别是用户867，2 529，2 886，3 077，3 206，3 222，3 646，4 012，4 831，5 630，6 241，7 408，8 857.而最大完全子图见图2.

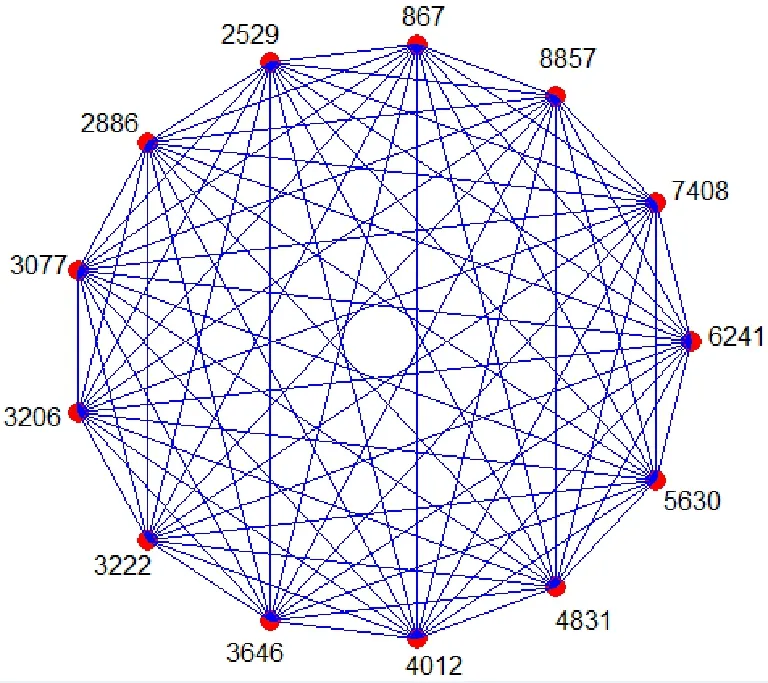
图2 最大完全子图

3　微博消息用户最少的发布方案求解

考虑消息传播关系的有向图D（V，E），这样求用户最少的发布方案问题就是求有向图的最小支配集问题［7］.令bij表示用户i是否看到用户j发布的信息，即当用户i能看到用户j发布的信息时，bij=1；当用户i不能看到用户j发布的信息时，bij=0（i，j=1，2，…，10000）.得到0-1关联关系矩阵B=（bij），顶点v的出度越大，表示顶点v能支配的顶点越多，顶点v成为最小支配集中的元素的可能性越大，而0-1关联矩阵中的每一列之和分别表示对应顶点的出度，每一行之和分别表示对应顶点的入度.

用户最少发布方案的算法步骤为［8］：

Step1 读取文件data2.xls的数据，通过Matlab软件编程，得到消息传播过程中用户之间的关联矩阵B .

Step2 找出粉丝数最多的用户.对Step1得出的0-1矩阵B的每一列进行求和，求和值记为sj（j=1，2，3，…，10 000），表示用户j发布消息能让sj个之前未看到此消息的用户看到此消息，再从sj（j =1，2， 3， …，10 000）中找出最大的一列，表示能让最多之前未看到此消息的用户看到该消息，并将sj最大的列对应的用户列入最小支配集作为消息的发布用户.

Step3 找出看过消息的用户.将sj最大的列中的1转化为0，表示sj最大的列对应的用户的粉丝已看过此消息，同时将sj最大的列对应的用户所对应的行中的1也转化为0，表示此用户已发布过此消息.至此，得到一个新的0-1矩阵B .

Step4 重复Step2和Step3，直到对矩阵B的任意一列和行求和都为0为止.

在确保所有用户都能看到（不考虑转发）的条件下，得到发布某消息的用户数最少的发布方案.该方案需要251个用户发布此消息，具体结果省略.

4　结束语

本文在建立确定最大好友圈模型时，将实际问题转化为图的最大完全子图，利用启发式着色算法求解最大完全子图，该算法思路清晰，提出了精简措施，不仅提高算法运行效率，而且适用于多顶点的无向图.

针对消息发布用户进行最优化，通过将问题转化为有向图的顶点支配问题，列出相关的0-1矩阵，基于有向图的最小支配集的优化算法寻找最优方案.本文在新闻传播、信息推荐、民意调查、电子商务、网络营销或网络代购等领域有一定的借鉴作用和应用价值.

参考文献：

［1］朱文俊，张宁，聂雨薇.基于图论的微博消息传播对微博影响力的研究［J］.广角，2015（17）：267-269

［2］原福永，冯静，符茜茜.微博用户的影响力指数模型［J］.情报分析与研究，2012（6）：60-64

［3］简国明，李冬梅，李少勇，等.微博用户及消息的影响力研究与建模［J］.佛山科学技术学院学报，2016，34（3）：1-5

［4］徐俊明.图论及其应用［M］.合肥：中国科学技术大学出版社，1998

［5］王桂平，王衍，任嘉辰.图论算法理论、实现及应用［M］.北京：北京大学出版社，2011

［6］李建新.求最大完全子图的启发式着色算法［J］.滁州学院学报，2010，12（2）：9-11

［7］董敏，汤建钢.求解最大完全子图的一种DNA算法［J］.江汉大学学报：自然科学版，2012，40（1）：20-23

［8］高文宇.有向图连通支配集求解算法［J］.计算机工程与应用，2010，46（21）：9-13

Research on micro-blogging friends circle and news release scheme based on graph theory algorithm

LI Dong-mei，JIAN Guo-ming，WANG Shang-jiu，LI Shao-yong，DU Lei，ZHOU Bi-jiang
（School of Mathematics and Statistics，Shaoguan University，Shaoguan 512005，China）

Abstract：With micro-blogging users as the vertex，the micro-blogging biggest problem is translated into the largest complete sub-graph problem of directed graph through building vertex weighted directed graph model between the relationship of user attention，and the number of users in a news release minimal solution problems is translated into looking for the smallest dominating set problem of directed graph.Taking attention to the 0-1 matrix of relationship between user attention and friendships of undirected graph，the maximum friends circle is calcutated by the heuristic coloring algorithm for undirected graph the maximum complete sub-graph.According to correlation 0-1 matrix of the message spread and the minimum dominating set of optimization algorithms of a directed graph，the minimum dominating set is solved，then the least number users of a news release program is obtained.

Key words：micro-blogging；graph theory algorithm；friends circle；largest complete sub-graph；minimum dominating set

中图分类号：O157.6

文献标识码：A

doi：10.3969/j.issn.1007-9831.2016.05.005

文章编号：1007-9831（2016）05-0015-04

收稿日期：2016-03-01

基金项目：2015年度广东大学生科技创新培育专项资金项目（团粤联发［2015］50号，pdjh2015b0477）；2014年广东省本科高校教学质量与教学改革工程项目（粤教高函［2014］97号）

作者简介：李冬梅（1992-），女，广东英德人，在读本科生.

通信作者：简国明（1958-），男，江西南昌人，教授，硕士，从事代数图论、数学模型和数学教育研究.E-mail：527775876@qq.com