浅谈初中数学“化归思想”之转化

江西省上饶市信州区秦峰中学 朱校华

使用2012人教版七（下册）教科书即进入七年级第二学期后，第十周周四与周五举行的期中（六中集团联考）数学卷第14题（3分填空题）中，提到了使用“方程思想”解决将循环小数转化成分数技能检测。原题是这样的：

无限循环小数可转化为分数，例如，将转化为分数时，可设则有解得即仿此方法，将化 为分数是___.

本题内含的自身解法按模仿套路并不难：

设则依据等式就有y= 0 .45 + 0.01y解之得：似乎找到了规律：

有一个循环节，转化成分数时，分母就是一个9，分子照抄；有两个循环节，转化成分数时，分母就是两个9，分子照抄……

不妨把上面这种循环小数叫做“纯循环小数”。

例如：负循环小数类似。

事实上，我们对于属于有理数的小数（主要指有限小数与无限循环小数）均可以转化成分数（对于无限不循环小数是不可以转化成分数的）。

（一）任何一个有限小数均可以转化成分数

例如，即转化规律为：看小数点后面有多少位，相应分母就带上多少个0，分子照抄。

（二）遇上一个混循环小数如何转化成分数呢

例如，转化成分数为_____.

转化的精华在于利用已知或者原有规律来解决新问题。换句话说，仍借助于纯循环小数来过渡，这才是转化的实质！

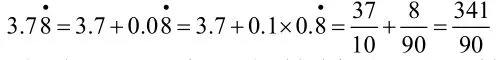
总结：混循环小数转化成分数的策略是现将非循环部分与循环部分分开，非循环部分套有限小数的转化方法走，循环部分朝着纯循环小数转化成分数的思路走，最终通分合并成一个分数（要求最终结果应该是最简分数）。

巩固练习：将转化成分数为_____.

课后思考：一个特殊分数如，反过来怎样写成循环小数的形式呢？

以上谈的是代数学上的转化，其特设处在于具有系统性、连贯性与对比性。下面通过看此次试卷上的第24题中的第（3）小题，在解决时又是怎样转化的呢？这是几何题可使用“分离法”即“分离基本图形法”的代表，众所周知：

解几何题有“三板斧”：①记已知 ②观 图形 ③想 未知。

解几何题有“二踢腿”：由“已知”想“可知”；拿“未知”找“需知”。

解几何题有“一中心”：以“基本图形”为中心，使用“分离法”寻关系。

正是有了上面的“三二一”手段，解决几何问题我们照样可以转化。

看原卷上的第24（3）题：

如图201605041示，过点C作CD垂直Y轴于点D，点P为线段CD延长线上一动点，连接OP，OP平分∠AOP，OF垂直OE.当点P运动时，的值是否会改变？若不变，求其值；若改变，说明理由。

首先，本题图含有

第一基本图形：互为邻补角。

在一组互为邻补角图中，增加了“角平分线”想到：一组邻补角的平分线互相垂直。可知图中有“若OE平分∠AOP，OF平分∠POB”即得出“OE垂直OF”.变换一种方式可以为：“若OE平分∠AOP，OE垂直OF”同样可以得出“OF平分∠POB”。于是∠POF=2∠FOB.显然这里头隐含着∠AOE+∠FOB=90°这个结论。

第二基本图形：平行线中的三线八角。

由C P平行于X轴，得到∠OPD=∠POB=2∠FOB.

结合∠DOE+∠AOE=90°是天然的直角，利用“同角的余角相等”立马得到∠DOE=∠FOB.故∠DPO=2∠DOE.说明的值等于2.问题得以解决。