浅析如何让学生把握数学概念
新疆兵团第四师六十六团一中 王再玲
数学概念是人类对现实世界空间形式和数量关系的概括反映,是建立数学法则、公式、定理的基础,也是运算、推理、判断和证明的基石,更是数学思维、交流的工具,包括了概念的名称(符号)、定义、属性、例子。例如,“单项式”的概念,“单项式”是概念的名称,“由数或字母的积表示的式子叫做单项式,单独的一个数或一个字母也是单项式”是概念的定义,积的形式是概念的属性,例子:2a,ab,b2,5,a等。在初中阶段要学习的数学概念非常多,很多时候提问学生一个数学概念,定义,性质,判定时,学生不是回答不完整,就是随意改动概念中的一些关健字句,这样对概念模糊的认识导致学生在解题中的困难。而且长期以来数学教师在备课时已经把教材内容进行了提炼,在课堂上通过自己的语言表达给学生,而大部分学生是被动的接受和理解,学生没有进行课前预习,事实上长期以来很多学生基本不用数学教科书,只有在做作业时才拿出来抄题目,所以对数学概念的理解印象不深,时间一长容易忘记,那么在初中数学教学中,如何让学生能牢记数学概念并能把握数学概念的实质?
一、注重概念的本源,引入概念
每一个概念的产生都有丰富的知识背景,舍弃这些背景,直接抛给学生一连串的概念是传统教学模式中司空见惯的做法,这种做法常常使学生感到茫然,丢掉了培养学生概括能力的极好机会。自然界对一切想像的数量都提供了原型。利用这些具体的原型引入概念是一种最基本、最常用的方法。
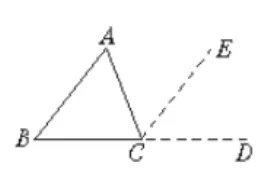
数学概念的建立是解决数学问题的前提,学生在运用数学概念进行推理、判断过程中要得出正确的结论,首先要正确地掌握概念、理解概念。“学习最好的途径是自己去发现”。在学习三角形内角和概念时,教科书中直接给出了小学利用“剪拼”方法发现了三个内角恰好拼成一个平角,得到了结论“三角形的内角和是1800”同时从这种“剪拼”过渡到(如图所示):“证明三角形的内角和是1800”,引导学生认识到这种“动手操作”是添加辅助线的方法,也是发现教学结论,得到数学概念的常用手段之一。学生如能在教师创设的情景中去“想数学”“经历”一遍发现、创新的过程,那么在获得概念的同时还能培养他们的创造精神。由于概念教学在整个数学教学中起着举足轻重的作用,我们应重视在数学概念教学中培养学生的创造性思维。
引入是概念教学的第一步,也是形成概念的基础。概念引入时教师要鼓励学生猜想,如学生在学了平行四边形的性质定理和判定定理以后,在学习矩形和菱形的性质定理和判定定理时,可以让学生从“边、角、对角线”三个方面去猜测一下它们的性质定理和判定定理,即让学生依据已有的材料和知识作出符合一定经验与事实的推测性想象,让学生经历发现新概念的最初阶段。在概念引入时培养学生敢于猜想的习惯,是形成数学直觉,发展数学思维,获得数学发现的基本素质,也是培养创造性思维的重要因素。
二、立足教材,图文结合
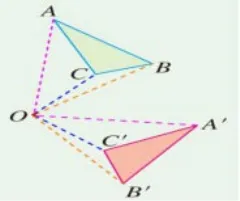
数学概念语言抽象,内涵丰富,数学语言具有简洁、无歧义的特点,必须认读感知阅读材料中有关的数学符号、图形符号等,理解每个数学术语。而这些符号往往内涵丰富,与自然语言差别很大,所以学生在理解上就有了一定的困难,采用图文结合的形式可以帮助学生很好的理解概念,如当学生已初步了解“旋转角”的概念,为了让学生能牢固掌握概念,出示如图所示的旋转图形,边指着图形从点A和点A,,划到O点,边口述旋转角的概念“对应点到旋转中心所连线段的夹角等于旋转角”,然后再换一对对应点,点B和点B,,在图上比划的同时让学生叙述哪一个等于旋转角,再换到别一对对应点C和C,,用同样的方法再让学生正确叙述一次概念的内容。数学中很多的概念都可利用图形来牢记,这里绝不是简单地要求学生死记硬背,而是让学生在复述过程中把握概念的重点、要点、本质特征。
三、加强概念的应用训练
概念一旦获得,如不及时巩固,就会被遗忘。概念的获得是由特殊到一般,概念的运用则是从一般到特殊。学生掌握概念不是静止的,而是主动在头脑中进行积极思维的过程,它不仅能使已有知识再一次形象化和具体化,而且能使学生对概念的理解更全面、更深刻,同时还能提高学生的实践应用能力。如学习了有理数的加法法则后,出示一组计算题,-3+(-5)=,3+(—5)=,教师板书计算过程,解:-3+(-5)=-(3+5)=-8,学生叙述“同号两数相加,取相同的符号,并把绝对值相加”,板书3+(-5)=-(5-3)=-2时,学生叙述“绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值”,教师的板书过程和学生的叙述相呼应,学生在这样的训练过程中明确数学概念是我们解题的理论依据,在接下来的有理数的混合运算中都是运用同样的方式来解答,让学生体会到我们计算的每一步都由相应的运算法则决定的。
数学教学离不开解题,在教学过程中引导学生正确灵活地运用数学概念解题,是培养学生解题技能的一个有效途径,如通过基本概念的正用、反用、变用等,培养学生计算、变形等基本技能。比如这样一个问题:“若a和b互为相反数,c和d互为倒数,x的绝对值是1,求(2a+2b)+(cd+a+b)x+x2的值”显然要解答此题,必须知道概念“互为相反数的两个数相加得0”的正用,“乘积为1的两个数互为倒数”的反用,和绝对值的概念,同时还要会进行适当的变形,把(2a+2b)变成2(a+b)的形式。因此,教师应该多给学生提供练习的机会,提高学生灵活应用概念的能力。
总之搞好数学概念的教学,使学生透彻地牢固地掌握数学概念是提高数学教学质量的关键所在,培养学生运用数学知识解决实际问题的能力,以及发展学生逻辑思维和空间想象能力的关系,在思想上重视它,这样使我们在教学时会目的明确,方法对头,既不会造成为概念而教学,也不会在数学教学时顾此失彼。

