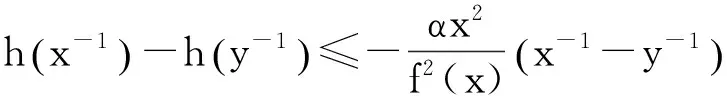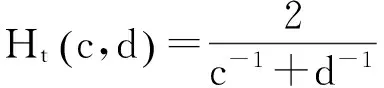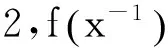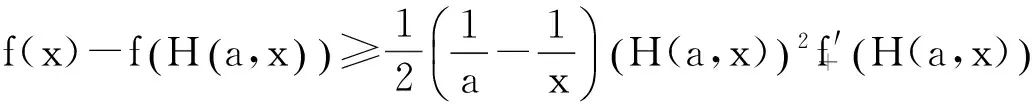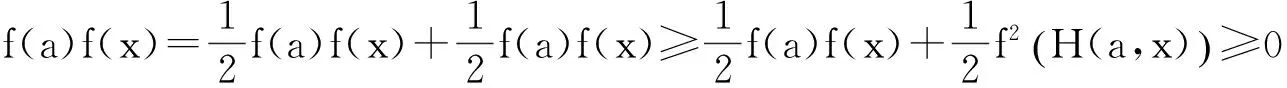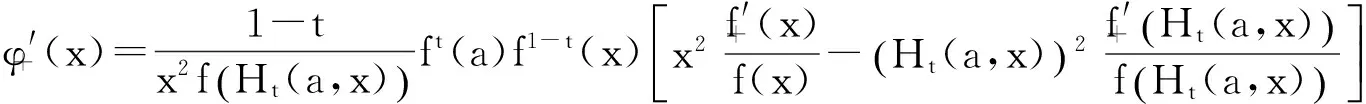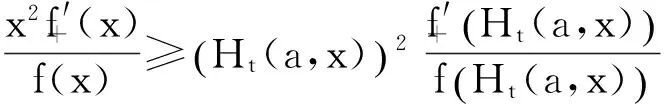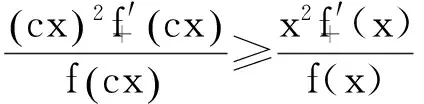与HG凸函数有关的若干单调函数

时统业，　秦　华，　王　斌

(1.海军指挥学院信息系，南京211800；　2.海军蚌埠士官学校航海系，安徽蚌埠233012)



与HG凸函数有关的若干单调函数

时统业1，秦华1，王斌2

(1.海军指挥学院信息系，南京211800；2.海军蚌埠士官学校航海系，安徽蚌埠233012)

[摘要]首先证明HG凸函数存在单侧导数.利用HG凸函数的定义和不等式，构造了若干函数，通过研究它们的单侧导数证明它们的单调性.

[关键词]HG凸函数； 对数凸函数； 单调性； 单侧导数

受文[1-5]的启发，本文给出一些与HG凸函数有关的单调函数.

定义1[6]设f(x)区间I上有定义，f(x)在I上称为是凸函数，当且仅当对任意x1，x2∈I，λ∈(0，1)，有

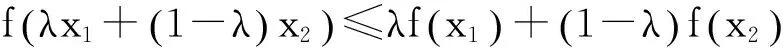
定义2[7]设f(x)是定义在区间I上的正值函数，如果lnf(x)为I上的凸(凹)函数，则称f(x)在区间I上是对数凸函数.

定义3[8]设区间I⊆(0，+∞)，f∶I→(0，+∞)，若对任意x1，x2∈I，t∈(0，1)，有

(1)

则称f是区间I上的HG凸函数.如果式(1)中的不等号反向，则称f是区间I上的HG凹函数.

引理1[8]设f∶[a，b]⊆(0，+∞)→(0，+∞)在[a，b]上二阶可导，则f是[a，b]上的HG凸(凹)函数的充要条件是：对任意x∈[a，b]有

引理3[5]设f∶I⊆R→(0，+∞)，则f是I上的对数凸(凹)函数当且仅当lnf∶x∈I→lnf(x)为I上的凸(凹)函数，故此时f在每一处都存在单侧导数，且f′+(x)≥(≤)f′-(x).

引理4[9]设f(x)为区间I上的凸函数，则f(x)在开区间(a，b)⊆I内处处存在左、右导数(从而处处连续)，且对x，y∈(a，b)，x

引理5[9]f(x)在区间(a，b)上为凸函数的充要条件是对任意x0∈(a，b)和α∈[f′-(x0)，f′+(x0)]，当x∈(a，b)时，有

引理6设f∶[a，b]⊆(0，+∞)→(0，+∞)是HG凸函数，则

(i)f在(a，b)各点处的单侧导数存在，且对任意x，y∈(a，b)，x

(2)

由此得

也即式(2)成立.

引理7[10]设f(x)是[a，b]上的连续函数，若f′+(x)或f′-(x)对一切x∈(a，b)有一个单侧导数存在，且非负(允许+∞)，则f(x)单调递增.

定理1设f∶[a，b]⊆(0，+∞)→(0，+∞)是二阶可微的HG凸函数，且2f(x)+xf′(x)在[a，b]上恒号，则函数

在[a，b]上单调增加.

证对任意x∈(a，b)，

因为f是HG凸函数，由引理1有

从而对任意x∈(a，b)，有f′1(x)≥0，即f1(x)在[a，b]上单调增加.

推论1.1设条件同定理1，则有

(3)

证由定理1知f1(x)在[a，b]上单调增加，所以有f1(b)≥f1(a)，由此证得式(3)成立.

推论1.2设f∶[a，b]⊆(0，+∞)→(0，+∞)是二阶可微的HG凸函数，且2f(x)+xf′(x)在[a，b]上恒正(负)，则函数

是[a，b]上的HG凸(凹)函数.

证由定理1有f1(x)≥f1(a)，于是有

由引理1知f2(x)是[a，b]上的HG凸(凹)函数.

定理2设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续的HG凸函数，则函数

在[a，b]上单调增加.

证对任意x∈(a，b)，

于是对任意的x∈(a，b)有R′+(x)≥0，由引理7知R(x)在[a，b]上单调增加.

定理3设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续的单调增加的HG凸函数，则函数

在[a，b]上单调增加.

证对任意x∈(a，b)，

由HG凸函数的定义有

又因为x≥H(a，x)，由引理6有

因此对任意x∈(a，b)有P′+(x)≥0，由引理7知P(x)在[a，b]上单调增加.

定理4设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续且单调的HG凸函数，则函数

在[a，b]上单调增加.

证显然θ(x)在[a，b]上连续.对任意x∈(a，b)，

由引理6有

故对任意x∈(a，b)有θ′+(x)≥0，由引理7知θ(x)在[a，b]上单调增加.

推论4.1设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续且单调的HG凸函数，则

(4)

证由定理2和定理4分别得到式(4)的左边和右边不等式.

定理5设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续的HG凸函数，t∈(0,1)，则函数

在[a，b]上单调增加.

证对任意x∈(a，b)，

因此对任意x∈(a，b)有φ′+(x)≥0，由引理7知φ(x)在[a，b]上单调增加.

定理6设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续的单调增加的HG凸函数，t∈(0，1)，则函数

在[a，b]上单调增加.

证对任意x∈(a，b)，

因此对任意x∈(a，b)有ψ′+(x)≥0，由引理7知ψ(x)在[a，b]上单调增加.

定理7设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续的单调增加的HG凸函数，t∈(0，1)，则函数

在[a，b]上单调增加.

证对任意x∈(a，b)，

以下证明类似于定理6的证明，这里略去.

定理8设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续的HG凸函数，则函数

在[a，b]上单调增加.

证对任意x∈(a，b)，

由引理6对任意x∈(a，b)有T′+(x)≥0，由引理7知T(x)在[a，b]上单调增加.

推论8.1设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续的HG凸函数，则

(5)

证由定理8知T(x)在[a，b]上单调增加，所以有T(b)≥T(a)，由此证得式(5)成立.

定理9设f∶[a，b]⊆(0，+∞)→(0，+∞)是连续的HG凸函数，常数c>1，则函数

在[a，b]上单调增加.

证对任意x∈(a，b)，

当c>1时，cx>x，由引理6有

因此对任意x∈(a，b)有l′+(x)≥0，由引理7知l(x)在[a，b]上单调增加.

[参考文献]

[1]胡克.解析不等式的若干问题[M].武汉：武汉大学出版社，2003：129-130.

[2]张小明，郑宁国.与几何凸函数有关的一些单调函数的构造[J].成都大学学报(自然科学版)，2005，24(2)：90-93.

[3]郑宁国.一些与几何凸函数有关的函数的准线性[J].高等数学研究，2008，11(4)：20-23.

[4]华云.与GA凸函数相关的函数的准线性[J].大学数学，2009，25(6)：193-196.

[5]张小明，褚玉明.解析不等式新论[M].哈尔滨：哈尔滨工业大学出版社，2009：180.

[6]裴礼文.数学分析中的典型问题与方法[M].2版.北京：高等教育出版社，2006：268.

[7]沈永欢，齐玉霞，张鸿林.简明数学词典[M].北京：新时代出版社，1989：258-259.

[8]陈少元，宋振云.HG-凸函数及其Jensen型不等式[J].数学的实践与认识，2013，43(2)：257-264.

[9]刘三阳，李广民.数学分析十讲[M].北京：科学出版社，2011.

[10]杨军.用单侧导数判断函数的单调性[J].四川师范学院学报(自然科学版)，2000，21(1)：108-109.

Some Monotone Functions Related to HG-Convex Functions

SHITong-ye1，QINHua1，WANGBin2

(1.Department of Information，PLA Naval Command College，Nanjing 211800,China；2.Department of Navigation，PLA Bengbu Naval Petty Officer Academy，Bengbu Anhui 233012,China)

Abstract:The existence of unilateral derivatives of HG-convex functions is proved.some monotone functions are constructed by means of the definition and inequalities for HG-convex functions，and their monotonicity are proved with unilateral derivative.

Key words:HG-convex function; logarithmic convex function; monotonicity; unilateral derivative

[收稿日期]2015-06-30

[作者简介]时统业(1963-)，男，硕士，副教授，从事基础数学教学与研究.Email：shtycity@sina.com

[中图分类号]O178

[文献标识码]C

[文章编号]1672-1454(2016)02-0073-05