求角度，强攻不取请绕行

李林明

如果将“求角度”看作一座城池，要想把它攻打下来，有时正面强攻未必是最好的办法 ，不如调整策略，绕到背后发动攻击，也许会达到事半功位的效果。

例1.在没带量角器的情况下，能否借助其他工具画出15°角？

在角的度量里，量角器确实是名符其实的“主力”，如果缺少它的“参与”，这“戏”好像还真无法演下去。

我们能否利用手中的一对三角板化解难题呢？我们知道，一副三角板的两组度数分别为：30°、60°、90°； 45°、45°、90°。

我们可尝试着进行多种“组合”得到15°角：

方案1：45°-30°=15°；

方案2：60°- 45°= 15°；

方案3：90°-30°-45°=15°

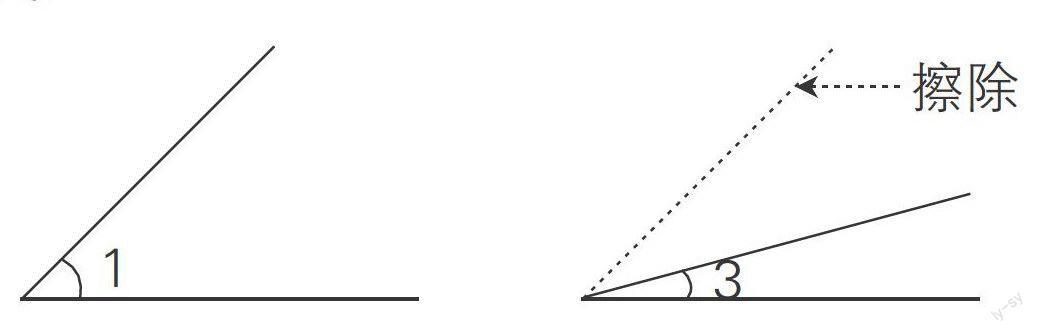
通过比较，方案1、2简捷、明了，应为首选方案。以方案1为例，可先画出一个45°的角（如左下图）。接着，在∠1的内部画出一个30°的角。最后，擦除多余的边，所余下的∠3就是所要画的角（如右下图）。

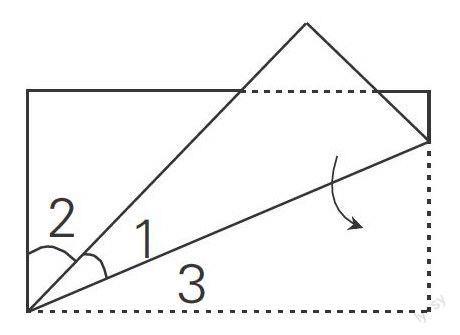
例2.把一张长方形的纸折成如下图所示的形状，若己知∠1的度数为23°，∠2的度数是多少？

如果仅从已知条件直接破解，会发现条件不足。这时，我们可以想：既然是“折纸”，里面就一定会隐藏着秘而不宣的条件——如直角或平角。假若我们沿着折痕将角“放回”（如右图）。会发现原来∠1与∠3是同一个角，它们与∠2共同构成了一个直角。于是：∠2=90°-23°-23°=44°。

怎么样，通过这些例子的讲解你对如何求出角的度数应该有新的认识了吧？我猜，你一准会说出——角的度量并不难，强攻不取就绕行吧！哈哈，对了，事实就是如此！