高职高专“高频电子线路”振幅调制的教学方法探析

黄文锋

(厦门海洋职业技术学院，福建厦门 361100)

高职高专“高频电子线路”振幅调制的教学方法探析

黄文锋

(厦门海洋职业技术学院，福建厦门 361100)

“高频电子线路”是电子信息类专业的一门重要课程，振幅调制是该课程的重要章节。该部分内容难度大、要求高。为了深入浅出地进行教学，在总结常规教学方法的基础上，提出从概念入手，先给出波形图、再求表达式的创新教学方式，更适合对数学要求不高的高职高专学生学习。

振幅调制；创新教学；高职高专

引言

“高频电子线路”在电子信息类专业中，具有非常重要的地位，它是电子工程、通信工程等电子信息类专业重要的专业基础课程。[1]调制是“高频电子线路”课程的重要章节，该章节的常规教学方法对原理阐述过于机械，对数学基础要求高，难以将概念、波形图、表达式融会贯通，高职高专学生不容易接受。针对高职高专该部分内容的教学，本文以振幅调制为例，提出创新教学方法，即从振幅调制的概念入手，先给出波形图，再求出调幅波的表达式，更容易让高职高专学生接受。

1 常规教学方法

以普通调幅为例进行阐述。各类教材对于普通调幅的电路组成模型一般有两种，如下图2-1，图2-2。两种方式原理类似，都是通过乘法器实现普通调幅方式，因此下面仅以图2-1作简单阐述。

调幅波uAM(t)=uo(t)=Am[UQ+uΩ(t)]*uc(t)= Am[UQ+uΩ(t)]Ucmcos(ωct)

=[AmUQUcm+AmUcmuΩ(t)]cos(ωct)

=[Umo+kauΩ(t)] cos(ωct)

其中Umo= AmUQUcm为载波电压振幅，ka=AmUcm为比例常数。

将uΩ(t)= UΩmcos(Ωt)代入以上表达式：

uAM(t)=uo(t)=[Umo+kaUΩmcos(Ωt)]cos(ωct)

= Umo[1+macos(Ωt)]cos(ωct)

其中ma=kaUΩm/ Umo为调幅系数。

2 创新教学方法

以上教学方法从纯数学的角度推理出调幅信号的表达式，较枯燥且不容易理解掌握。首先在乘法器的使用上，学生可能无法理解为什么要用乘法器来实现调幅波，没有很好的解释两者之间的关系。其次，整个调幅波的推导过程是纯数学推导，涉及到相量、三角函数等较多知识，对高职高专生来说可能难度较大。最后，调幅波的公式与概念以及波形图联系不大，没有很好地将整个知识体系融会贯通。基于以上种种因素，本人考虑从振幅调制的概念入手，通过先给出波形图，再求调幅波表达式的创新教学方式，可以很好地解决以上问题。

振幅调制：用调制信号去控制高频载波的振幅，使高频载波的振幅按照调制信号的规律变化。振幅变化的轨迹称作调幅信号的包络线，调制后的载波称调幅波。[2]

根据以上概念，可以得出结论：调幅波的振幅是在高频载波的幅值基础上再叠加与调制信号成比例的幅值；调幅波的频率与高频载波相等。因此可以先给出调制信号、高频载波和调幅波的波形如下：

调制信号uΩ(t)：

高频载波uc(t)：

调幅波uAM(t)：

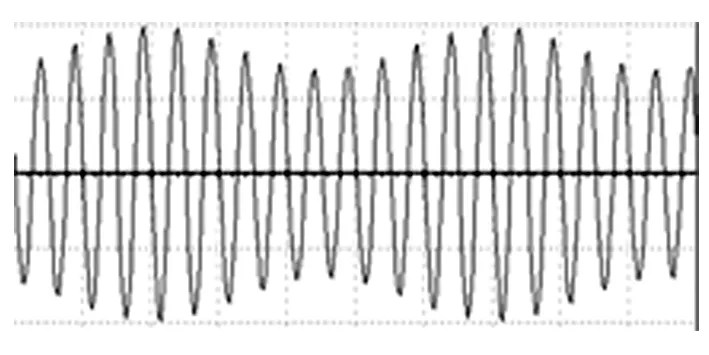
上图中，调幅波的振幅是在高频载波的幅值基础上再叠加与调制信号成比例的幅值，调幅波的频率与高频载波相等，图形与定义相符。[3]先给出概念和波形，让学生首先对振幅调制知识点有一个框架，更容易对振幅调制进行理解和掌握。以图形的形式将概念呈现给学生，也更适合数学基础较薄弱的高职高专生接受。

根据以上调幅波的图形及振幅调制的概念，可以通过正弦波的表达式：【幅值cos(角频率*t)】来写出调幅波的表达式，其中幅值是在高频载波的幅值基础上再叠加与调制信号成比例的幅值，角频率与高频载波相等。具体如下：

调幅波幅值= Ucm+kauΩ(t)，其中Ucm为高频载波幅值，ka为比例常数。

调幅波角频率=ωc。

代入表达式：调幅波=【幅值cos(角频率*t)】，如下：

调幅波uAM(t)=[Ucm+kauΩ(t)]cos(ωct)

将uΩ(t)= UΩmcos(Ωt)代入以上表达式：

uAM(t) =[Ucm+kaUΩmcos(Ωt)]cos(ωct)

= Ucm[1+macos(Ωt)]cos(ωct)

ma=kaUΩm/ Ucm为调幅系数。

由此可以发现，该方法所得出的表达式与通过乘法器相乘的数学推导结论一致，说明了它的正确性。该方法从振幅调制的概念入手，通过对定义的理解以及对波形的理解，可以轻而易举地写出调幅波的表达式，对于高职高专生来讲更容易掌握，也更与该课程的课程目的相符合。因此，在针对高职高专学生的授课过程中，可以采用该方法进行讲解，达到事半功倍的效果。

另外，针对调制的另一个重要内容：频率调制，同样可以参考该模式，主要区别在于由幅值变化转换成角频率的变化。以下对调频波作简单介绍。

调频(FM)：用调制信号去控制高频载波的频率，使高频载波的频率按照调制信号的规律变化。[4]即调频波的频率(角频率)是在高频载波的频率(角频率)基础上再叠加与调制信号成比例的频率(角频率)，调频波的幅值与高频载波相等，[5]具体表达式如下：

调频波角频率=ωc+kfuΩ(t)，其中ωc为高频载波角频率，kf为比例常数。

调频波幅值= Ucm。

注意此时角频率是变量，不能再简单参照振幅调制表达式【幅值cos(角频率*t)】，而应对角频率求积分，即【幅值cos(∫角频率dt)】，可以得出调频波的表达式为：

uFM(t) =Ucmcos∫[ωc+kfuΩ(t)]dt= Ucmcos(ωct+mfsinΩt)，mf为调频指数。由于调频波不是本文的重点，高职高专生也不必过分追求数学推导过程，因此对详细推导过程不再赘述。

结语

本文研究“高频电子线路”课程关于振幅调制章节的教学方法。首先总结传统的教学方法，即采用乘法器，将调制信号与高频载波相乘，通过数学推导的方式，得出调幅波表达式。该教学方法从纯数学的角度推理出调幅信号的表达式，较枯燥且不容易理解掌握。接着提出创新教学方法，从振幅调制的概念入手，先给出波形图，再求调幅波表达式。该方式对于高职生来讲更容易掌握，也更与该课程的课程标准、目的相符合。最后简单介绍了调频波的教学方式。希望本文能给高职高专高频电子线路课程教师提供参考借鉴。

[1]万云.高频电子线路实验教学改革探讨[J].科教导刊(电子版)，2014, (6): 48-48.

[2]王春生.浅析电视信号传输技术[J].软件，2012, 33(7): 101-102.

[3]李力厚，张居卫.浅谈调制技术分类和工作原理[J].河南科技(上半月)，2014, (8): 2-3.

[4]周胜源，陈高润，陈名松.System View在《高频电子电路》课程教学中的应用[J].桂林电子工业学院学报， 2004, 24(4): 106-109.

[5]门宏.调频信号的发射与接收[J].无线电，2009, (4): 90-92.

[6]胡宴如.高频电子线路[M]. 北京：高等教育出版社，2008. 94-95.

[7]申功迈，钮文良.高频电子线路[M].西安：西安电子科技大学出版社，2008. 99-100.

Research on the Teaching Method of “High Frequency Electronic Circuit” Amplitude Modulation in Higher Vocational Colleges

HUANG Wen-feng

(Xiamen Ocean Vocational College, Xiamen, Fujian 361100)

“High frequency electronic circuit” is an important course of electronic information major. The amplitude modulation is an important section of the course. This part of the content is difficult to learn, and requires more of the students. In order to explain the profound things in a simple way of teaching, on the basis of summarizing the conventional teaching methods, this paper puts forward a new teaching method, which is based on the conventional teaching, gives the waveform diagram first, and then obtains the expression of the creative teaching method. It is more suitable for the study of the students who are not good at mathematics.

amplitude modulation; creative teaching; higher vocation colleges

2015-12-28

黄文锋(1982-)，男，福建厦门人，厦门海洋职业技术学院信息技术系实验师，硕士。研究方向：电子、通信等相关课程教学与研究。

TN70-4

A

1008-8156(2016)01-0075-03

修回日期：2016-01-25