关于初中数学习题教学的实践探究

朱悦

【摘要】 在初中数学教学中，习题教学是极为重要的构成部分，对培养学生数学思维方式、解题技巧、应用能力等起到极为关键的作用. 本文在阐述初中数学习题教学重要地位及作用的基础上，结合影响其教学效果的主要因素，探究了加强初中习题教学质量的有效实践策略.

【关键词】 初中数学；习题教学；实践探究

引 言

习题教学主要指在课堂教学中，教师为深化学生对所学知识的理解，围绕数学教材习题所开展的一系列教学活动. 在初中课程教学中，数学习题教学是极为重要的一部分，贯穿于数学教学的全过程，对落实素质教学、拓宽学生数学思维、增强学生应用能力起到不可替代的作用. 因此，教师要提高数学教学质量，必须合理组织习题教学实践，充分发挥出数学习题作用对学生的促进作用.

1. 习题在初中数学教学中的地位及作用

数学习题是对教材内容及知识点的总结、提炼以及融会贯通，具备较强的综合性、应用性、启发性以及创新性. 教师通过数学习题教学，将习题解析中应用到的数学思想、数学知识、解题技能等灵活地展示给学生，以帮助初中阶段学生更好地领悟与巩固所学知识，并掌握相关知识应用能力及解题技巧.

2. 影响初中数学习题教学的主要因素

2.1 数学本身特点

初中数学相比于语文、政治等其他课程，具备较为明显的差异性特征，对学生的逻辑思维能力、领悟力以及实践应用能力有着较高要求. 总体而言，数学具有抽象性、准确性以及广泛性三大主要特征. 数学的抽象性主要表现在其概念及验证方法上，其他物理化学家在论断证明方面，往往可借助真实的试验得到结果，而数学家则只能以推理或数据计算的形式进行. 同时，数学定义定理要求必须精准，推理过程严谨及逻辑脉络清晰，而最终获得的数学结论具备无可争议性.

2.2 初中生的认知特点

初中生作为初中数学教学的主体，其认知特点直接影响到习题教学的效果. 在初中阶段的学生，普遍处于青少年时期，生理与心理发育尚未成熟，在课堂教学中往往表现出较强的自我意识，且注意力难以集中，认知能力还有待提升. 在逻辑思维方面，初中生整体表现出较为显著的敏锐性、不成熟性以及可训练性. 因此，教师在习题教学中，应遵循这一阶段学生的认知特征，基于其认知水平开展各项习题教学活动，灵活运用多种教学方法与技巧，调动学生的学习积极性，并为学生留有充足的思考空间，以更好地锻炼其数学思维能力，促进学生的全面发展.

2.3 教师教学水平

教师作为初中数学习题教学活动的组织者、引导者，其教学水平的高低也会对习题教学质量造成极大的影响. 教师的教学水平包括教学经验、教学观念、教学方法等. 教学经验丰富的教师往往能更好地把握教学全局，针对学生心理及学习状态，善于用巧妙、生动的语言、灵活的习题教学内容设计，高效的教学实践活动组织，来达到预期的教学效果. 其中，教师的语言表述能力是极为重要的，由于数学课程本身涉及大量的理论知识、数据分析等，一旦教师以按部就班的形式进行讲解，极易让学生感到枯燥乏味，进而逐渐丧失对数学的学习探索欲望. 因此，初中数学教师在习题教学中，必须考虑到自身因素，不断提升自身教学水平，学会运用语言艺术，以生动、幽默又富有逻辑性的语言来引导学生投入到学习中，共同体验数学习题的解答过程.

3. 提高初中数学习题教学水平的实践探究

3.1 创设情境，探究学习

长期以来，初中数学教师在习题教学中，通常都是照本宣科、就题论题，过于强调对学生课本知识的掌握程度及解题的规范性，而忽视了学生的个性差异，学生在习题教学中难以集中注意力，学习效果不佳. 为此，教师需要改变这种传统的习题教学模式，结合初中生的整体认知特征及个性差异，利用多媒体技术，合理创设情境，将数学习题融入到多样化的问题情境中去，调动学生的探知欲望，通过带有启发性的问题情境设置，来引导学生主动参与教学，开拓思维、积极思考问题隐藏的深意. 同时，增强问题情境的趣味性，激发学生对数学习题的浓厚兴趣.

例如：在一定范围的池塘内，先捕捉50条鱼作出标注，再放回池塘内，待有标注的鱼完全混入到鱼群中去后，开展第二次捕捞行为，所捕鱼数量为200条，其中，带有标注的鱼为10条，以此推测池塘中大概有多少条鱼？此题主要是考查学生对样本估计总体的知识掌握程度，教师可利用多媒体软件，演示池塘内捕鱼推测过程，学生在观察实物图的基础上，能思维更活跃地进行习题解答及演算.

3.2 挖掘隐藏于习题中的数学思想方法

数学思想方法主要指在习题解析过程中，应用到的多种思维方式、解题策略、解题手段、技巧及途径等. 教师在习题教学中，应注重对其题目中隐藏数学思想方法的挖掘，根据初中生的认知特征及知识掌握程度，在科学数学思想的指导下，尝试以多种方法与途径向学生演示习题的解析过程，或鼓励学生进行解题创新，尝试采用新的方法来解答题目，以增强学生的思维创新能力及实践应用能力.

例如，在题目“已知二次函数的图像顶点为（1，-8），并经过点（3，0），求此二次函数解析式. ”教师便可引导学生采取两种解题方法完成题目解答.

解法二：根据题目已给条件，设定解析式为y = a（x - 1）2 - 8，然后再将点（3，0）代入其解析式内，得出0 = a（3 - 1）2 - 8，a = 2，进而得出y = 2（x - 1）2 - 8，y = 2x2 - 4x - 6. 在这一题目解析中，方程思想围绕已知与未知的对立统一关系，既可利用点坐标布列方程组，也可利用顶点式求解.

3.3 构建模型，培养学生应用意识

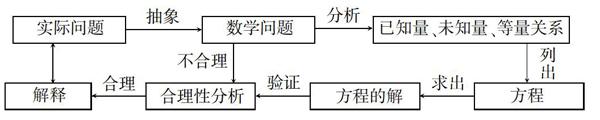
在初中数学习题教学中，教师需考虑到数学本身的抽象性，针对习题构建相应的模型，将解题思路及解题过程具体化，以便于学生更好地分析问题、理清思路，在习题解答中逐步构建完整的知识体系.

例如，题目：某服装店按商品成本价，在提高40%后，又以8折优惠销售，使得每件商品仍可获利15元，求商品的成本价？对于这道习题，教师可构建一元一次方程模型：