“杨辉三角”的拓展探究
“杨辉三角”的拓展探究
◇湖北余智敏1何春玲2
高中数学教材人教A版《选修2-3》中用了较大篇幅介绍“杨辉三角”,主要是因为“杨辉三角”蕴含了丰富的内容,由它可以直观看出二项式定理的性质.杨辉三角是我国古代数学的研究成果之一,它的发现显示了我国古代劳动人民的卓越智慧和才能.
“杨辉三角”将展开式中的二项式系数几何化,使之更加形象地展现在我们眼前.而三项式、四项式、五项式的相应规律却不能用“杨辉三角”来解释.因此,我们的研究还可以继续进行,而要想形象地体现出三项式乃至多项式,也要从数字规律入手.
1多项式系数的代数表示



2多项式系数的几何表示
1)an可理解为一个数轴.数轴、坐标系能够将数据与图形结合,是数与形良好的载体.n无论取何值其“一次项系数”均为1,如图1所示将坐标轴上所有整点赋予“1”.

图1

图2
2) (a+b)n,也可以做出一个坐标系,如图2所示.将x、y轴整点赋予1,而第一象限任意整点上的数等于其左边与下边的数之和.就构成了二项式系数在坐标轴上的排布表.y=-x+1上经过的2点便是(a+b)1的二项式系数.y=-x+2经过的3个点便是(a+b)2的二项式系数,故y=-x+n上的整点数字即为(a+b)n的二项式系数.另外,由于是在坐标轴上,所以每个点就可以表示为naxby(其中n为该点所赋的值,x、y为该点的坐标).
3) 类比以上规律,(a+b+c)n可放入三维坐标系中.用x+y+z=r个平行的面去切割三维坐标系,就会产生一个切面.同样,切面上每个整数点的坐标(x,y,z)表示axbycz,将x、y、z轴整点赋予值1,每个点等于其下面、后面(面对于读者)、左面的3个数之和.
4) (a+b+c+d)n应在四维坐标系中,无法画出.只能推出x+y+z+w=r包含的点代表axbyczdw,无法知道其系数.
3“肩上”规律在三项式中的合情推理
1) 同第2章1)所述,an几何表示仍是直线型.
2) (a+b)n的几何表示就是著名的杨辉三角.如图3所示.其中任一数等于其肩上2数之和.最外侧均为1.第n行即为(a+b)n的二次项系数.第n行第m个数表示an-m+1bm-1的二项式系数,即该数左侧有几个数字就是b的几次方.
1
11
121
1331
14641
15101051
1615201561
172135352171
18285670562881
193684 126 126 843691
11045 120 210 252 210 120 45101
11155 165 330 462 462 330 165 55111
11266 220 495 792 924 792 495 220 66121
图3
3) (a+b+c)n表示为一个四面体.每个侧面都是一个杨辉三角,如图4.不妨将这个四面体一层一层“切开”来看,如图5.将每一层的3条边填入杨辉三角中的对应值,第4层之后中间就开始有点存在了,如图6所示.中间的点等于立体图中其上3个点之和,如6=2+2+2,第5层有12=6+3+3,…以此类推.每个点除了有数字,还要有对应的字母项,如图7.令三角形顶点为a、b、c,三角形中点的某字母的次数就是这个点到该字母对应顶点的对应边所隔线段数.

图4 图5

图6 图7
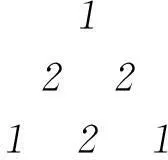
4“肩上规律”的证明
1) 二项式(a+b)n.
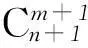
2) 三项式(a+b+c)n.

3) 四项式(a+b+c+d)n.

5其他规律
1) 对称性:二项式(a+b)n的每一层数字左右对称;
三项式(a+b+c)n的每一层的三角形关于三角形中心120°对称;
四项式(a+b+c+d)n的每一层的正四面体关于其中心109°对称(立体对称).
2) 最大值:二项式(a+b)n的每一层最大值为中间1值(或2值);
三项式(a+b+c)n的每一层最大值为中心1值(或3值);
四项式(a+b+c+d)n的每一层最大值为中心1值(或4值).
3) 三项式(a+b+c)n特殊规律:三项式每层呈现边上大,中心小规律,但是查看三角形任一条边(包含三角形内),可以发现这些边都符合杨辉三角某行的数字之比.
证明略.
高中数学教学中关于多项式的数与形的探究可以适当的拓展.以“杨辉三角”为基础,用类比推理的方法拓展至更多变量的情况,并运用代数推理的工具验证这样的推理,便于学生形象地理解多项式,深入地探究多项式的性质,这样能极大地发散他们的思维,引导他们探索学习上的许许多多未知领域.

