定积分计算中原函数求解的简化



定积分计算中原函数求解的简化

◇山东闫西安

定积分的应用是新课标高中数学新增的重要内容,也是与高等数学相衔接的内容,同时该部分与生活实际联系密切,所以成为高考命题的热点问题之一．计算定积分的关键是找准原函数,对于被积函数为常规函数的定积分问题,我们可逆用基本初等函数导数运算求原函数．而对于被积函数为非常规函数的定积分问题,同学们常感无从下手,对此本文提供几种策略,供同学们参考．

1直接利用定积分的几何意义

定积分的几何意义,即求曲边形的面积．对于被积函数较为复杂的定积分问题,若可将被积函数转化为我们所熟悉的平面几何图形,即可利用定积分的几何意义简洁求解．

2利用被积函数的奇偶性

若被积函数是奇函数,则其在对称区间上的定积分为0;若被积函数是偶函数,则其在对称区间上的积分等于正数区间的2倍．利用此性质解题,可达到化难为易、简洁解题．

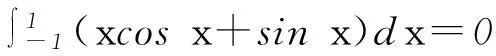
3将被积函数进行等价变形

对于被积函数非常数的积分问题,通过将被积函数进行等价变形,转化为几个常规函数的和或差的形式,再利用定积分的基本运算,分别求定积分．

4逆用复函数求导法则

函数y=f[u(x)]的导数y′=f′[u(x)]u′(x)．如果我们能够把被积函数写成若干个函数之积,而每个函数都是某个函数的导数,则可找到其原函数,再利用微积分基本定理求定积分．

5将被积函数进行等量代换

对于不易直接求原函数的定积分问题,若利用函数图象的对称性,可将其用常规的函数进行代换,则可达到化生为熟的目的．

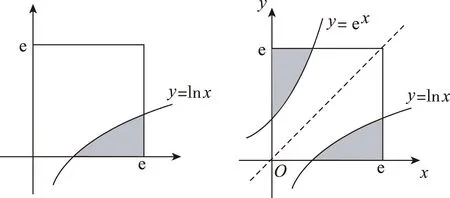
图1　　　　　　　　　　　图2

故答案为1.

6分段讨论求原函数

对于在不同积分区间内具有不同被积函数的定积分问题,可按积分变量所在区间进行分类讨论分别求定积分．

A0;B-4;C19/2;D16

当-2≤x<1时,f(x)=1-x3; 当1≤x≤2时,f(x)=x3-1．所以

故选项为C．

定积分问题中原函数的求解，需要针对不同的情况采用不同的求解方法.希望同学们在学习中不断归纳总结，以提高解此类问题的能力.

(作者单位：山东省定陶县第一中学)