复数高考重点题型及易错点提醒



复数高考重点题型及易错点提醒

◇山东陈静

随着高考改革的不断深入,高考数学中对复数的考查虽然比较基础,有一种一看就会的感觉,但是如果思考不细心就会在某方面出现差错.现将复数高考重点题型及易错点提醒总结如下,以帮助同学们进一步提升解题技能.

1考查复数的基本概念

A充分非必要条件;

B必要非充分条件;

C充要条件;

D既非充分又非必要条件

错解设z1=2+i, z2=1-i,则z1-z2=1+2i,得到当z1、z2中至少有1个数是虚数,z1-z2一定是虚数，即充分性成立.容易判断必要性成立.故选C.

正解若z1、z2皆是实数,则z1-z2一定不是虚数,因此当z1-z2是虚数时,则“z1、z2中至少有1个数是虚数”成立,即必要性成立;当z1、z2中至少有1个数是虚数,z1-z2不一定是虚数,如z1=z2=i,即充分性不成立.故选B.

易错点提醒本题目易错点在于首先要分清复数的有关概念,形如a+bi(a、b∈R)的数叫复数,其中a、b分别是它的实部和虚部.若b=0,则a+bi为实数;若b≠0,则a+bi为虚数;若a=0且b≠0,则a+bi为纯虚数.判断概念必须从其定义出发,在判断充分性是否成立时往往会忽略了2个虚数相等时差是实数的情况,因此在审题中要细心严谨.

2考查复数的基本运算

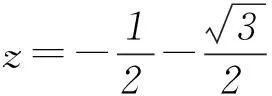
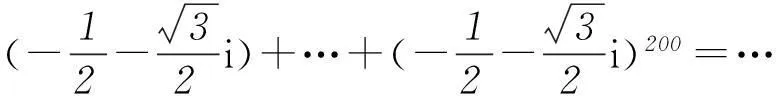
计算烦琐,思路受阻.

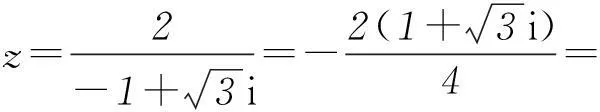
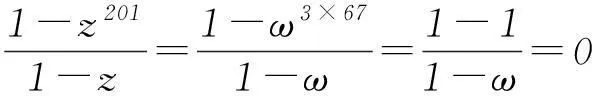
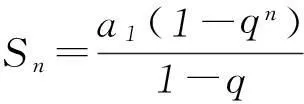
3考查复数的几何意义

A椭圆;B线段;

C圆;D无轨迹

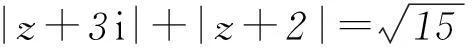
变式(2015年陕西卷)设复数z=(x-1)+yi (x、y∈R)，若|z|≤1，则y≥x的概率为().

A 34+12π; B 14-12π;

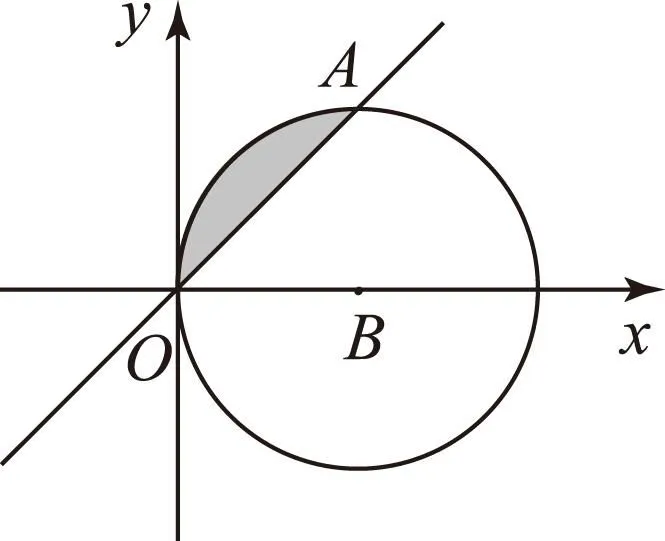
图1

如图可求得A(1,1),B(1,0),阴影面积为

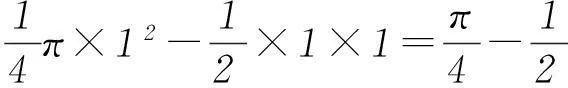
4考查复数的综合应用

错解化简求ω=2-i,z1=3+i,故另一个根是z2=-3+i,所求的一个一元二次方程可以是

x2-2ix-10=0.

正解因为ω(1+2i)=4+3i, 所以

易错点提醒在由已知条件确定ω时的2种方法代数化和分母实数化都可以解决,但要细心运算,最容易出错的方面就是实系数方程有虚根则虚根成对出现，这一结论不能疏忽，否则就无法确定方程.

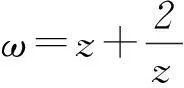
-4<ω<1.

求|z|的值及z的实部的取值范围.

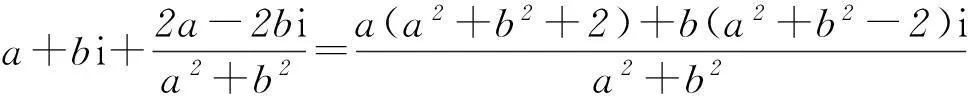
总之,复数部分高考题一般较容易,主要考查复数的基本概念、基本运算、复数的几何意义以及复数的综合应用.只要在运算中做到细心、认真,关注知识交会方面的灵活处理,那么复数问题就会迎刃而解.

(作者单位：山东省平度经济开发区高级中学)